模型2:CAC rule 只要这个条件满足,就可以给出一个合理的 M + 1+v 功率分配方案,使得所有用户的SNR都满足 要求。 ◆一个呼叫请求到达时,若下式满足,则可以接纳该请求: 1+1+r 注意,使用上述CAC规则存在两个条件: One Class of Calls 2Spatially Homogeneity Assumption 2020年秋季 16/60 无线互联网
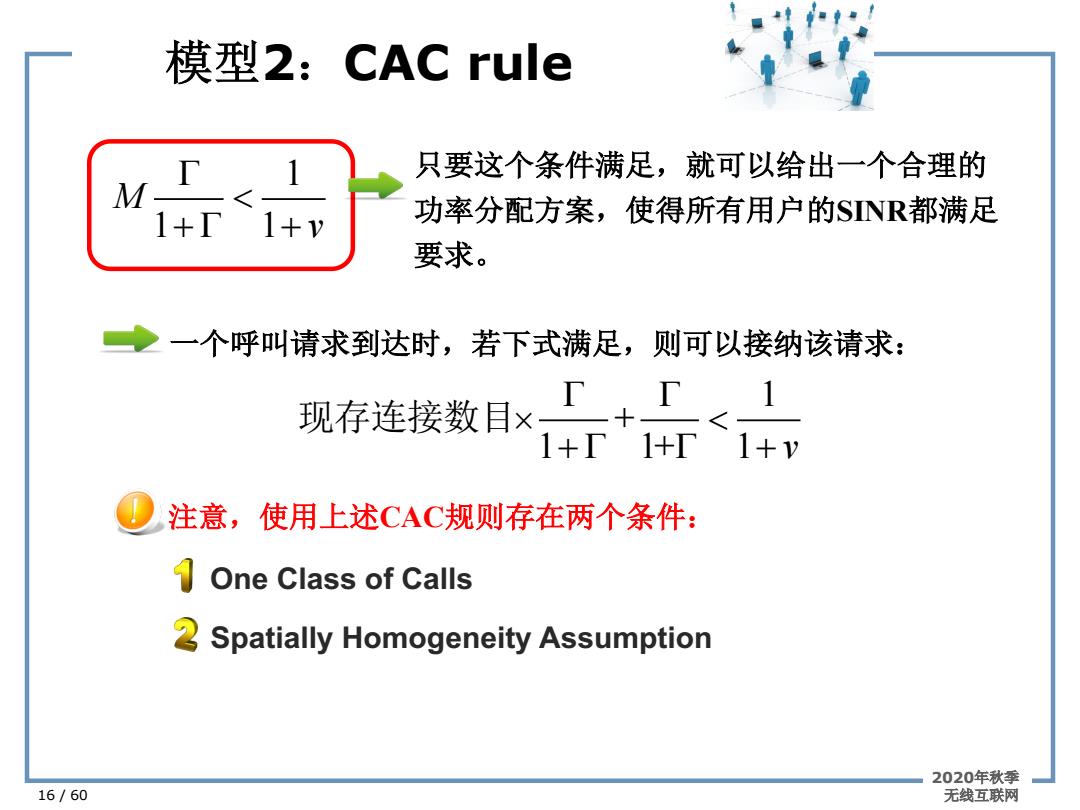
模型2:CAC rule 16 / 60 1 1 1 M v G < + G + 只要这个条件满足,就可以给出一个合理的 功率分配方案,使得所有用户的SINR都满足 要求。 一个呼叫请求到达时,若下式满足,则可以接纳该请求: 1 + 1 1+ 1 v G G ´ < + G G + 现存连接数目 注意,使用上述CAC规则存在两个条件: One Class of Calls Spatially Homogeneity Assumption 2020年秋季 无线互联网
模型2:“用户需求” 为了达到一定的误码率要求, 物理层硬件需要的最低信噪比。 CDMA系统的处理增益:RcJR 以IS95为例: IS95的物理层技术保证了,只要Y=6dB,即可使得9.6kbps的常用 话音编解码器正确接收话音。 四IS95中,系统带宽为1.25MHz,chip rate为R。=1.2288Mcps。 ◆处理增益为:1.2288×106/9.6×103=128兰21dB ◆T=6-21=-15dB÷1/32 GSM系统中,目标SINR约为8~10dB。 2020年秋季 17/60 无线互联网
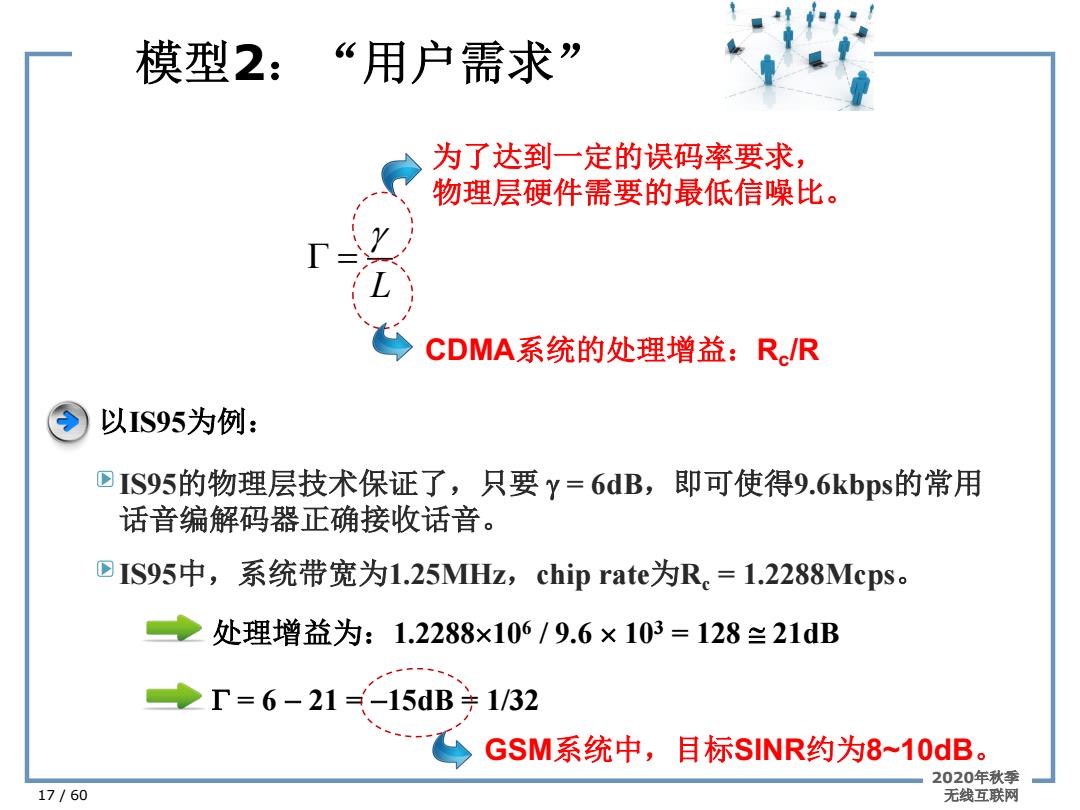
模型2:“用户需求” 17 / 60 L g G = 为了达到一定的误码率要求, 物理层硬件需要的最低信噪比。 CDMA系统的处理增益:Rc/R 以IS95为例: IS95的物理层技术保证了,只要 g = 6dB,即可使得9.6kbps的常用 话音编解码器正确接收话音。 IS95中,系统带宽为1.25MHz,chip rate为Rc = 1.2288Mcps。 处理增益为:1.2288´106 / 9.6 ´ 103 = 128 @ 21dB G = 6 - 21 = -15dB = 1/32 GSM系统中,目标SINR约为8~10dB。 2020年秋季 无线互联网

模型2:“系统资源” 从上面的讨论中,可以看出,“系统资源”11+) 的概念是从本区上行功率Q和邻区干扰Q这两个概念 经数学推导得到的。 ?没人觉得别扭吗? NOISE or PHILOSOPHY 四这是工程科学中比较罕见的例子:先于物理直觉的 数学推导。 四另一个例子是:等效带宽。 以可理解的方式建模现实问题的强烈愿望。 四一定要小心(以太的例子)。 2020年秋季 18/60 无线互联网
模型2:“系统资源” 18 / 60 从上面的讨论中,可以看出,“系统资源”1/(1+v) 的概念是从本区上行功率Q和邻区干扰vQ这两个概念 经数学推导得到的。 2020年秋季 无线互联网 没人觉得别扭吗? NOISE or PHILOSOPHY 这是工程科学中比较罕见的例子:先于物理直觉的 数学推导。 另一个例子是:等效带宽。 以可理解的方式建模现实问题的强烈愿望。 一定要小心(以太的例子)

模型2:VAD 从物理意义上看,干扰值O减小,系统容量也可以增大。 ◆减少O值的简单方法:VAD(Voice Activity Detection) ◆ 考虑该因素,相当于引入一个参数, 称为voice activity factor。 系统资源:1/(u(1+) 参数u的通常取值为0.40.5 若考虑VAD,则系统容量可以提高2~2.5倍。 2010年春季 19/60 宽带网的性能分析与优化设计
模型2:VAD 2010年春季 19 / 60 宽带网的性能分析与优化设计 从物理意义上看,干扰值Q减小,系统容量也可以增大。 减少Q值的简单方法:VAD(Voice Activity Detection) 考虑该因素,相当于引入一个参数u, 称为voice activity factor。 系统资源:1/ (u(1+v)) 参数u的通常取值为0.4~0.5 若考虑VAD,则系统容量可以提高2~2.5倍
功率比值V=? 模型2的讨论中,有一个关键的参数:本区上行功率Q与邻区干扰总和 之间的比值。 真实网络环境中,这个值到底是多少? 推导思路: 硬切换: 四仍然假定所有MS在空间上均匀分布: MS由离他最近 ◆只要得到单个坐标点上MS的千扰公式, 的BS提供服务。 按面积求积分即可得到总的干扰。 软切换: 国传播模型中增加了对阴影效应的考虑; MS由信道质量 ◆放弃前面的假设:传播损耗只跟距离相关。 最好的BS提供 服务。 ⊙分别讨论软切换策略和硬切换策略; 什么时候最近的 更精确地考虑MS与BS之间的关联关系。 BS反而信道质量 不好? 2020年秋季 20/60 无线互联网
功率比值 v = ? 20 / 60 模型2的讨论中,有一个关键的参数 v:本区上行功率Q与邻区干扰总和 之间的比值。 真实网络环境中,这个值到底是多少? 推导思路: 仍然假定所有MS在空间上均匀分布; 传播模型中增加了对阴影效应的考虑; 分别讨论软切换策略和硬切换策略; 只要得到单个坐标点上MS的干扰公式, 按面积求积分即可得到总的干扰。 放弃前面的假设:传播损耗只跟距离相关。 更精确地考虑MS与BS之间的关联关系。 硬切换: MS由离他最近 的BS提供服务。 软切换: MS由信道质量 最好的BS提供 服务。 什么时候最近的 BS反而信道质量 不好? 2020年秋季 无线互联网