
定理2.1.1度量空间(X,p)的球 形邻域具有以下基本性质: >每一点x∈X至少有一个球形邻域, 并且点x属于它的每一个球形邻域: >对于点x∈X的任意两个球形邻域,存 在x的一个球形邻域同时包含于两者. 11
11 定理 2.1.1 度量空间 ( , ) X 的球 形邻域具有以下基本性质: ➢每一点x∈X 至少有一个球形邻域, 并且点 x 属于它的每一个球形邻域. ➢对于点 x∈X 的任意两个球形邻域, 存 在 x 的一个球形邻域同时包含于两者. 定理 2.1.1 度量空间 ( , ) X 的球 形邻域具有以下基本性质: ➢每一点x∈X 至少有一个球形邻域, 并且点 x 属于它的每一个球形邻域. ➢对于点 x∈X 的任意两个球形邻域, 存 在 x 的一个球形邻域同时包含于两者. 定理 2.1.1 度量空间 ( , ) X 的球 形邻域具有以下基本性质: ➢每一点x∈X 至少有一个球形邻域, 并且点 x 属于它的每一个球形邻域. ➢对于点 x∈X 的任意两个球形邻域, 存 在 x 的一个球形邻域同时包含于两者
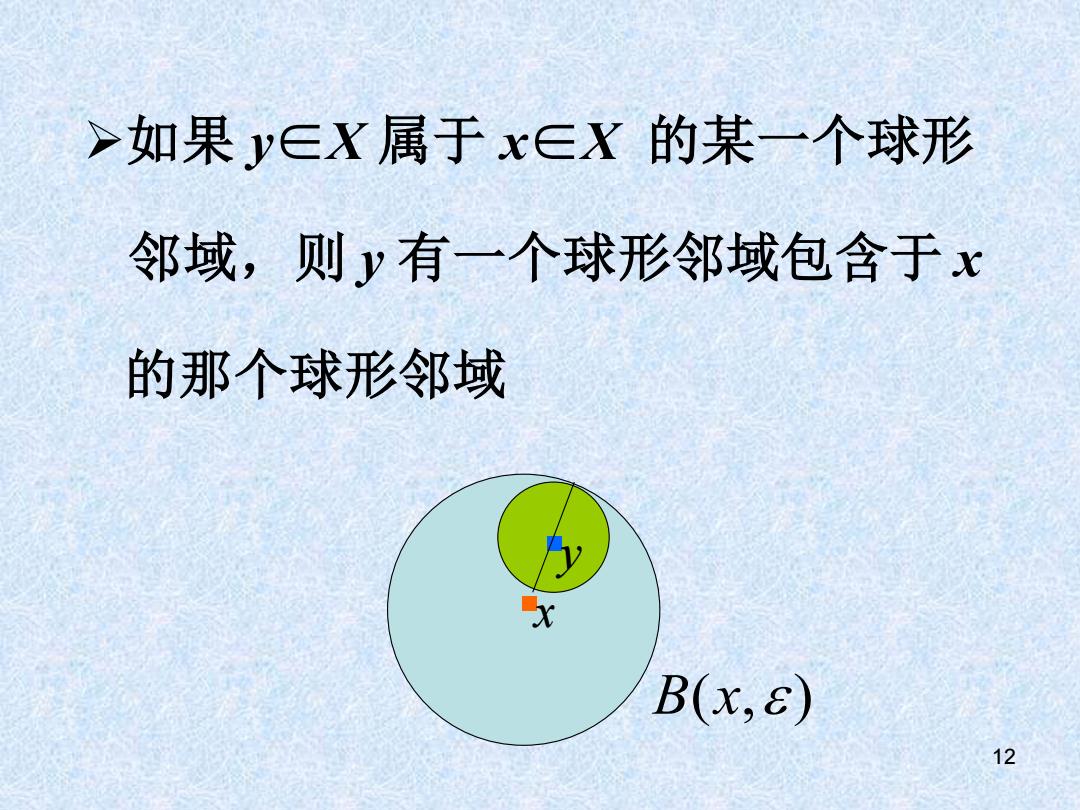
>如果y∈X属于x∈X的某一个球形 邻域,则y有一个球形邻域包含于x 的那个球形邻域 B(x,s) 12
12 ➢如果 y∈X 属于 x∈X 的某一个球形 邻域,则 y 有一个球形邻域包含于 x 的那个球形邻域 .x .y B x( , )