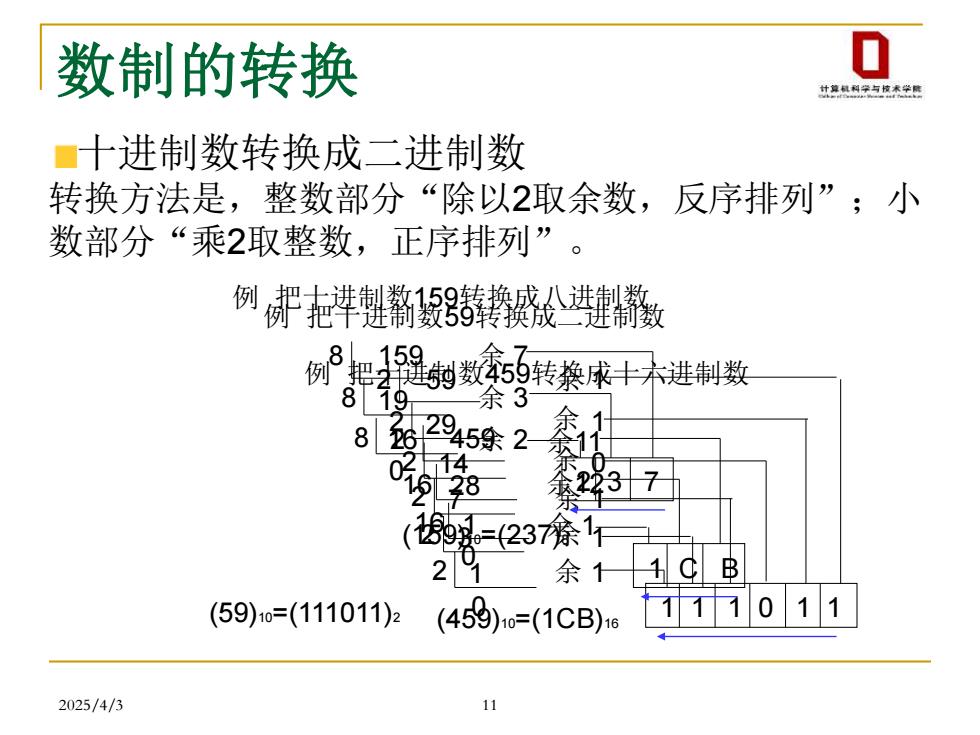
数制的转换 0 计草机利学与校术学网 ■十进制数转换成二进制数 转换方法是,整数部分“除以2取余数,反序排列”;小 数部分“乘2取整数,正序排列”。 例魁翦静成 把牛进箭数$转换战进箭数 3起制数转袋宋十木进制数 819 —余3 82 2952 4 37 (-237徐11 21 余11GB (59)0=(111011)2 (458)=(1CB)611011 2025/4/3 11
2025/4/3 11 十进制数转换成二进制数 转换方法是,整数部分“除以2取余数,反序排列”;小 数部分“乘2取整数,正序排列”。 例 把十进制数59转换成二进制数 2 59 2 29 2 14 2 7 2 3 2 1 (59)10=(111011)2 0 1 1 0 1 1 1 1 1 1 0 1 1 余 余 余 余 余 余 例 把十进制数159转换成八进制数 8 159 8 19 8 2 0 (159)10=(237)8 2 3 7 余 7 余 3 余 2 例 把十进制数459转换成十六进制数 16 459 16 28 16 1 0 (459)10=(1CB)16 1 C B 余11 余12 余 1 数制的转换

数制的转换 0 什草凤利学与拉未学脑 例如:将十进制小数0.625转换成二进制数 用乘2取整法,转换过程如下: 0.625×2=1.25 取出整数1(最高位) 0.25×2=0.5 取出整数0↓ 0.5×2=1.0 取出整数1(最低位) 即0.625=0.101B 注意:有的十进制小数不能用二进制小数精确地表示出 来
数制的转换 例如:将十进制小数0.625转换成二进制数 用乘2取整法,转换过程如下: 0.625×2=1.25 取出整数 1 (最高位) 0.25×2=0.5 取出整数 0 ↓ 0.5×2=1.0 取出整数 1 (最低位) 即0.625 =0.101B 注意:有的十进制小数不能用二进制小数精确地表示出 来

数制的转换 计草机利学与校未学网 ,二进制、八进制、十六进制数转换为十进数 对于任意一个二进制数、八进制数、十六进制,可以 写出它的按权展开式,再相加求和即可 例如: (1111.11)2=1×23+1×22+1×21+1×20+1×2-1 +1×2-2=15.75 (A10B.8)16=10×163+1×162+0×161+11×160 +8×161=41227.5
数制的转换 ◼ 二进制、八进制、十六进制数转换为十进数 对于任意一个二进制数、八进制数、十六进制,可以 写出它的按权展开式,再相加求和即可 例如: (1111.11)2= 1×2 3+1×2 2+1×2 1+1×2 0 +1×2 -1 +1×2 -2=15.75 (A10B.8)16=10×163+1×162+0×161+11×160 +8×16-1= 41227.5

数制的转换 0 什草凤利学与拉未学脑 ·二进制数与八进制数的相互转换 二进制数转换成八进制数的方法是“三位合一位”法。 例如将11111101.101转换成八进制数: 011111101.101 ↓ ↓ ↓ ↓ 3 75.5 转换结果为11111101.101B=375.5Q。 八进制数转换成二进制数方法,正好与二进制数转换 成八制数的方法相逆,即“一位扩展三位”法
数制的转换 ◼ 二进制数与八进制数的相互转换 二进制数转换成八进制数的方法是“三位合一位”法。 例如 将11111101.101转换成八进制数: 011 111 101 . 101 ↓ ↓ ↓ ↓ 3 7 5 . 5 转换结果为11111101.101B = 375.5Q。 八进制数转换成二进制数方法,正好与二进制数转换 成八制数的方法相逆,即“一位扩展三位”法

0 计草机利学与校未学网 ■例如将246.45Q转换成二进制数 2 4 6, 4 5 ↓ ↓ ↓ 010100110.100 101 ■转换结果为246.45Q=010100110.100 101B
◼ 例如 将246.45Q转换成二进制数 2 4 6 . 4 5 ↓ ↓ ↓ ↓ ↓ 010 100 110 . 100 101 ◼ 转换结果为246.45Q = 010100110 .100 101 B