
树的性质的“极限性” a)Every edge of a tree is a cut-edge. b)Adding one edge to a tree forms exactly one cycle. c)Every connected graph contains a spanning tree. 间题4: 什么样的图生成树是唯一的,为什么?
树的性质的“极限性

关于树的另外一个性质 Theorem 4.9 Let T be a tree of order k.If G is a graph withδ(可≥k-1,then T is isomorphic to some subgraph of G
关于树的另外一个性质 Theorem 4.9 Let T be a tree of order k. If G is a graph with δ(G) ≥ k − 1, then T is isomorphic to some subgraph of G

如何构造一个连通图的生成树?
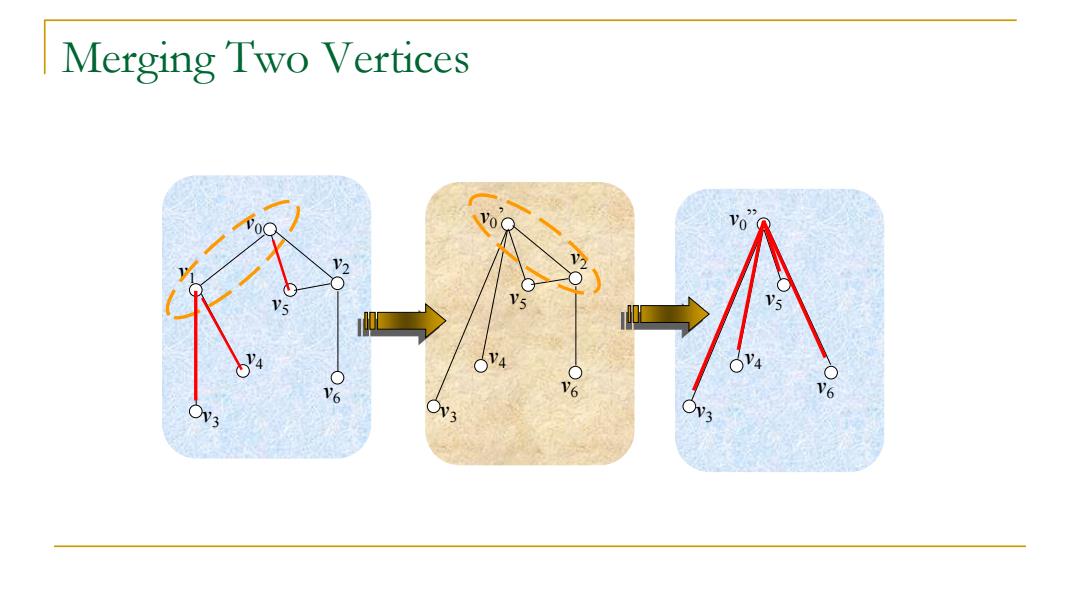
Merging Two Vertices V6
Merging Two Vertices v0 v6 v2 v5 v4 v1 v3 v6 v2 v5 v4 v3 v0 ’ v6 v5 v4 v3 v0
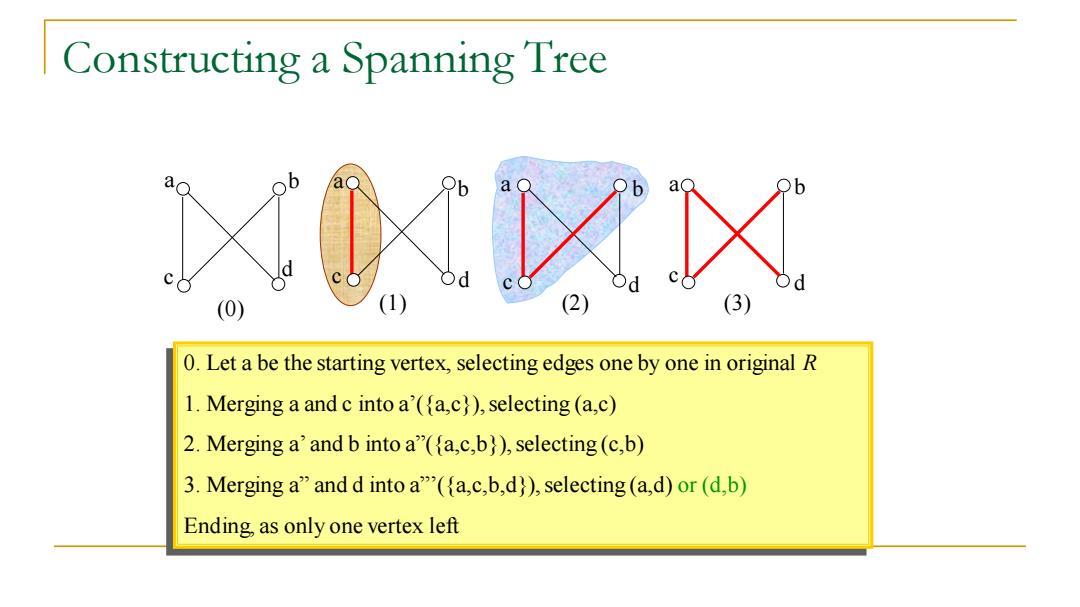
Constructing a Spanning Tree a a 1 0.Let a be the starting vertex,selecting edges one by one in original R 1.Merging a and c into a'(fa,c)),selecting (a,c) 2.Merging a'and b into a"(fa,c,b)),selecting (c,b) 3.Merging a"and d into a"(a,c,b,d)),selecting (a,d)or(d,b) Ending,as only one vertex left
Constructing a Spanning Tree a b c d a b a b a b c c d c d d 0. Let a be the starting vertex, selecting edges one by one in original R 1. Merging a and c into a’({a,c}), selecting (a,c) 2. Merging a’ and b into a”({a,c,b}), selecting (c,b) 3. Merging a” and d into a”’({a,c,b,d}), selecting (a,d) or (d,b) Ending, as only one vertex left (0) (1) (2) (3)