
问题6: 我们有什台办法来应对这种 情况? f1=1;f2=1; 输出f1,f2; for(i=3;i<n,i++) 你有启发吗? f3=f1+f2; 输出f3; f1=f2;f2=f3;
f1=1;f2=1; 输出f1,f2; for(i=3;i<n,i++){ f3=f1+f2; 输出f3; f1=f2;f2=f3; } 你有启发吗?
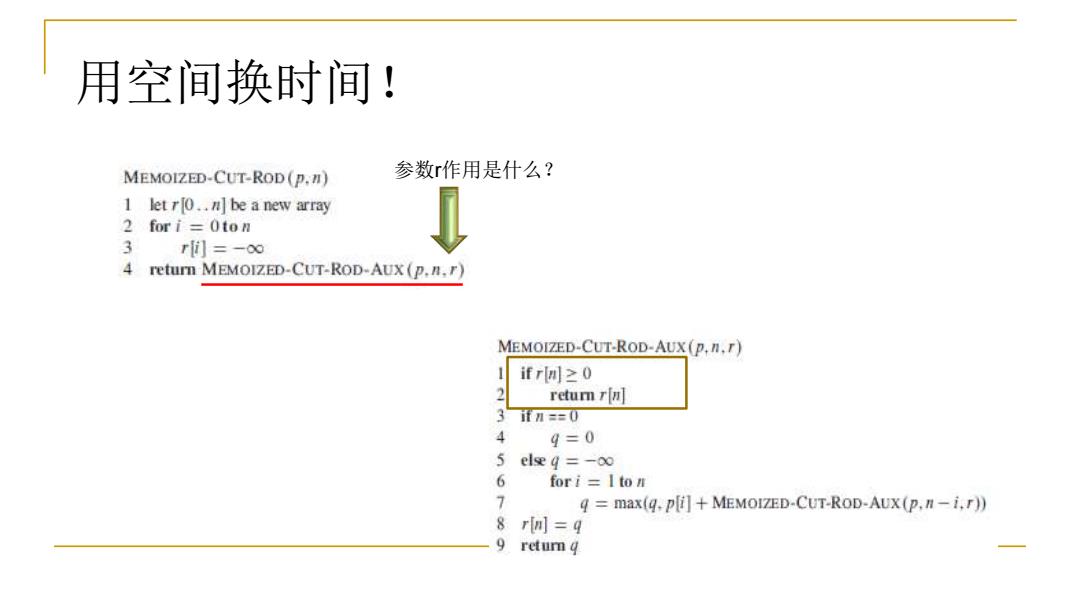
用空间换时间! MEMOIZED-CUT-ROD (P.) 参数r作用是什么? 1 let r0..n]be a new array 2 for i =Oton 3 r刊=-o∞ 4 return MEMOIZED-CUT-ROD-AUX (p.n.r) MEMOIZED-CUT-ROD-AUX(p.n.) ifr间≥0 2 retur rn] 3if刀==0 4 9=0 5eleg=-o∞ 6 fori I to n 7 g max(g.p[i]MEMOIZED-CUT-ROD-AUX(p,n-i,r)) 8 rin]=q 9 return q
参数r作用是什么? 用空间换时间!
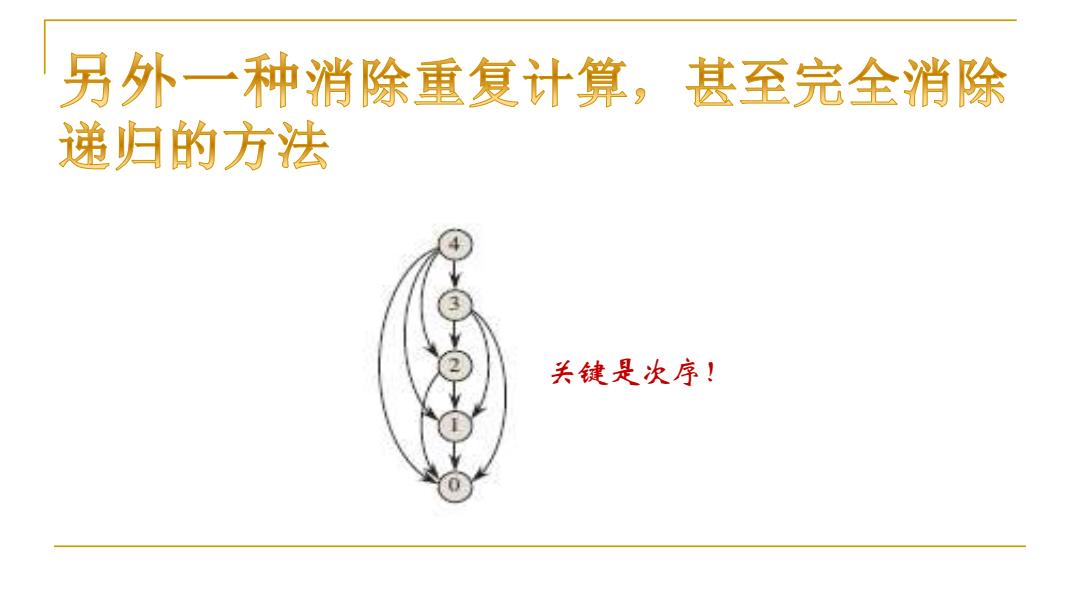
另外一种消除重复计算,甚至完全消除 递归的方法 关键是次序!
关键是次序!

子问题的序在动态规划算法设计中非常重要: BOTTOM-UP-CUT-ROD(P.m) 1 let r[0..n]be a new array 2 rO1=0 3 forj I to n 请结合代码解释 4 9=-00 “序”的体现! 5 fori I toj 6 q max(g.pli]+rli-i]) 7 ru]=q 8 retum rn]
子问题的序在动态规划算法设计中非常重要: 请结合代码解释 “序”的体现!

上面两种方法,均将递归版动态规划中重复计 算消除了。两者有什么共同点? 你能否解释我们的前辈为什么用d心ynamic programming来命名这个方法?