
更关键的是:我们从公式中的ri 求解中,看到了什么? In Tn=ri+rn-i 递归!
rn : i rn =ri+rn-i 递归!

递归的解法:扫描所有可能的割法 In max (Pn,rI In-1,r2 +In-2,...,In-1+r1) max (Pi+rn-i) <i<刀 Cut-Rod(p,n){ P:价格表,n:长度 if n==0 return 0; q=-1; for(i=1 to n){ ∥递归遍历所有的“割法” q max(q,p[i]+Cut-Rod(p,n-i)) return q;
递归的解法:扫描所有可能的割法 Cut-Rod(p,n) { //P:价格表,n:长度 if n==0 return 0; q=-1; for( i=1 to n) { //递归遍历所有的“割法” q = max(q, p[i]+Cut-Rod(p, n-i)) } return q; }
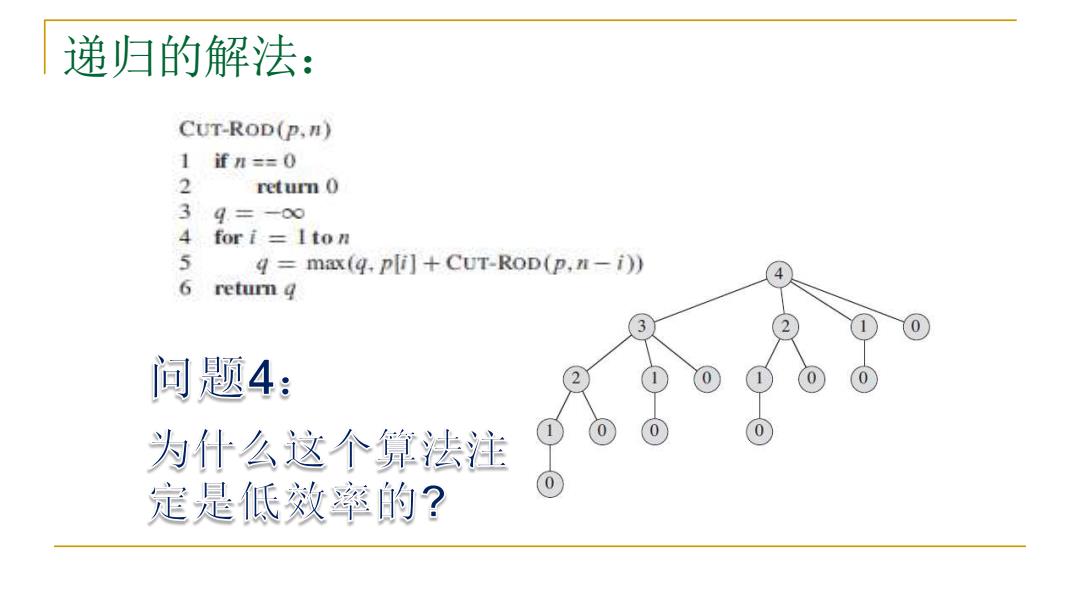
递归的解法: CUT-ROD(P.n) 1fn==0 2 return 0 3q.=-00 4 for i Iton 5 4 max(g.pli]+CUT-ROD(p,n-i)) 6 return q 3 0 问题4: 为什么这个算法注 定是低效率的?
递归的解法:

Fibonacci:F=F+Fn2 间题5: 如果要你计算第n个 Fibonacci数,你用递归还是 用循环,还是随便?为什么?
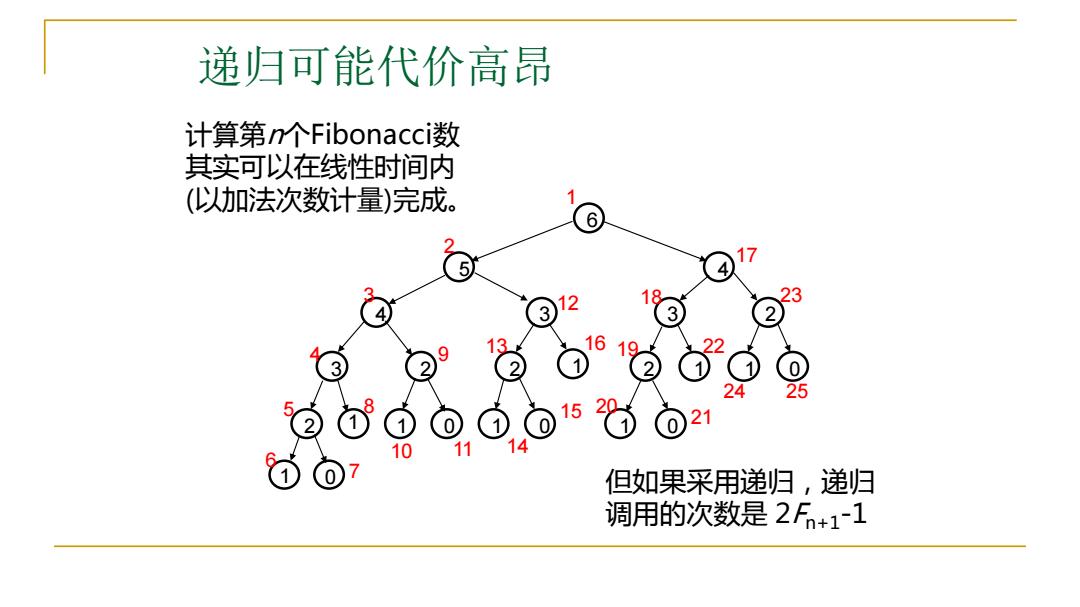
递归可能代价高昂 计算第n个Fibonacci数 其实可以在线性时间内 (以加法次数计量)完成。 1 6 5 4 18 23 4 3 12 3 13 16 9 9 2 25 10 但如果采用递归,递归 调用的次数是2Fn+1~1
递归可能代价高昂 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 2 4 3 3 3 6 5 4 13 16 10 11 9 8 12 3 4 5 6 7 14 15 21 2 1 19 18 17 25 23 24 22 20 计算第n个Fibonacci数 其实可以在线性时间内 (以加法次数计量)完成。 但如果采用递归,递归 调用的次数是 2Fn+1-1