
Framework and Assumptions Case I:X is nonstochastic Questions: What happens to Assumption 3.2 if X is nonstochastic? If X is nonstochastic,Assumption 3.2 becomes E(et X)=E(et)=0. An example of nonstochastic X is Xt=(1,t,..,t)',where t is a time variable.This corresponds to a time-trend regression model Y:=XtB°+et 5-039+e6. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 11
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 11 Framework and Assumptions Case I: X is nonstochastic Questions:

Framework and Assumptions Case ll:{=(Yt,X1 is an IID random sample .When {Zt}is IID,Assumption 3.2 becomes E(et X)= E(et X1,X2,...Xt;...,Xn) E(et X:) 0. Assumption 3.3 [Nonsingularity]: (a)The minimum eigenvalue of the KxK square matrixX'X=XX is nonsingular,and (b)with probability one, λmin(X'X)→oasn→o. Assumption 3.3(a)rules out multicollinearity among the (k+1)regres- sors in Xt.Multicollinearity refers to a situation in which two or more explanatory variables in a multiple regression model are linearly related. To be continued ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 12
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 12 Framework and Assumptions Case II: is an IID random sample Assumption 3.3 To be continued

Framework and Assumptions Formally,we say that there exists multicollinearity or perfect multicollinear- ity among the Xt if for all te {1,...,n},the variable Xit for some j{0,1,...,k}is a linear combination of the other K-1 column variables Xit,ij.In this case,the matrix X'X is singular,and as a result,the true model parameter Bo in Assumption 3.1 is not identifiable. The nonsingularity of X'X implies that X must be of full rank of K=k+1. Thus,we need K <n.That is,the number of regressors cannot be larger than the sample size.This is a necessary condition for identification of parameter B°. The eigenvalue A of a square matrix A is characterized by the system of linear equations: det(A-λI)=0, where det()denotes the determinant of a square matrix,and I is an identity matrix with the same dimension as A. To be continued ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 13
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 13 Framework and Assumptions To be continued

Framework and Assumptions It is well-known that the eigenvalue A can be used to summarize infor- mation contained in a matrix (recall the popular principal component analysis).Assumption 3.3 implies that new information must be available as the sample size n-oo (i.e.,Xt should not only have same repeated values as t increases). Intuitively,if there are no variations in the values of the Xt,it will be difficult to determine the relationship between Yt and Xt (indeed,the purpose of classical linear regression is to investigate how a change in X causes a change in Y).In certain sense,one may call X'X the "information matrix"of the random sample X because it is a measure of the informa- tion contained in X.The magnitude of X'X will affect the preciseness of parameter estimation for Bo. -Indeed,as will be shown,the condition that Amin(X'X)→oasn→∞ ensures that variance of the OLS estimator will vanish to zero as n- oo.This rule out a possibility called near-multicollinearity that there is an approximate linear relationship among two or more explanatory variables such that although X'X is nonsingular,its minimum eigenval- ue Amin(X'X)does not grow with the sample size n.When Amin(X'X) does not grow with n,the OLS estimator is well-defined and has a well- behaved finite sample distribution,but its variance never vanishes to zero asn→oo. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 14
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 14 Framework and Assumptions
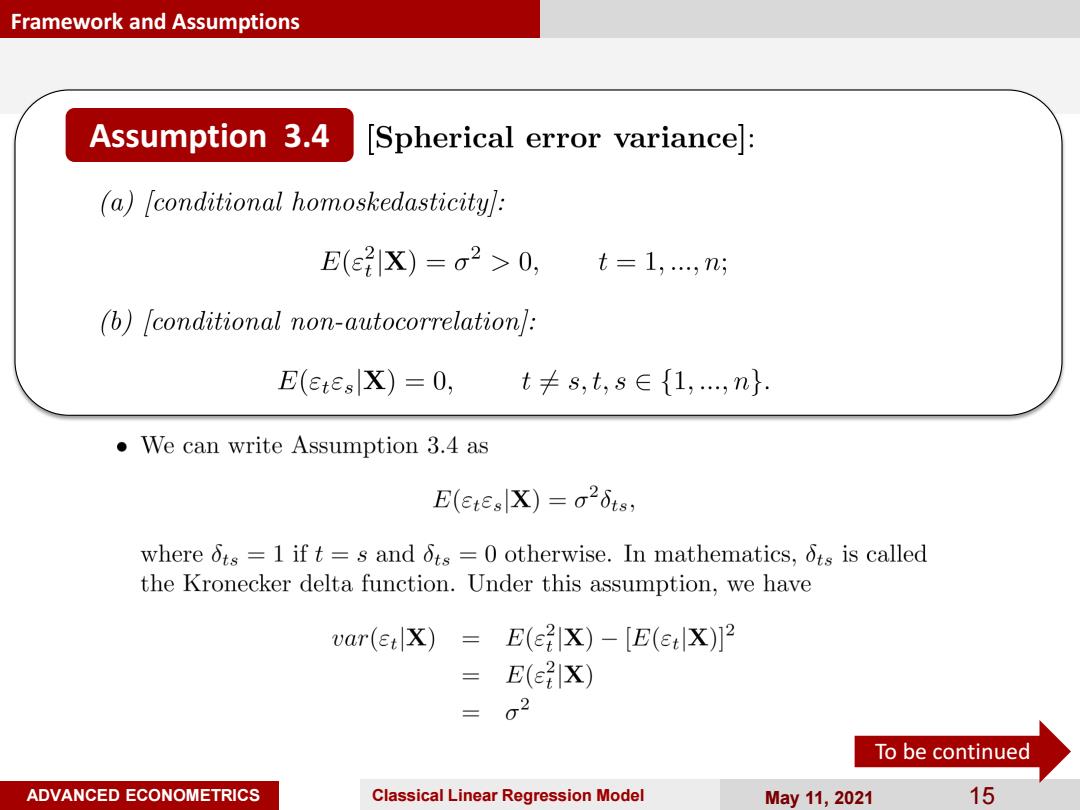
Framework and Assumptions Assumption 3.4 [Spherical error variancel: (a)[conditional homoskedasticity: E(eX)=o2>0,t=1,,n (b)fconditional non-autocorrelation: E(EtEs X)=0, t≠s,t,s∈{1,,n. We can write Assumption 3.4 as E(etes|X)=0261s, where 6ts =1 if t=s and 6ts =0 otherwise.In mathematics,Ots is called the Kronecker delta function.Under this assumption,we have var(Ei X) =E(e?X)-E(et X)2 E(e x) g2 To be continued ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 15
ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 15 Framework and Assumptions Assumption 3.4 To be continued