
2 二项分布的性质: P(X=x)=P (x) (x=0,1,.,n) 二项分布的概率之和等于1,即 Cp(1-p)”-=1 x三0 P(X≤m)=P(x≤m)=∑Cp(1-p)- P(X≥m)=Pn(x≥m)=∑C (1-0) x=m P(m,≤X≤m,)=p.(m,≤x≤m,)=∑Cp(1-p)胖 (ml≤m2)
0 ( )( ) 1 m n x x x n n x PX m P x m C ( )( ) 1 n n x x x n n x m PX m P x m C 2 1 1 2 12 ( )( ) 1 m n x x x n n x m Pm X m p m x m C (m1<m2) P(X=x)=P (x)(x=0,1,.,n) 二项分布的概率之和等于 二项分布的概率之和等于1,即 0 (1 ) 1 n x x nx n x C 2. 二项分布的性质: 二项分布的性质:
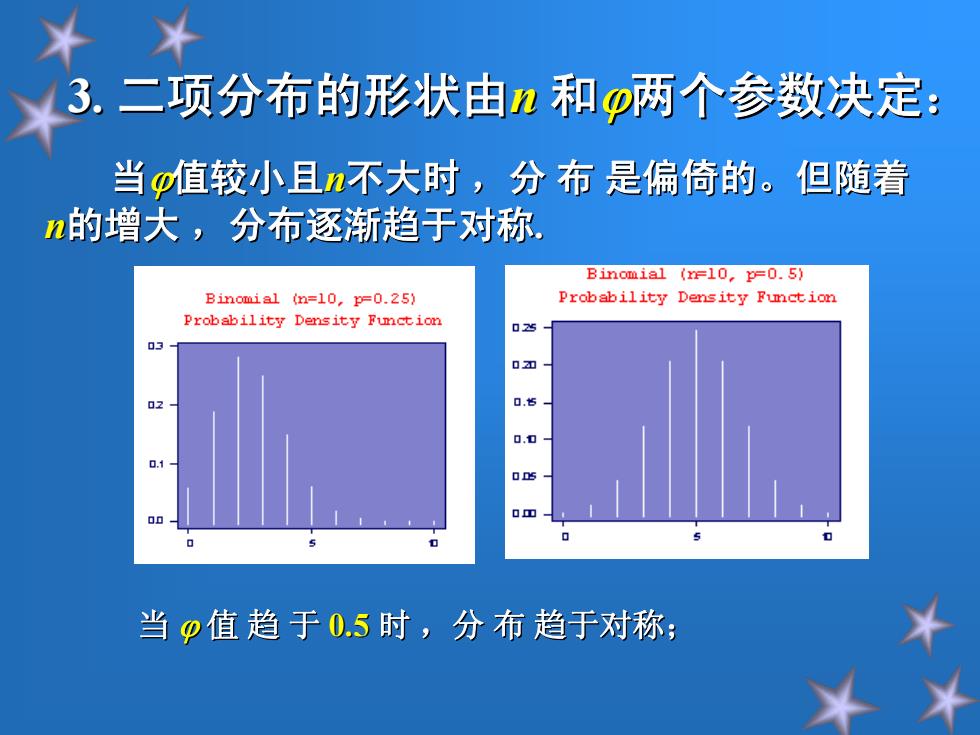
3.三项分布的形状由n和p两个参数决定: 当p值较小且n不大时,分布是偏倚的。但随着 n的增大,分布逐渐趋于对称 Binomial (rF10,p=0.5) Binomial (n=10,p=0.25) Probability Density Fuction Probability Density Fumction 025 03 02 当p值趋于0.5时,分布趋于对称:
3. 二项分布的形状由 二项分布的形状由n 和两个参数决定: 两个参数决定: 当值较小且n不大时 ,分 布 是偏倚的。但随着 是偏倚的。但随着 n的增大 ,分布逐渐趋于对称 ,分布逐渐趋于对称. 当 值 趋 于 0.5时 ,分 布 趋于对称;
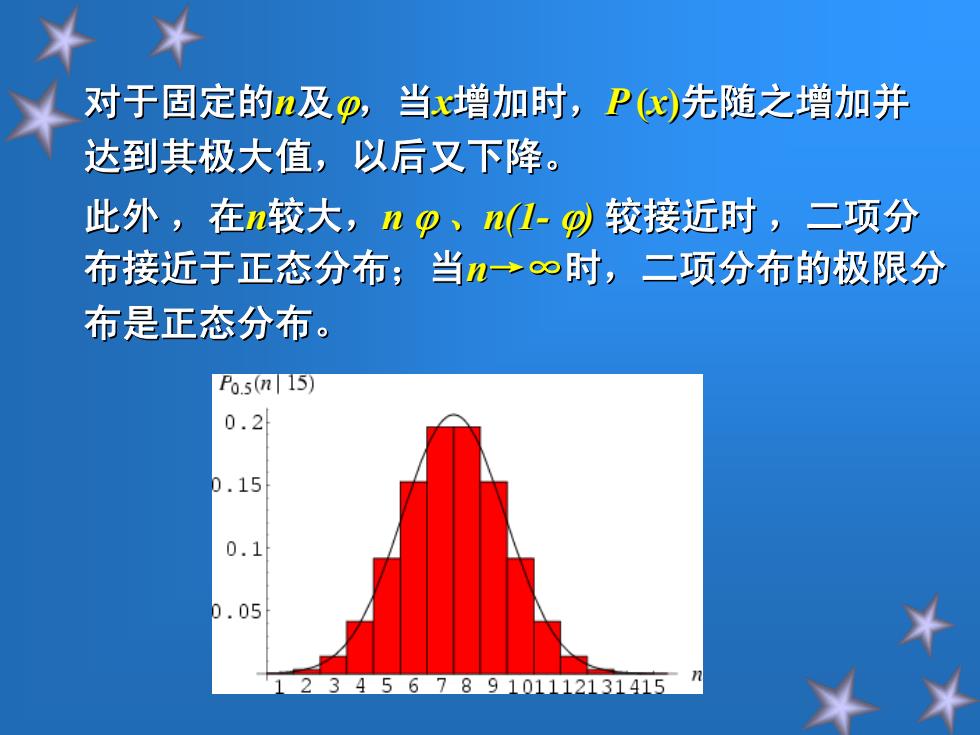
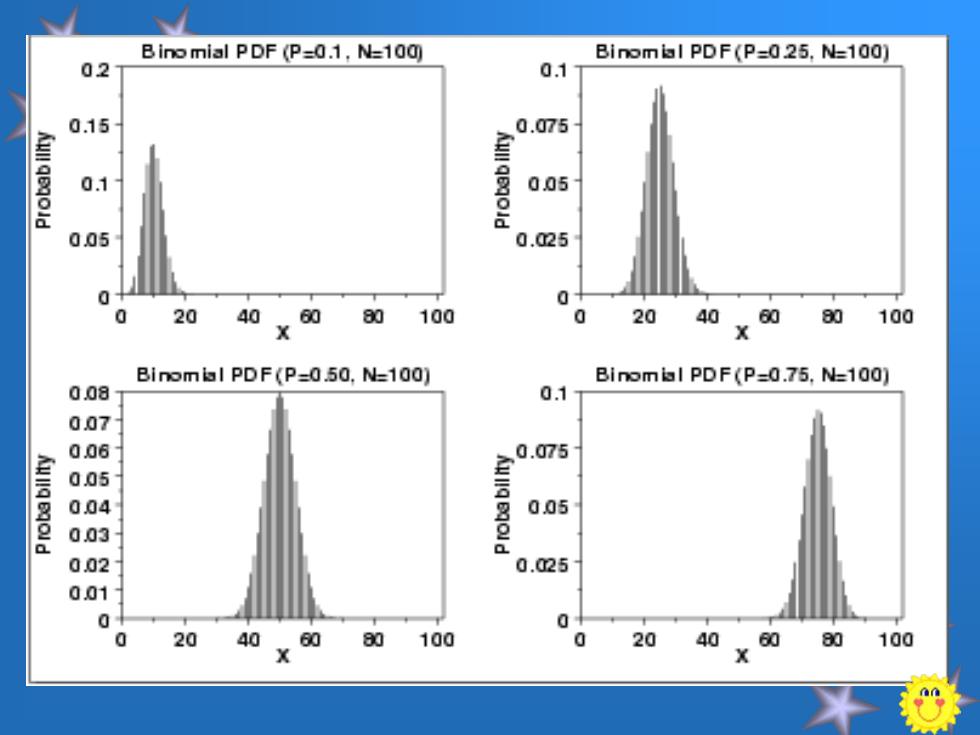
对于固定的n及p,当x增加时,Px)先随之增加并 达到其极大值,以后又下降。 此外,在n较大,np、n1-到较接近时,二项分 布接近于正态分布;当n→∞时,二项分布的极限分 布是正态分布。 Fo.5n15) 0.2 D.15 0.1 0.05 3456789101112131415
对于固定的n及,当x增加时,P(x)先随之增加并 达到其极大值,以后又下降。 达到其极大值,以后又下降。 此外 ,在n较大,n 、n(1-)较接近时 ,二项分 布接近于正态分布;当 布接近于正态分布;当 n→∞时,二项分布的极限分 时,二项分布的极限分 布是正态分布。 布是正态分布
Bino mial PDF (P=0.1,N=100) Binomial PDF(P=0.25,N=100) 02 0.1 0.15 0.075 0.1 0.05 五 005 0.25 0 20 40x60 80 100 0 20 40x60 80 100 Binomial PDF(P=0.50,N=100) Binomial PDF(P=0.75,N=100) 0.08 0.1 0.07 006 0.05 0.04 otab 005 0.03 0.02 0.25 001 04 0 204060 80100 0 20 4060 80 100 X X

3.1.3 二项分布的应用 。判断一个现象是不是二项分布 ○求概率 。在遗传学上又大量应用
3.1.3 二项分布的应用 二项分布的应用 • 判断一个现象是不是二项分布 • 求概率 • 在遗传学上又大量应用