
注意:沿等温面将无热量传递,而沿和等温面相交的任何 方向,因温度发生变化则有热量的传递。温度随距离的变化程 度以沿与等温面的垂直方向为最大。 x t x x t x ( + , ) − ( , ) 对于一维温度场,等温面x及(x+Δx)的温度分别为t(x,τ)及 t(x+Δx,τ),则两等温面之间的平均温度变化率为: x t x t x x t x gradt x = + − = → ( , ) ( , ) lim 0 温度梯度: 温度梯度是向量,其方向垂直于等温面,并以温度增加的方 向为正
注意:沿等温面将无热量传递,而沿和等温面相交的任何 方向,因温度发生变化则有热量的传递。温度随距离的变化程 度以沿与等温面的垂直方向为最大。 x t x x t x ( + , ) − ( , ) 对于一维温度场,等温面x及(x+Δx)的温度分别为t(x,τ)及 t(x+Δx,τ),则两等温面之间的平均温度变化率为: x t x t x x t x gradt x = + − = → ( , ) ( , ) lim 0 温度梯度: 温度梯度是向量,其方向垂直于等温面,并以温度增加的方 向为正

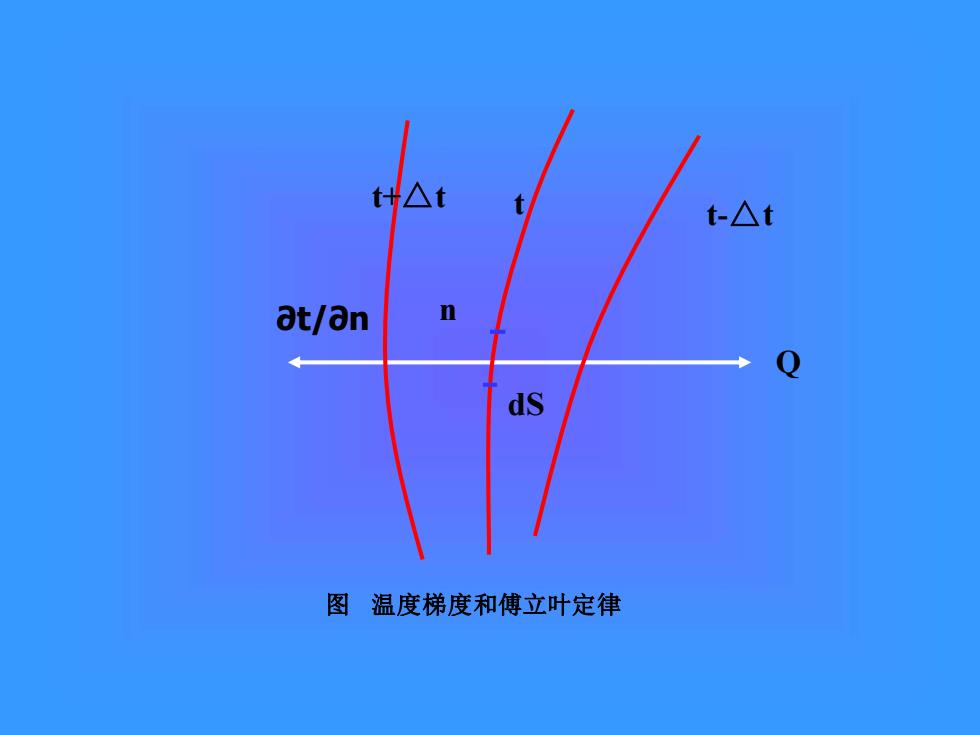
(2) 温度梯度 n t n t gradt n = = →0 lim t+t t-t t n Q dA 温度梯度是一个点的概念。 温度梯度是一个向量。 方向垂直于该点所在等温面,以温度增的方向为正 一维稳定热传导 dt / dx
(2) 温度梯度 n t n t gradt n = = →0 lim t+t t-t t n Q dA 温度梯度是一个点的概念。 温度梯度是一个向量。 方向垂直于该点所在等温面,以温度增的方向为正 一维稳定热传导 dt / dx

3.1.3 传热速率与热通量 传热速率(热流量):单位时间通过传热面积的 热量。用Q表示,单位W (J/s)。 热通量(热流密度):单位时间通过单位传热面 积的热量q ,单位W/m2 dS dQ q = 热阻(阻力) 传热温度差(推动力) 传热速率=
3.1.3 传热速率与热通量 传热速率(热流量):单位时间通过传热面积的 热量。用Q表示,单位W (J/s)。 热通量(热流密度):单位时间通过单位传热面 积的热量q ,单位W/m2 dS dQ q = 热阻(阻力) 传热温度差(推动力) 传热速率=

x t dQ dS = − 傅立叶定律是热传导的基本定律,它指出:单位时间内传导 的热量与温度梯度及垂直于热流方向的截面积成正比,即 式中 Q——单位时间传导的热量,简称传热速率,w S——导热面积,即垂直于热流方向的表面积,m2 λ——导热系数(thermal conductivity),w/m.k。 式中的负号指热流方向和温度梯度方向相反。 3.2.1傅立叶定律与热导率 x t d d q = − 3.2 热传导
x t dQ dS = − 傅立叶定律是热传导的基本定律,它指出:单位时间内传导 的热量与温度梯度及垂直于热流方向的截面积成正比,即 式中 Q——单位时间传导的热量,简称传热速率,w S——导热面积,即垂直于热流方向的表面积,m2 λ——导热系数(thermal conductivity),w/m.k。 式中的负号指热流方向和温度梯度方向相反。 3.2.1傅立叶定律与热导率 x t d d q = − 3.2 热传导
n dS Q t+△t t t-△t ∂t/∂n 图 温度梯度和傅立叶定律
n dS Q t+△t t t-△t ∂t/∂n 图 温度梯度和傅立叶定律