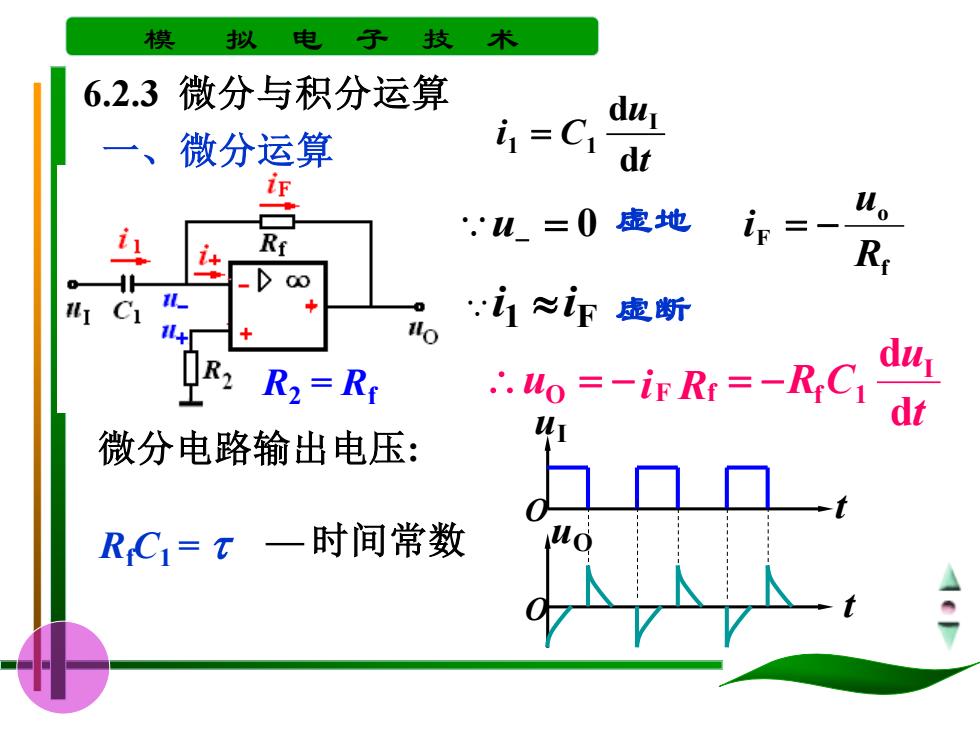
模 拟 电 子 技 术 6.2.3微分与积分运算 dur 一、微分运算 iF .W=0虚地 in= Ri 00 i心ip虚断 l+ ∴.uo=-irRr=-RCi dt 微分电路输出电压: RC1=t一时间常数
模 拟 电 子 技 术 6.2.3 微分与积分运算 t u i C d d I 1 = 1 R2 = Rf = 0 u− 虚地 f o F R u i = − 1 F i i 虚断 t u u i R R C d d I O = − F f = − f 1 RfC1 = — 时间常数 微分电路输出电压: 一、微分运算 uI O t uO O t
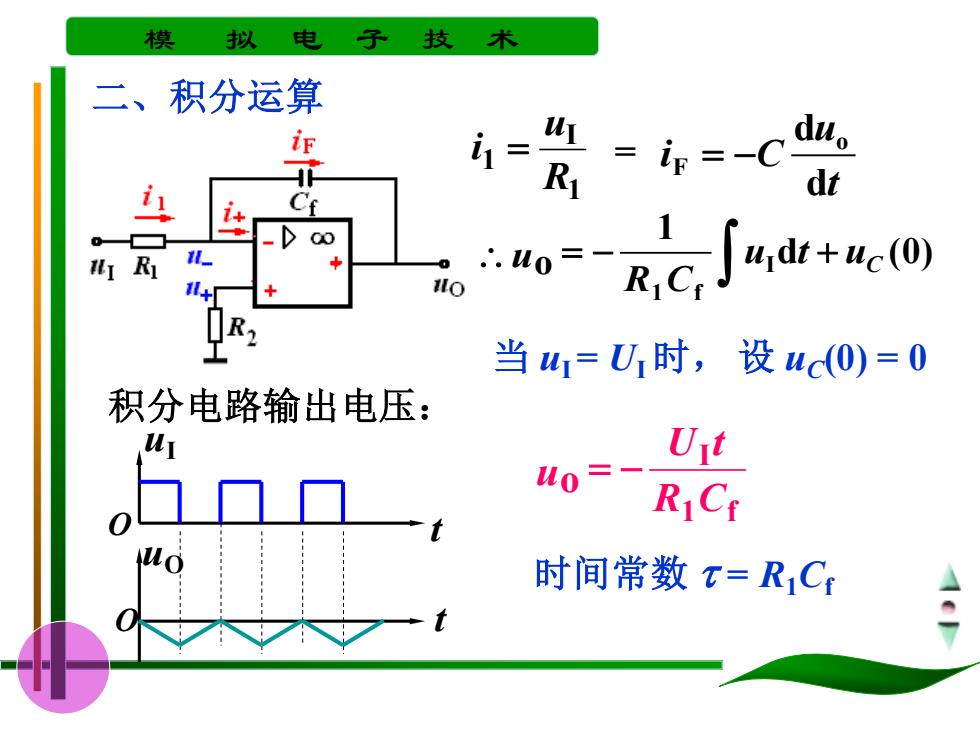
模 拟 电 子 技 二、积分运算 i1= ==-C duo dt 1 R 当u1=U时,设uc(0)=0 积分电路输出电压: 41 Ut R]Cr 时间常数T=R1Cf
模 拟 电 子 技 术 二、积分运算 1 I 1 R u i = t u i C d d o = F = − d (0) 1 o I 1 f uC u t R C u = − + 当 uI = UI 时, 1 f I o R C U t u = − 设 uC(0) = 0 时间常数 = R1Cf 积分电路输出电压: t uI O t uO O
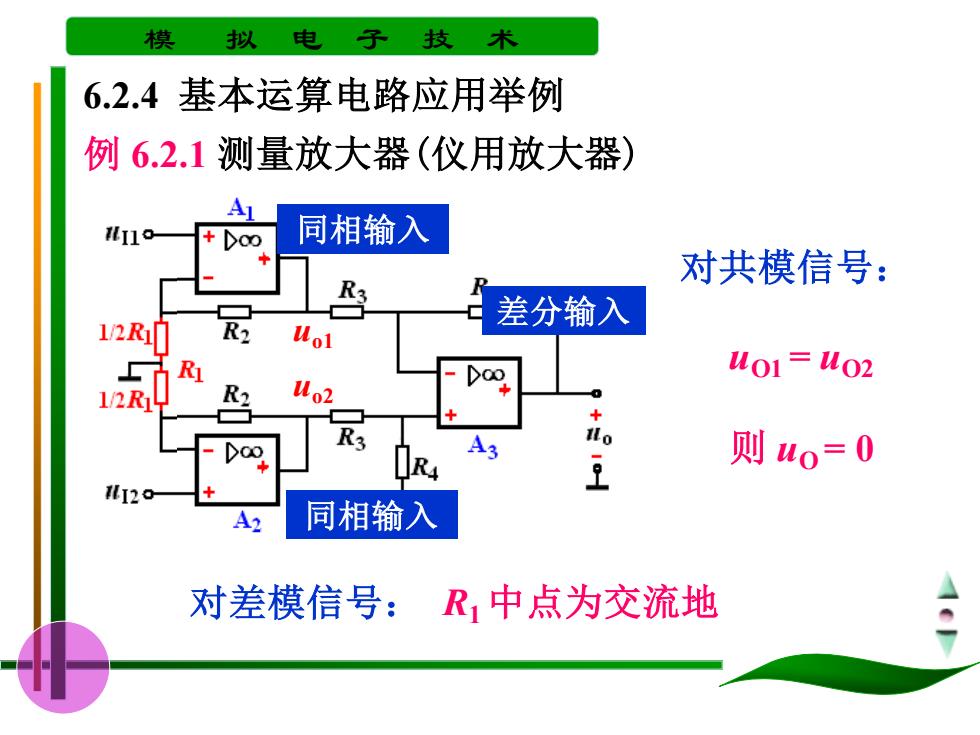
模 拟 电 子技 术 6.2.4基本运算电路应用举例 例6.2.1测量放大器(仪用放大器) 同相输入 对共模信号: 差分输入 1/2Rh R2 Mol R W01=W02 12R R2 Wo2 D00 R3 A3 豆 则uo=0 A 同相输入 对差模信号:R1中点为交流地
模 拟 电 子 技 术 6.2.4 基本运算电路应用举例 例 6.2.1 测量放大器(仪用放大器) 同相输入 同相输入 差分输入 uo1 uo2 对共模信号: uO1 = uO2 则 uO = 0 对差模信号: R1 中点为交流地
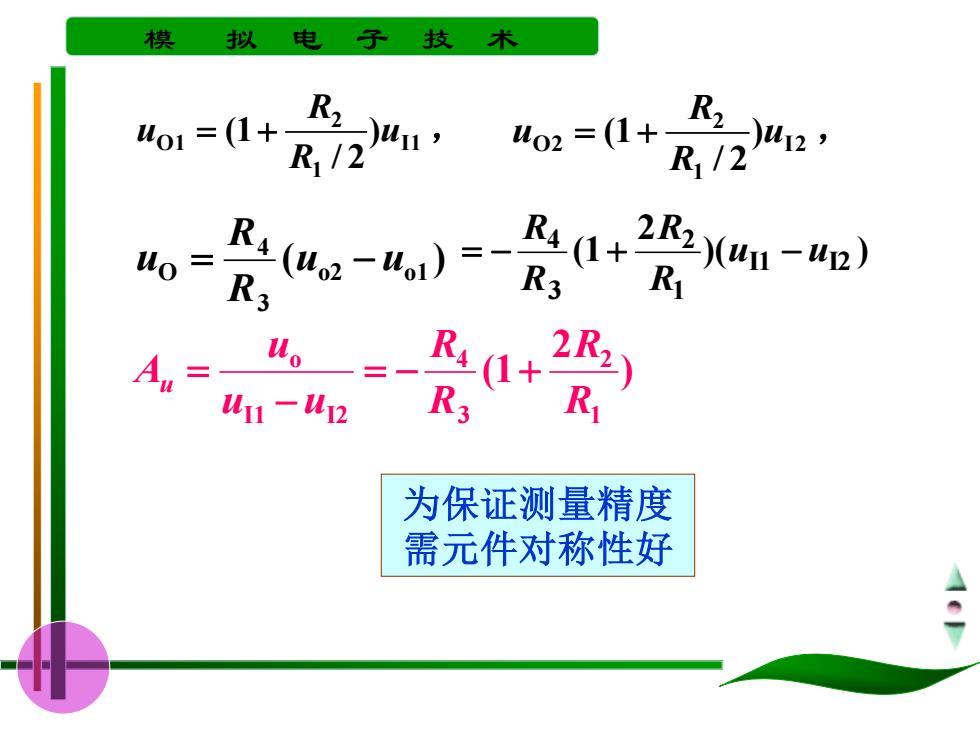
模 拟 电 子 技术 4o1=(1+R,12 o2=(1+R,/2 R4(0u-4i)= R3 R241-4) R40+R 。一= 2R2\ Au= W11-2 R3 R 为保证测量精度 需元件对称性好
模 拟 电 子 技 术 ) / 2 (1 I1 1 2 O1 u , R R u = + ) / 2 (1 I2 1 2 O2 u , R R u = + ( ) o2 o1 3 4 O u u R R u = − )( ) 2 (1 I1 I2 1 2 3 4 u u R R R R = − + − ) 2 (1 1 2 3 4 I1 I2 o R R R R u u u Au = − + − = 为保证测量精度 需元件对称性好
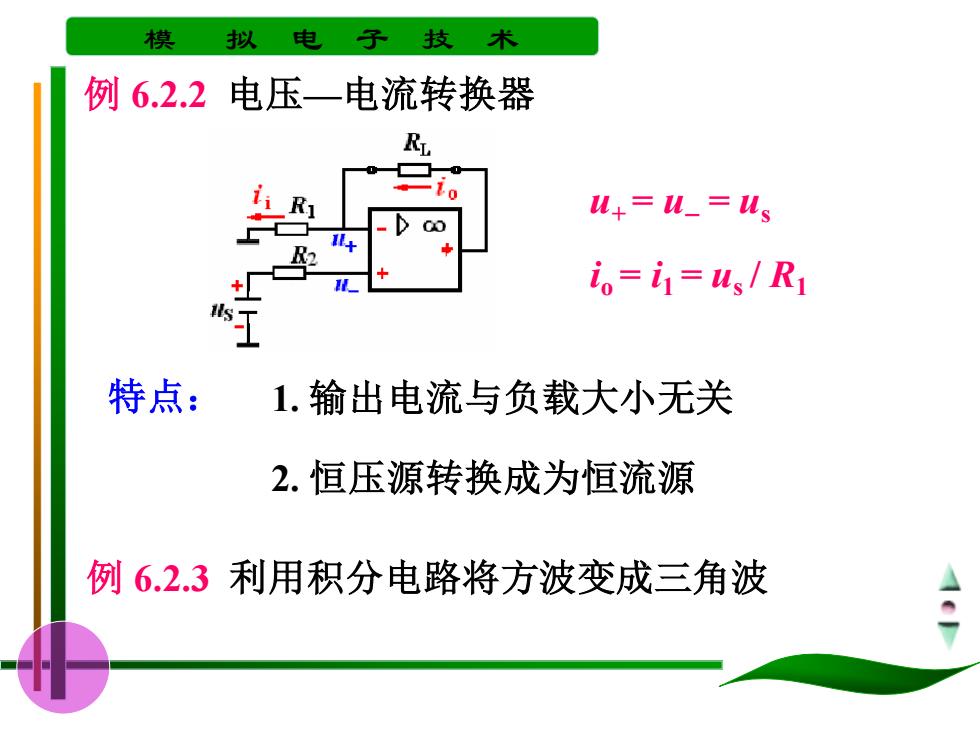
模 拟 电 子技术 例6.2.2 电压一电流转换器 R u=u_=ls 00 io=i=us/R T 特点: 1.输出电流与负载大小无关 2.恒压源转换成为恒流源 例6.2.3利用积分电路将方波变成三角波
模 拟 电 子 技 术 u+ = u− = us io = i1 = us / R1 1. 输出电流与负载大小无关 2. 恒压源转换成为恒流源 特点: 例 6.2.2 电压—电流转换器 例 6.2.3 利用积分电路将方波变成三角波