若G是网络,则邻接矩阵可定义为: A[i,j]= t [例3]带权图的邻接矩阵 0123 3 0 0358 1 30004 5 8 4 2 50002 3 8420 N2 2
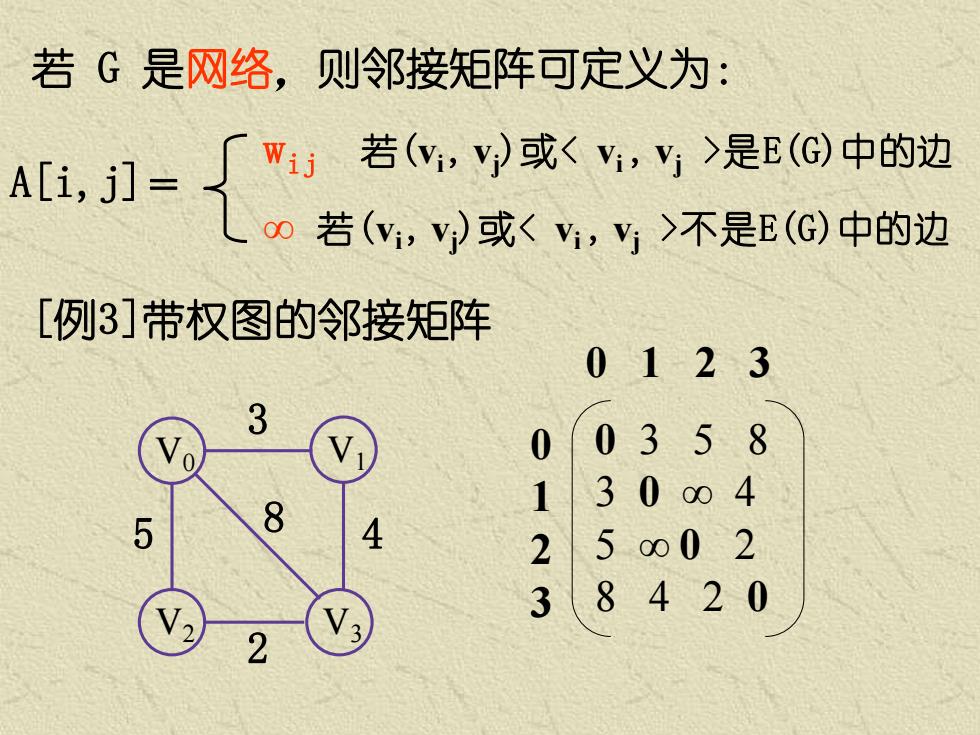
若 G 是网络,则邻接矩阵可定义为: [例3]带权图的邻接矩阵 0 1 2 3 0 3 5 8 3 0 ∞ 4 5 ∞ 0 2 8 4 2 0 0 1 2 3 V0 V2 V3 V1 3 5 2 8 4 A[i,j]= wij 若(vi , vj)或< vi , vj >是E(G)中的边 ∞ 若(vi , vj)或< vi , vj >不是E(G)中的边
7.2.2邻接表 。定义:由顺序存储的顶点表和链接存储的边链表 构成的图的存储结构被称为邻接表。 [例1]无向图的邻接表。 0 123Λ 0 3Λ 2 3Λ 2 3 3 12Λ
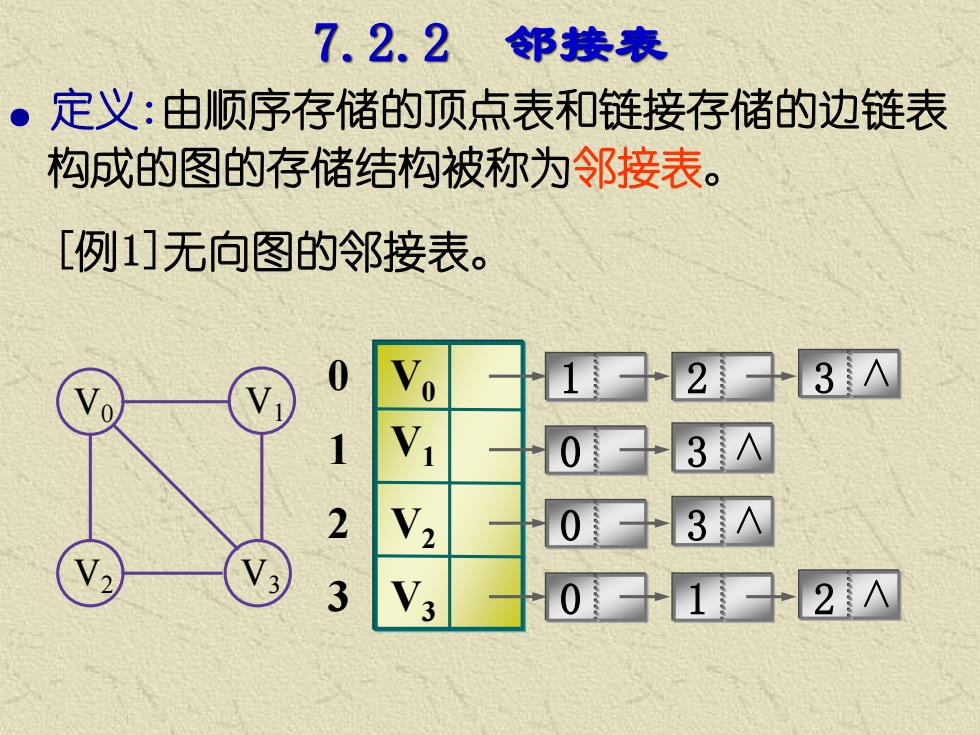
7.2.2 邻接表 ● 定义:由顺序存储的顶点表和链接存储的边链表 构成的图的存储结构被称为邻接表。 [例1]无向图的邻接表。 V0 V2 V3 V1 V0 V1 V2 V3 0 2 3 1 1 2 3 ∧ 0 1 2 ∧ 0 3 ∧ 0 3 ∧
[例2]有向图的邻接表。 0 1 1 03 4Λ 2 3∧ 3 4 3Λ
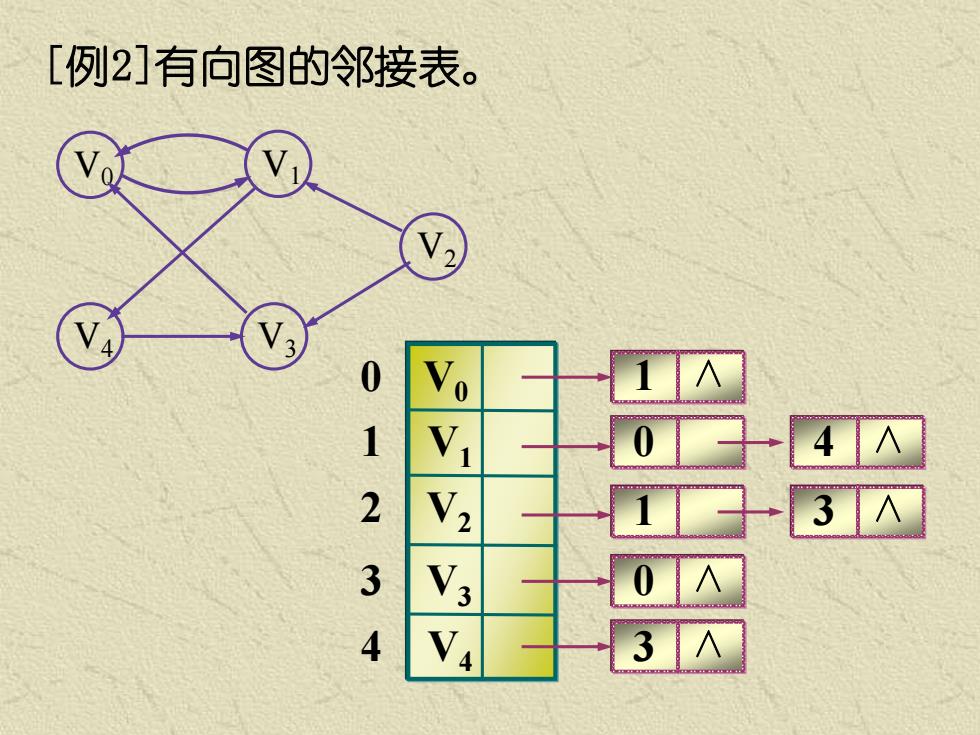
[例2]有向图的邻接表。 V0 V1 V2 V3 V4 0 2 4 3 1 1 ∧ 3 ∧ 0 ∧ 0 ∧ 4 ∧ 1 ∧ 3 ∧ V0 V4 V3 V1 V2
[例3]有向图的逆邻接表。 3 0 13∧ 1 02 2 V2 3 24 3 4 4 1
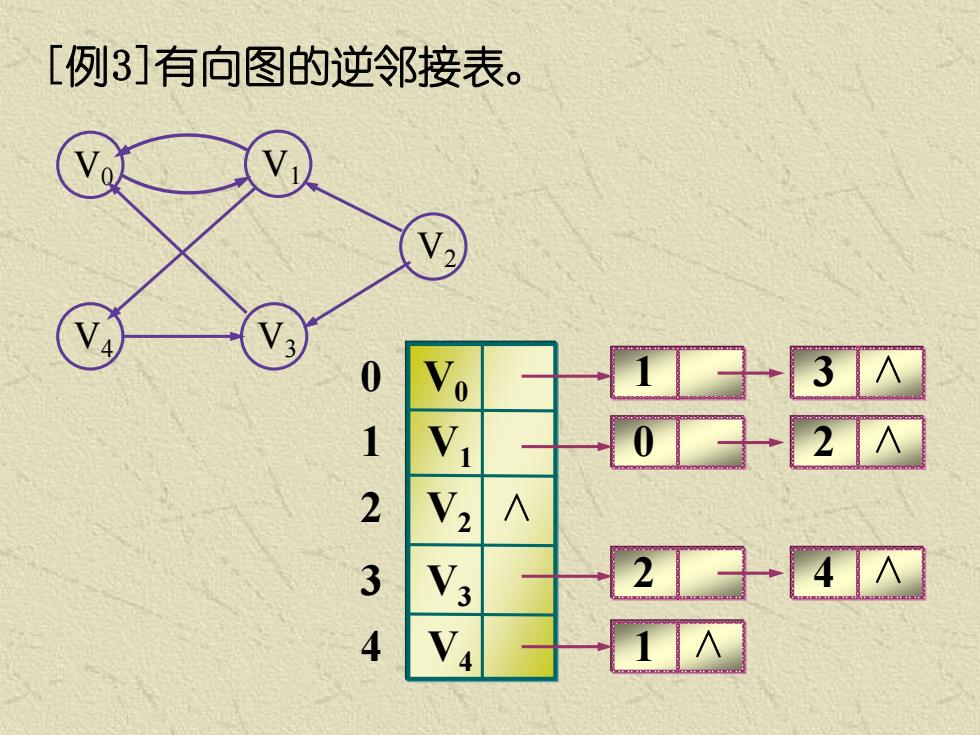
[例3]有向图的逆邻接表。 V0 V4 V3 V1 V2 V0 V1 V2 V3 V4 0 2 4 3 1 1 ∧ 0 ∧ 2 ∧ 2 ∧ 4 ∧ 1 ∧ 3 ∧ ∧
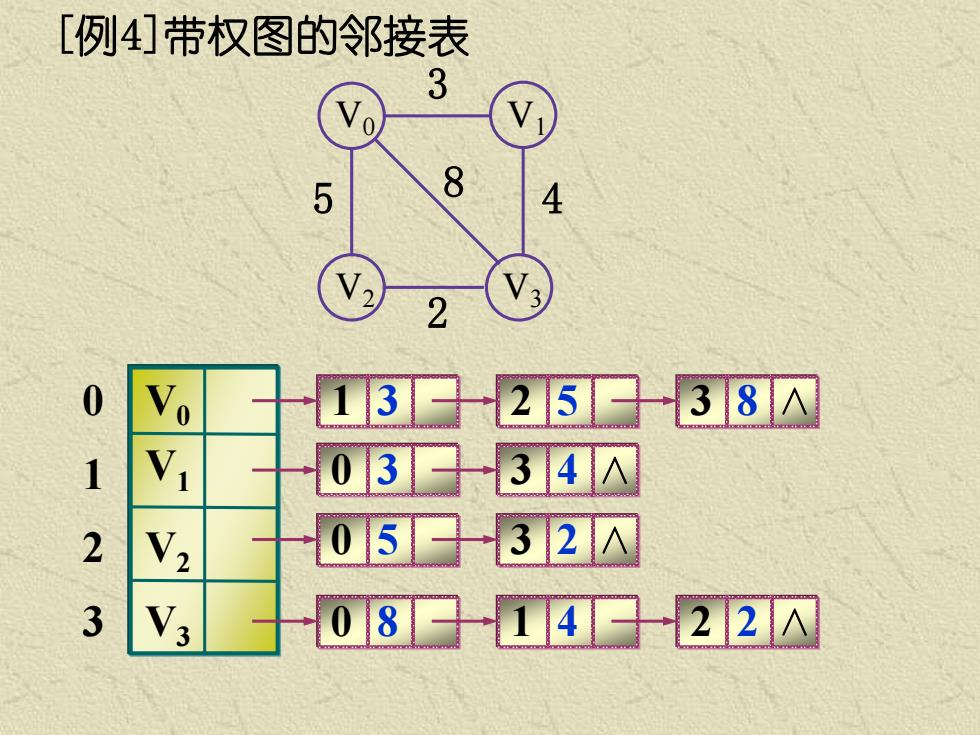
[例4]带权图的邻接表 3 0 5 8 4 2 0 13□25E38N 1 0334 2 0532△ 3 081422N
[例4]带权图的邻接表 V0 V2 V3 V1 3 5 2 8 4 V0 V1 V2 V3 0 2 3 1 1 3 2 5 3 8 ∧ 0 8 1 4 2 2 ∧ 0 5 3 2 ∧ 0 3 3 4 ∧