
⑥可及和连通分量: 若从顶点v到顶点v有路径,则称v与V可及(连 通的)。 ◆ 若G为无向图,且V(G)中任意两顶点都可及, 则称G为连通图。 无向图G的极大连通子图称为G的连通分量。 ⑦强连通图和强连通分量: 若G为有向图,且对于V(G)中任意两个不同的 顶点v和y,v与y可及,V与v也可及,则称 G为强连通图。 有向图G的极大强连通子图称为G的强连通分量
⑥ 可及和连通分量 : 若从顶点vi到顶点vj有路径,则称vi与vj可及(连 通的)。 若G为无向图,且V(G)中任意两顶点都可及, 则称G为连通图。 无向图G的极大连通子图称为G的连通分量。 ⑦ 强连通图和强连通分量 : 若G为有向图,且对于V(G)中任意两个不同的 顶点vi和vj , vi与vj可及, vj与vi也可及,则称 G为强连通图。 有向图G的极大强连通子图称为G的强连通分量

⑧权和网: ·在一个图中,每条边可以标上具有某种含义的 数值,此数值称为该边的权。 边上带有权的图称做带权图(网)
⑧ 权和网: 在一个图中,每条边可以标上具有某种含义的 数值,此数值称为该边的权。 边上带有权的图称做带权图(网)

7.2图的存储结构 7.2.1邻接矩阵 。定义:表示顶点之间相邻关系的矩阵叫邻接矩阵。 具有n个顶点的图G(W,E)是具有下列性质的n阶 方阵: to Ai,]= 若(,)或<V,y>是E(G)中的边 若(v,)或<V,y>不是E(G)中的边
7.2 图的存储结构 7.2.1 邻接矩阵 ● 定义:表示顶点之间相邻关系的矩阵叫邻接矩阵。 具有n个顶点的图G=(V,E)是具有下列性质的n阶 方阵: A[i,j]= 1 若(vi , vj)或< vi , vj >是E(G)中的边 0 若(vi , vj)或< vi , vj >不是E(G)中的边
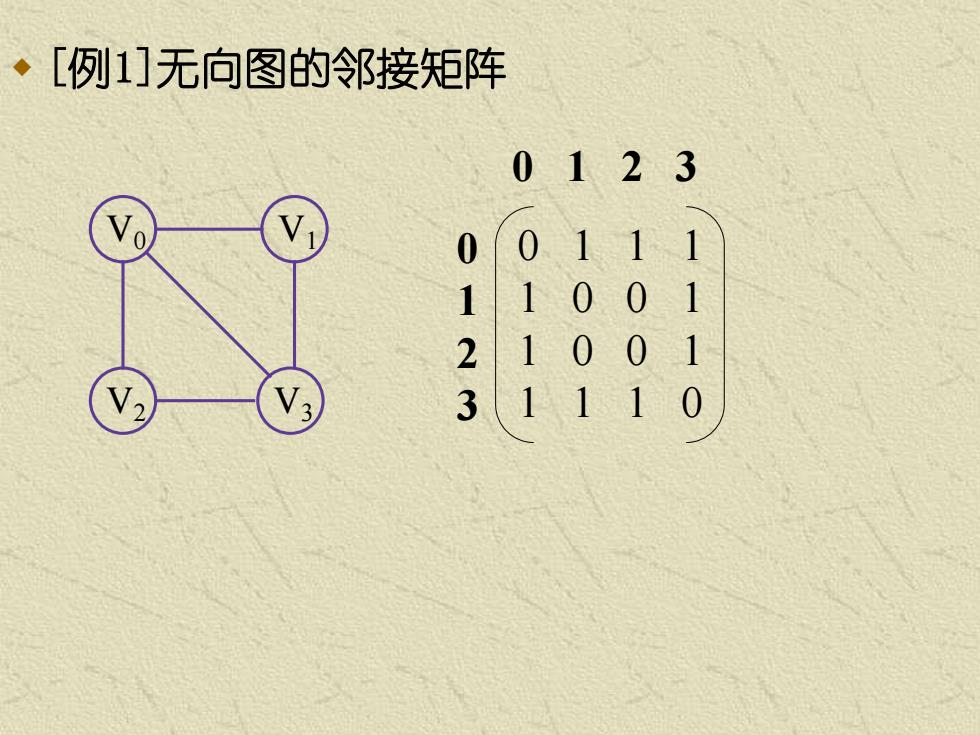
·[例1]无向图的邻接矩阵 0123 0 0111 1 1001 2 100 1 3 111
[例1]无向图的邻接矩阵 0 1 2 3 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 0 0 1 2 3 V0 V2 V3 V1
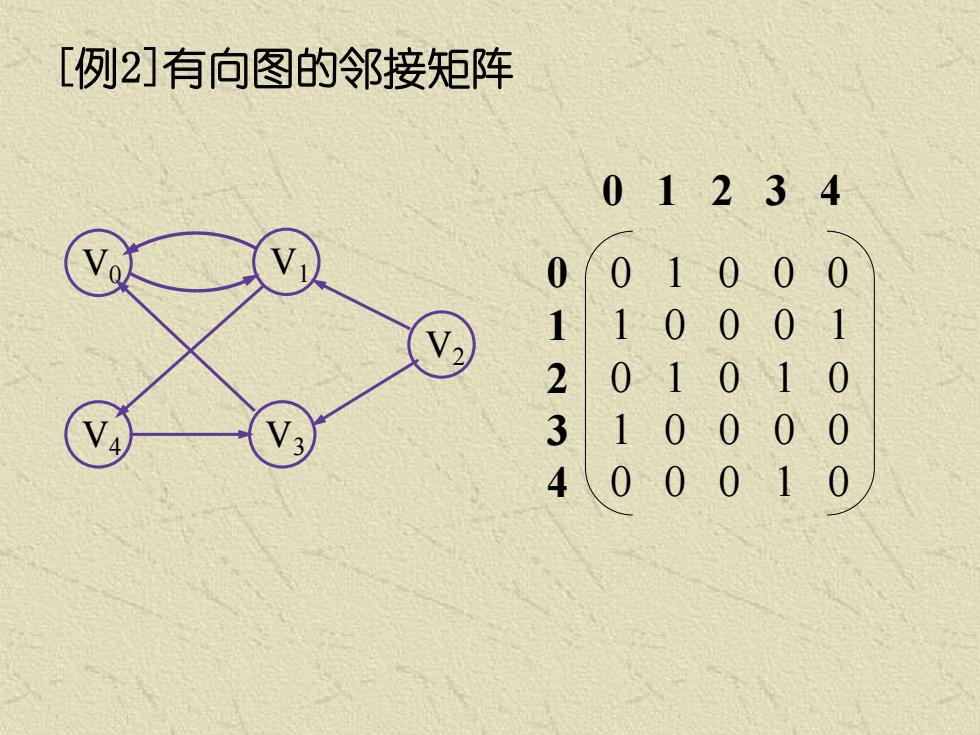
[例2]有向图的邻接矩阵 0123.4 001000 1 10001 2 2 01010 3 3 10000 4 00010
[例2]有向图的邻接矩阵 V0 V4 V3 V1 V2 0 1 2 3 4 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 1 2 3 4