
KYLE INFORMED SPECULATION 327 (30)and the residual supply schedule (21),together with(22)and (23),to write the optimal x and resulting p*as 请=k立+(k,-1in+k (31) 2入,+p1/r* [A(1+k)+pi/"m+ki.+k (32) 2入+P1/x* Case 1A.For case 1A,the coefficient of pin in (32)is non-zero.Thus,(32)can be solved for pim in terms of p*and in.Plugging the result into (31)to express x as a function of in and p*rather than in and pim yields x特=k+k,-1)p*+k3 入(1+k)+p/r* if入(1+k1)+P/x*≠0. (33) Alternatively,observe that since the coefficient of pin in(32)is non-zero,linear combina- tions of p*and in span the same space as linear combinations of pim and in.Thus, E{pm,in)=E{p*,in).Using this fact and the residual supply schedulep*= pm+入,x*,(30)can be rewritten 漆E{创户,动-方萨+Ax选 (34) 2A,+p/r* Solving for x*in terms of p*and in yields 特-E⊙创选,-户 (35) 入,+P1/r* This is equivalent to(33). Case 1B.For Case 1B,the coefficient of pim in(32)is zero,the demand curve is a correspondence with the same price for each quantity,and(32)becomes p*-.+) ifA(1+k)+p/r*=0. (36) 2入1+pP1/r* This is the only case where the special assumptions underlying the market clearing rules come into play,and it does not arise in the equilibrium discussed below. Lemma 5.1 says that a monopolist has a demand schedule.That a monopsonist has a demand curve is at first glance a surprising proposition,since textbooks tell us otherwise. Figure 1 illustrates graphically the intuition behind the result.In the figure,MV denotes the monopsonist's marginal valuation schedule(the left-hand side of(29)),S denotes the supply schedule,and MS denotes the corresponding marginal cost schedule (the right-hand side of(29)).Equating marginal cost to marginal value yields the price-quantity pair chosen by the monopsonist.Now if the supply curve S shifts outward to S,this makes the marginal valuation schedule MV shift outward(to MV)as well,because the informed speculator's observation of his supply schedule affects his valuation.The new price-quantity combination is denoted x,p*.An analogous effect occurs if the supply schedule shifts downward to S".Now observe that the graph of maximizing price-quantity pairs for all supply schedules is the heavy-shaded straight line D.This line is the monopsonist's demand schedule
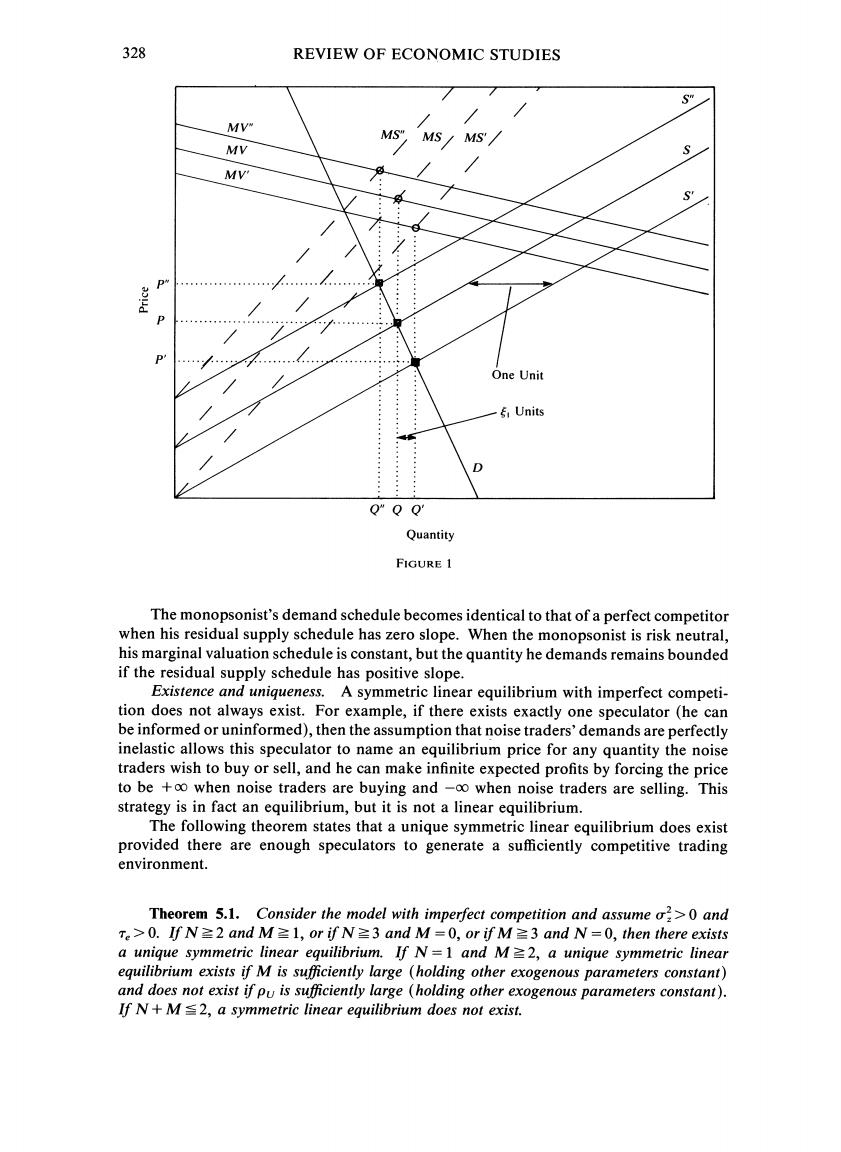
328 REVIEW OF ECONOMIC STUDIES Sm MV MS" MS MS' MV MV' One Unit 6 Units 0 Q"Q Q' Quantity FIGURE 1 The monopsonist's demand schedule becomes identical to that of a perfect competitor when his residual supply schedule has zero slope.When the monopsonist is risk neutral, his marginal valuation schedule is constant,but the quantity he demands remains bounded if the residual supply schedule has positive slope. Existence and uniqueness.A symmetric linear equilibrium with imperfect competi- tion does not always exist.For example,if there exists exactly one speculator (he can be informed or uninformed),then the assumption that noise traders'demands are perfectly inelastic allows this speculator to name an equilibrium price for any quantity the noise traders wish to buy or sell,and he can make infinite expected profits by forcing the price to be +oo when noise traders are buying and -oo when noise traders are selling.This strategy is in fact an equilibrium,but it is not a linear equilibrium. The following theorem states that a unique symmetric linear equilibrium does exist provided there are enough speculators to generate a sufficiently competitive trading environment. Theorem 5.1.Consider the model with imperfect competition and assume o2>0 and Te>0.IfN≥2andM≥l,or ifN≥3andM=0,or ifM≥3andN=0,then there exists a unique symmetric linear equilibrium.If N=1 and M=2,a unique symmetric linear equilibrium exists if M is sufficiently large (holding other exogenous parameters constant) and does not exist if pu is sufficiently large (holding other exogenous parameters constant). If N+M2,a symmetric linear equilibrium does not exist

KYLE INFORMED SPECULATION 329 Comments.A linear equilibrium does not always exist because,with infinitely inelastic demand by noise traders,speculators may have "too much"monopoly of power if there are not enough of them.We suspect(but do not prove in this paper)that with elastic noise trader demand (of the form 2-sp,s>0,s small),a unique symmetric linear equilibrium does exist.Note that with Cournot oligopoly,nonexistence is an even greater problem,since equilibrium never exists when demand is infinitely inelastic. In the existence part of the result,the strategy functions are not merely "best linear. strategies".Instead,the linearity of the strategies is a derived result in the sense that for each speculator,the equilibrium linear strategy dominates all non-linear alternatives.In the uniqueness part of the result,linearity is a constraint.This paper does not investigate whether equilibria with non-linear strategy functions exist.In the uniqueness part of the theorem,symmetry is also a constraint.We conjecture that the theorem could be general- ized to remove this constraint by constructing a proof which allows traders to conjecture linear strategy functions which differ from trader to trader,then prove that they are all the same in equilibrium,but this is not attempted here.Finally,the theorem can easily be generalized to state that it is not optimal for traders to randomize trading strategies. This result,like linearity,follows from the Nash equilibrium framework,which makes each speculator's profit objective equivalent to a quadratic one.Both results might disappear if some other equilibrium concept is used. Proof.Here the basic ideas involved in the proof of Theorem 5.1 are discussed. This discussion considers only the case where there are at least two informed speculators and one uninformed speculator,i.e.N=2 and M=1.Part of this proof and proofs for other cases are contained in Appendix B. The approach of this proof is to derive necessary conditions for an equilibrium,then show that they are sufficient. In a symmetric linear equilibrium with imperfect competition,all of the notation and results from Section 4 concerning measures of informational efficiency are applicable. Accordingly,postulate an imperfectly competitive equilibrium with strategy functions (for n=1,...,N and m=1,...,M) Xn(p,in)=uI+Bin-Yip,Ym(p)=uu-Yup (37) It can be inferred from the market-clearing condition, ∑N1Xn(iia)+∑M1Ym()+=0, (38) that the equilibrium price is given by 币=(B∑N,n+三+Na,+Muu), (39) where the slope of the market supply curve A(calculated as a function of the quantity traded by noise traders z)is given by A=(Nyi+Myu)1. (40) Here,it is a necessary condition for equilibrium that the quantity A be well-defined(i.e. Nyr+Myu0)because otherwise the market-clearing rules imply the price is infinite, in which case X and Yn are not optimal and therefore do not sustain an equilibrium as postulated. In addition,the market-clearing condition makes it possible to define a residual supply curve for each speculator.Denoting slopes A,and Au by ,=[(N-1)M+Myu],Au=[N+(M-1)Yu], (41)