
第11卷第2期 智能系统学报 Vol.11No.2 2016年4月 CAAI Transactions on Intelligent Systems Apr.2016 D0I:10.11992/is.201509017 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160314.1431.004.html 多小波和NSDFB组合域递归滤波多聚焦图像融合 任晓霞,孙秀明,耿鹏2,苏醒2 (1.张家口学院理学系,河北张家口075000:2.石家庄铁道大学信息科学与技术学院,河北石家庄050043) 摘要:多小波能同时满足正交、紧支、对称等对信号处理十分重要的特性,结合多小波变换的多尺度特点和非子采 样方向滤波器组变换的多方向性,提出了一种新的基于多小波和非子采样方向滤波器组的多尺度多方向变换。对 于高频系数首先计算其修改空间频率,然后利用域变换递归滤波进行滤波的融合规则:低频系数采用了修改拉普拉 斯能量和的(SML)融合规则。通过与其他融合方法进行实验对比,实验结果表明:本文提出的融合方法能够更加有 效地选择源图像中的聚焦良好区域,并且引入的伪影信息较少:此外,与其他融合方法相比本文方法的客观评价结 果也是最好的。 关键词:图像处理;图像融合:递归滤波;改进空间频率:多小波 中图分类号:TP391文献标志码:A文章编号:1673-4785(2016)02-0241-08 中文引用格式:任晓霞,孙秀明,耿鹏,等.多小波和NSDFB组合域递归滤波多聚焦图像融合[J].智能系统学报,2016,11(2): 241-248. 英文引用格式:REN Xiaoxia,SUN Xiuming,GENG Peng,etal.Multifocus image fusion using a recursive filter in the combined domain of multiwavelets and NSDFB[].CAAI transactions on intelligent systems,2016,11(2):241-248. Multifocus image fusion using a recursive filter in the combined domain of multiwavelets and NSDFB REN Xiaoxia',SUN Xiuming',GENG Peng2,SU Xing? (1.Science department,Zhangjiakou University,Zhangjiakou 075000,China;2.School of Information Science and Technology,Shi- jiazhuang Tiedao University,Shijiazhuang 050043,China) Abstract:The multiwavelet transform has properties of orthogonality,tight frame,and symmetry,which are vital to signal processing.In this study,a new transform,called as MNSDFB,is proposed by combining the multi-wavelet and nonsubsampled directional filter banks.The domain transform recursive filter is adopted to fuse the filters after the spatial frequency of the high frequency coefficient is calculated.The modified sum-modified-Laplacian (SML) is employed in the low pass subbands as a focus measurement to select fused coefficients.The presented fusion rule in the high pass subband can distinguish the focused regions from the blurred regions.The proposed fusion method was compared with three other fusion methods.The experimental results demonstrate that the proposed fusion meth- od can select the focused regions while introducing few artifacts into the final merged image.Furthermore,its objec- tive criteria,such as MI and QAB/F,are better than those of the other three methods. Keywords:image processing;image fusion;recursive filter;modified spatial frequency;multiwavelett 图像融合是信息融合的一个重要分支,其目的 一幅新的具有更高可信度清晰度以及可理解性的图 是将不同传感器获取的同一目标的互补信息合并为 像[山。因此,经过图像融合技术得到的合成图像可 以更全面、更精确地描述所研究的对象,为进一步图 收稿日期:2015-09-09.网络出版日期:2016-03-14. 像处理和分析提供高质量数据。因此,图像融合技 基金项目:河北省自然科学基金项目(F2013210094,F2013210109). 通信作者:耿鹏.E-mail:Gengpeng(@stdu.cdu.cn. 术在军事、医学、遥感、计算机视觉等领域得到了广
第 11 卷第 2 期 智 能 系 统 学 报 Vol.11№.2 2016 年 4 月 CAAI Transactions on Intelligent Systems Apr. 2016 DOI:10.11992 / tis.201509017 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160314.1431.004.html 多小波和 NSDFB 组合域递归滤波多聚焦图像融合 任晓霞1 ,孙秀明1 ,耿鹏2 ,苏醒2 (1.张家口学院 理学系, 河北 张家口 075000; 2.石家庄铁道大学 信息科学与技术学院, 河北 石家庄 050043) 摘 要:多小波能同时满足正交、紧支、对称等对信号处理十分重要的特性,结合多小波变换的多尺度特点和非子采 样方向滤波器组变换的多方向性,提出了一种新的基于多小波和非子采样方向滤波器组的多尺度多方向变换。 对 于高频系数首先计算其修改空间频率,然后利用域变换递归滤波进行滤波的融合规则;低频系数采用了修改拉普拉 斯能量和的(SML)融合规则。 通过与其他融合方法进行实验对比,实验结果表明:本文提出的融合方法能够更加有 效地选择源图像中的聚焦良好区域,并且引入的伪影信息较少;此外,与其他融合方法相比本文方法的客观评价结 果也是最好的。 关键词:图像处理;图像融合;递归滤波;改进空间频率;多小波 中图分类号: TP391 文献标志码:A 文章编号:1673⁃4785(2016)02⁃0241⁃08 中文引用格式:任晓霞,孙秀明,耿鹏,等. 多小波和 NSDFB 组合域递归滤波多聚焦图像融合[ J]. 智能系统学报, 2016, 11( 2): 241⁃248. 英文引用格式:REN Xiaoxia, SUN Xiuming, GENG Peng, et al. Multifocus image fusion using a recursive filter in the combined domain of multiwavelets and NSDFB[J]. CAAI transactions on intelligent systems, 2016, 11(2): 241⁃248. Multifocus image fusion using a recursive filter in the combined domain of multiwavelets and NSDFB REN Xiaoxia 1 , SUN Xiuming 1 , GENG Peng 2 , SU Xing 2 (1. Science department , Zhangjiakou University, Zhangjiakou 075000, China; 2. School of Information Science and Technology, Shi⁃ jiazhuang Tiedao University, Shijiazhuang 050043, China) Abstract:The multiwavelet transform has properties of orthogonality, tight frame, and symmetry, which are vital to signal processing. In this study, a new transform, called as MNSDFB, is proposed by combining the multi⁃wavelet and nonsubsampled directional filter banks. The domain transform recursive filter is adopted to fuse the filters after the spatial frequency of the high frequency coefficient is calculated. The modified sum⁃modified⁃Laplacian (SML) is employed in the low pass subbands as a focus measurement to select fused coefficients. The presented fusion rule in the high pass subband can distinguish the focused regions from the blurred regions. The proposed fusion method was compared with three other fusion methods. The experimental results demonstrate that the proposed fusion meth⁃ od can select the focused regions while introducing few artifacts into the final merged image. Furthermore, its objec⁃ tive criteria, such as MI and QAB / F, are better than those of the other three methods. Keywords: image processing; image fusion; recursive filter; modified spatial frequency; multiwavelett 收稿日期:2015⁃09⁃09. 网络出版日期:2016⁃03⁃14. 基金项目:河北省自然科学基金项目(F2013210094, F2013210109). 通信作者:耿鹏.E⁃mail:Gengpeng@ stdu.edu.cn. 图像融合是信息融合的一个重要分支,其目的 是将不同传感器获取的同一目标的互补信息合并为 一幅新的具有更高可信度清晰度以及可理解性的图 像[1] 。 因此,经过图像融合技术得到的合成图像可 以更全面、更精确地描述所研究的对象,为进一步图 像处理和分析提供高质量数据。 因此,图像融合技 术在军事、医学、遥感、计算机视觉等领域得到了广

.242. 智能系统学报 第11卷 泛的应用)。一般来说,图像融合方法可以分为两 通过等距变换映射到五维空间中,并保持曲线上 类:空域融合方法和变换域融合方法。空域方法根 每个点之间的距离不变,通过自适应地改变输入 据图像的清晰判别准则选择源图像中的像素,从而 信号,将滤波运算降到了一维上,使得域变换滤 形成一幅融合后的图像。空域方法一般有空间频率 波计算复杂度不受相关参数影响,因此,DTRF在 (SF)、拉普拉斯能量(EOL)、修改拉普拉斯能量和 保持图像边缘的同时,具有实时性的优点。本文 (SML)等方法[)。根据采用不同的变换,变换域方 在提出的MNSDFB变换基础上,提出了结合修改 法可以分为小波变换、Contourlet变换、非子采样 空间频率的域变换递归滤波的多聚焦图像融合 Contourlet变换以及Shearlet变换[a等方法。 方法。 苗启广[)提出了一种小波域基于区域局部能量 1 域变换递归滤波 的不同聚焦点图像融合方法,取得了很好的融合效 果。传统的小波变换虽能高效处理和分析一维分段 Gastal!山在域变换基础上提出了边缘保持平滑 连续信号,但由一维小波通过张量积而形成的二维小 递归滤波器(DTRF),它的基本思路可以理解为先 波基不满足各向异性的尺度关系,小波变换无法精确 降低输入信号的维数再进行低维滤波。在五维空间 地表述图像边缘信息,基于小波变换融合的图像容易 中,一个边缘保持的平滑滤波可以定义成一个空间 产生细节成分模糊现象[6)。多小波能同时满足正交、 不变的核H,它的响应会随着像素点间距离的变化 紧支、对称等对信号处理十分重要的特性,被广泛应 而变化,如果在某个低维空间中这些距离保持不变 用于图像融合领域[)]。王迎春)在多小波变换域对 那么核的响应也将保持不变,因而,达到了保留图像 低频和高频小波系数采用不同的融合方法,对低频系 边缘的目的)。DTRF首先将输入信号I变换到变 数采用取平均的方法,而对高频系数采用边缘梯度对 换域2.,,随后,变换域信号由递归滤波器(recursive 比的方法。该方法能够很好保存图像的边缘和细节 filter,RF)进行处理如下: 信息。但多小波是对传统的小波的扩展,仍不能解决 J[m]=(1-a)1[m]+aJ[m-1](1) 类似于小波变换无法精确地表述图像边缘方向信息 式中:J[m]是滤波后的结果,反馈系数a= 的问题。Cunhat9提出的非子采样Contourlet变换 exp(-√2/8,)∈[0,1],δ是空间参数; (nonsubsampled contourlet transform,NSCT),由于同 I[m]=[xm]为输入的离散信号。b是变换域 时具有灵活的多分辨率和多方向性表示的优点,相对 2w相邻采样点xm和xm-1之间的距离,可以由 小波变换来说,能够更好地表示图像的边缘信息。米 b=ct(xm)一ct(xm-1)计算得到。对于变换域信 德伶[1O对NSCT分解后的低频子带和高频方向子带 号I(x),ct(u)可以由式(2)得到 分别以邻域梯度及合成邻域模值作为清晰度指标,采 (2) 用自适应选择法实现对多聚焦图像的融合处理。然 c()=小1+分lr(x)lk,ueD 0 而,NSCT变换中的大量的冗余使得这些融合方法具 式中:I'(x)是I(x)的导数,6和分别是DTRF的 有较高的时间复杂度。为了同时兼顾较小的分解冗 空间参数和范围参数。由式(2)可知:随着b的增 余和分辨率多方向的优点,本文充分利用NSCT中非 大,a°趋近于零,这逐渐使得式(2)的递归过程收 子采样方向滤波器组(nonsubsampled direction filter 敛,使得滤波后输出结果中同一侧图像边缘的像素 bank,NSDFB)能够更好捕捉图像的边缘的优点和 会取得相近的值,不同侧图像边缘的像素会有很大 Multiwavelet能同时满足正交、紧支、对称的特点,将 差别,从而图像的边缘可以更好地保留下来。 Multiwavelet和NSDFB结合构建MNSDFB(multiwave- let nonsubsampled direction filter bank)变换,并利用该 2融合方法 变换进行图像融合。 2.1组合多小波与NSDFB变换 除了变换方法外,融合规则对融合的效果也 非子采样Contourlet变换中首先对图像进行非 会产生重要影响。近年来,许多学者提出了各种 子采样塔式分解,然后进行非子采样方向分解(NS 边缘保持滤波方法:双边滤波、引导滤波、域变换 DFB),从而建立了图像的多尺度、多方向的表示。 滤波、Cost-volume filtering!]等,这些边缘保持滤 根据NSCT的想法,本文利用多小波将图像分解为 波能够很好地保持图像的边缘结构。其中 一个低频系数和3个高频系数,然后利用NSDFB将 Gastal]等提出的域变换递归滤波(domain trans- 4个高频系数进行NSDFB方向分解。低频系数可 form recursive filter,DTRF)将图像中的二维曲线 以再次进行多小波分解,并再次对产生的高频系数
泛的应用[2] 。 一般来说,图像融合方法可以分为两 类:空域融合方法和变换域融合方法。 空域方法根 据图像的清晰判别准则选择源图像中的像素,从而 形成一幅融合后的图像。 空域方法一般有空间频率 (SF)、拉普拉斯能量(EOL)、修改拉普拉斯能量和 (SML)等方法[3] 。 根据采用不同的变换,变换域方 法可以分为小波变换、Contourlet 变换、非子采样 Contourlet 变换以及 Shearlet 变换[4]等方法。 苗启广[5]提出了一种小波域基于区域局部能量 的不同聚焦点图像融合方法,取得了很好的融合效 果。 传统的小波变换虽能高效处理和分析一维分段 连续信号,但由一维小波通过张量积而形成的二维小 波基不满足各向异性的尺度关系,小波变换无法精确 地表述图像边缘信息,基于小波变换融合的图像容易 产生细节成分模糊现象[6] 。 多小波能同时满足正交、 紧支、对称等对信号处理十分重要的特性,被广泛应 用于图像融合领域[7] 。 王迎春[8] 在多小波变换域对 低频和高频小波系数采用不同的融合方法,对低频系 数采用取平均的方法,而对高频系数采用边缘梯度对 比的方法。 该方法能够很好保存图像的边缘和细节 信息。 但多小波是对传统的小波的扩展,仍不能解决 类似于小波变换无法精确地表述图像边缘方向信息 的问题。 Cunha [9] 提出的非子采样 Contourlet 变换 (nonsubsampled contourlet transform, NSCT),由于同 时具有灵活的多分辨率和多方向性表示的优点,相对 小波变换来说,能够更好地表示图像的边缘信息。 米 德伶[10]对 NSCT 分解后的低频子带和高频方向子带 分别以邻域梯度及合成邻域模值作为清晰度指标,采 用自适应选择法实现对多聚焦图像的融合处理。 然 而,NSCT 变换中的大量的冗余使得这些融合方法具 有较高的时间复杂度。 为了同时兼顾较小的分解冗 余和分辨率多方向的优点,本文充分利用 NSCT 中非 子采样方向滤波器组(nonsubsampled direction filter bank, NSDFB)能够更好捕捉图像的边缘的优点和 Multiwavelet 能同时满足正交、紧支、对称的特点,将 Multiwavelet 和 NSDFB 结合构建 MNSDFB(multiwave⁃ let nonsubsampled direction filter bank)变换,并利用该 变换进行图像融合。 除了变换方法外,融合规则对融合的效果也 会产生重要影响。 近年来,许多学者提出了各种 边缘保持滤波方法:双边滤波、引导滤波、域变换 滤波、Cost⁃volume filtering [ 11] 等,这些边缘保持滤 波 能 够 很 好 地 保 持 图 像 的 边 缘 结 构。 其 中 Gastal [ 11]等提出的域变换递归滤波( domain trans⁃ form recursive filter, DTRF) 将图像中的二维曲线 通过等距变换映射到五维空间中,并保持曲线上 每个点之间的距离不变,通过自适应地改变输入 信号,将滤波运算降到了一维上,使得域变换滤 波计算复杂度不受相关参数影响,因此,DTRF 在 保持图像边缘的同时,具有实时性的优点。 本文 在提出的 MNSDFB 变换基础上,提出了结合修改 空间频率的域变换递归滤波的多聚焦图像融合 方法。 1 域变换递归滤波 Gastal [11]在域变换基础上提出了边缘保持平滑 递归滤波器(DTRF),它的基本思路可以理解为先 降低输入信号的维数再进行低维滤波。 在五维空间 中,一个边缘保持的平滑滤波可以定义成一个空间 不变的核 H ,它的响应会随着像素点间距离的变化 而变化,如果在某个低维空间中这些距离保持不变, 那么核的响应也将保持不变,因而,达到了保留图像 边缘的目的[11] 。 DTRF 首先将输入信号 I 变换到变 换域 Ωω ,随后,变换域信号由递归滤波器(recursive filter, RF)进行处理如下: J[m] = (1 - a b )I[m] + a b J[m - 1] (1) 式中: J[ m] 是 滤 波 后 的 结 果, 反 馈 系 数 a = exp( - 2 / δs) ∈ [ 0,1] , δs 是 空 间 参 数; I[ m] = I[ xm ] 为输入的离散信号。 b 是变换域 ΩW 相邻采 样 点 xm 和 xm - 1 之 间 的 距 离,可 以 由 b = ct( xm ) - ct( xm - 1 ) 计算得到。 对于变换域信 号 I( x) , ct( u) 可以由式( 2)得到 ct(u) = ∫ u 0 1 + δs δr I′(x) dx,u ∈ Ωw (2) 式中: I′(x) 是 I(x) 的导数, δs 和分别是 DTRF 的 空间参数和范围参数。 由式(2) 可知:随着 b 的增 大, a b 趋近于零,这逐渐使得式(2) 的递归过程收 敛,使得滤波后输出结果中同一侧图像边缘的像素 会取得相近的值,不同侧图像边缘的像素会有很大 差别,从而图像的边缘可以更好地保留下来。 2 融合方法 2.1 组合多小波与 NSDFB 变换 非子采样 Contourlet 变换中首先对图像进行非 子采样塔式分解,然后进行非子采样方向分解(NS⁃ DFB),从而建立了图像的多尺度、多方向的表示。 根据 NSCT 的想法,本文利用多小波将图像分解为 一个低频系数和 3 个高频系数,然后利用 NSDFB 将 4 个高频系数进行 NSDFB 方向分解。 低频系数可 以再次进行多小波分解,并再次对产生的高频系数, ·242· 智 能 系 统 学 报 第 11 卷
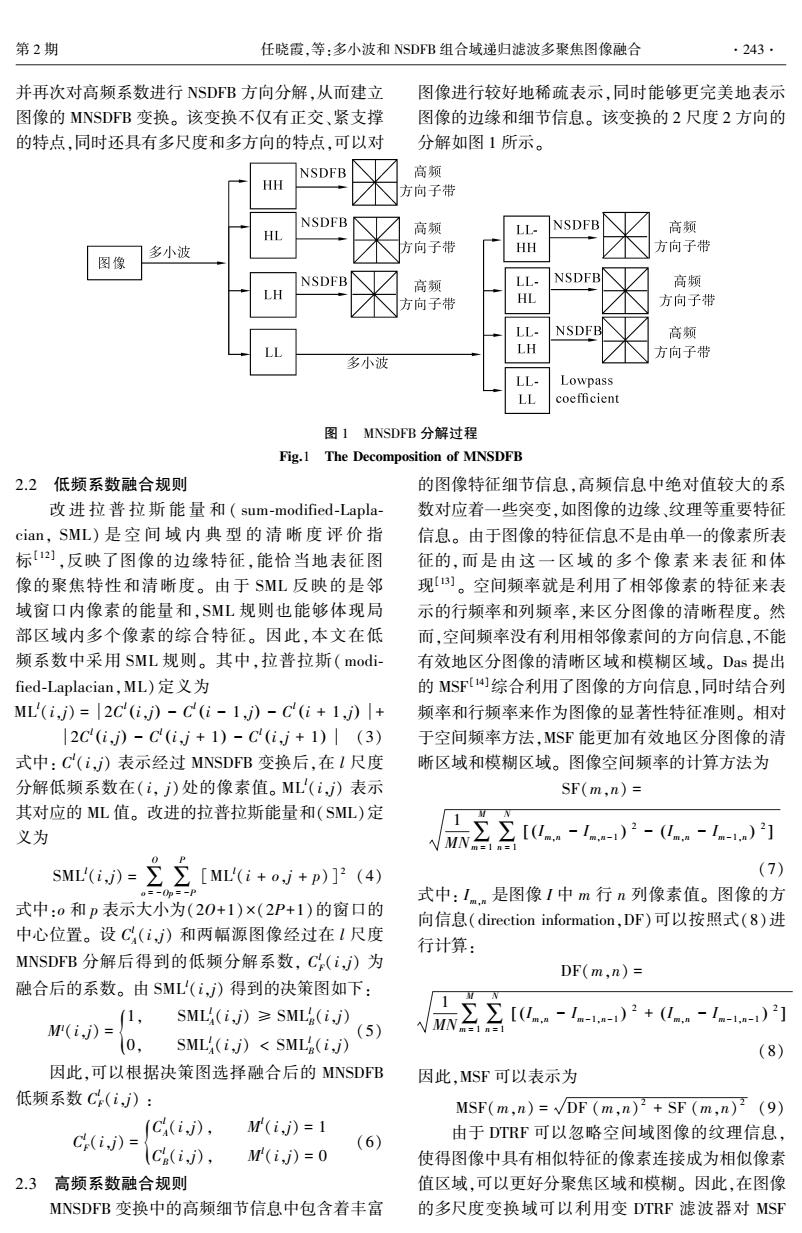
第2期 任晓霞,等:多小波和NSDFB组合域递归滤波多聚焦图像融合 ·243. 并再次对高频系数进行NSDFB方向分解,从而建立 图像进行较好地稀疏表示,同时能够更完美地表示 图像的MNSDFB变换。该变换不仅有正交、紧支撑 图像的边缘和细节信息。该变换的2尺度2方向的 的特点,同时还具有多尺度和多方向的特点,可以对 分解如图1所示。 NSDFB 高频 HH 方向子带 NSDFB HL 高频 LL- NSDEB 高频 方向子带 HH 方向子带 图像 多小波 NSDFB 高频 LL- NSDFB 高频 LH 方向子带 HL 方向子带 LL- NSDFB 高频 LH 方向子带 多小波 Lowpass coefficient 图1 MNSDFB分解过程 Fig.1 The Decomposition of MNSDFB 2.2低频系数融合规则 的图像特征细节信息,高频信息中绝对值较大的系 改进拉普拉斯能量和(sum-modified-Lapla- 数对应着一些突变,如图像的边缘、纹理等重要特征 cian,SML)是空间域内典型的清晰度评价指 信息。由于图像的特征信息不是由单一的像素所表 标【),反映了图像的边缘特征,能恰当地表征图 征的,而是由这一区域的多个像素来表征和体 像的聚焦特性和清晰度。由于SML反映的是邻 现)。空间频率就是利用了相邻像素的特征来表 域窗口内像素的能量和,SML规则也能够体现局 示的行频率和列频率,来区分图像的清晰程度。然 部区域内多个像素的综合特征。因此,本文在低 而,空间频率没有利用相邻像素间的方向信息,不能 频系数中采用SML规则。其中,拉普拉斯(modi- 有效地区分图像的清晰区域和模糊区域。Das提出 fied-Laplacian,ML)定义为 的MSF14)综合利用了图像的方向信息,同时结合列 ML'(i,j)=|2C(i,》-C(i-1,)-C(i+1,)|+ 频率和行频率来作为图像的显著性特征准则。相对 |2c(i,)-C(i,j+1)-C(i,j+1)|(3) 于空间频率方法,MSF能更加有效地区分图像的清 式中:C(i,j)表示经过MNSDFB变换后,在l尺度 晰区域和模糊区域。图像空间频率的计算方法为 分解低频系数在(i,j)处的像素值。ML'(i,)表示 SF(m,n)= 其对应的ML值。改进的拉普拉斯能量和(SML)定 义为 2Au.-1-u.-1 sML(i,)=∑∑[ML'(i+oj+p)]2(4) (7) 0=-0p=-P 式中:Imn是图像I中m行n列像素值。图像的方 式中:0和p表示大小为(20+1)×(2P+1)的窗口的 向信息(direction information,DF)可以按照式(8)进 中心位置。设C(i,)和两幅源图像经过在1尺度 行计算: MNSDFB分解后得到的低频分解系数,C(i,j)为 DF(m,n)= 融合后的系数。由SML'(i,)得到的决策图如下: 1, SML(i,j)≥SML6(i,j) M(i,j)= (5) /日Σ∑[0a-1-a-i)2+0.-1-1-)2 0, SML(i,j)<SMLe(i,j) (8) 因此,可以根据决策图选择融合后的MNSDFB 因此,MSF可以表示为 低频系数C(i,j): MSF(m,n)=DF (m,n)2+SF (m,n)2 (9) (CA(ij), M(i,j)=1 Cr(i,j)= 由于DTRF可以忽略空间域图像的纹理信息, (6) \C(ij), M'(i,j)=0 使得图像中具有相似特征的像素连接成为相似像素 2.3高频系数融合规则 值区域,可以更好分聚焦区域和模糊。因此,在图像 MNSDFB变换中的高频细节信息中包含着丰富 的多尺度变换域可以利用变DTRF滤波器对MSF
并再次对高频系数进行 NSDFB 方向分解,从而建立 图像的 MNSDFB 变换。 该变换不仅有正交、紧支撑 的特点,同时还具有多尺度和多方向的特点,可以对 图像进行较好地稀疏表示,同时能够更完美地表示 图像的边缘和细节信息。 该变换的 2 尺度 2 方向的 分解如图 1 所示。 图 1 MNSDFB 分解过程 Fig.1 The Decomposition of MNSDFB 2.2 低频系数融合规则 改 进 拉 普 拉 斯 能 量 和 ( sum⁃modified⁃Lapla⁃ cian, SML) 是 空 间 域 内 典 型 的 清 晰 度 评 价 指 标[ 12] ,反映了图像的边缘特征,能恰当地表征图 像的聚焦特性和清晰度。 由于 SML 反映的是邻 域窗口内像素的能量和,SML 规则也能够体现局 部区域内多个像素的综合特征。 因此,本文在低 频系数中采用 SML 规则。 其中,拉普拉斯( modi⁃ fied⁃Laplacian,ML)定义为 ML l (i,j) = 2C l (i,j) - C l (i - 1,j) - C l (i + 1,j) + 2C l (i,j) - C l (i,j + 1) - C l (i,j + 1) (3) 式中: C l (i,j) 表示经过 MNSDFB 变换后,在 l 尺度 分解低频系数在( i, j)处的像素值。 ML l (i,j) 表示 其对应的 ML 值。 改进的拉普拉斯能量和(SML)定 义为 SML l (i,j) = ∑ O o = -O∑ P p = -P [ML l (i + o,j + p)] 2 (4) 式中:o 和 p 表示大小为(2O+1) ×(2P+1)的窗口的 中心位置。 设 C l A(i,j) 和两幅源图像经过在 l 尺度 MNSDFB 分解后得到的低频分解系数, C l F(i,j) 为 融合后的系数。 由 SML l (i,j) 得到的决策图如下: Ml(i,j) = 1, SML l A(i,j) ≥ SML l B(i,j) 0, SML l A(i,j) < SML l { B(i,j) (5) 因此,可以根据决策图选择融合后的 MNSDFB 低频系数 C l F(i,j) : C l F(i,j) = C l A(i,j), M l (i,j) = 1 C l B(i,j), M l { (i,j) = 0 (6) 2.3 高频系数融合规则 MNSDFB 变换中的高频细节信息中包含着丰富 的图像特征细节信息,高频信息中绝对值较大的系 数对应着一些突变,如图像的边缘、纹理等重要特征 信息。 由于图像的特征信息不是由单一的像素所表 征的,而 是 由 这 一 区 域 的 多 个 像 素 来 表 征 和 体 现[13] 。 空间频率就是利用了相邻像素的特征来表 示的行频率和列频率,来区分图像的清晰程度。 然 而,空间频率没有利用相邻像素间的方向信息,不能 有效地区分图像的清晰区域和模糊区域。 Das 提出 的 MSF [14]综合利用了图像的方向信息,同时结合列 频率和行频率来作为图像的显著性特征准则。 相对 于空间频率方法,MSF 能更加有效地区分图像的清 晰区域和模糊区域。 图像空间频率的计算方法为 SF(m,n) = 1 MN∑ M m = 1∑ N n = 1 Im,n - Im,n-1 ( ) 2 - Im,n - Im-1,n ( ) 2 [ ] (7) 式中: Im,n 是图像 I 中 m 行 n 列像素值。 图像的方 向信息(direction information,DF)可以按照式(8)进 行计算: DF(m,n) = 1 MN∑ M m = 1∑ N n = 1 Im,n - Im-1,n-1 ( ) 2 + Im,n - Im-1,n-1 ( ) 2 [ ] (8) 因此,MSF 可以表示为 MSF(m,n) = DF (m,n) 2 + SF (m,n) 2 (9) 由于 DTRF 可以忽略空间域图像的纹理信息, 使得图像中具有相似特征的像素连接成为相似像素 值区域,可以更好分聚焦区域和模糊。 因此,在图像 的多尺度变换域可以利用变 DTRF 滤波器对 MSF 第 2 期 任晓霞,等:多小波和 NSDFB 组合域递归滤波多聚焦图像融合 ·243·
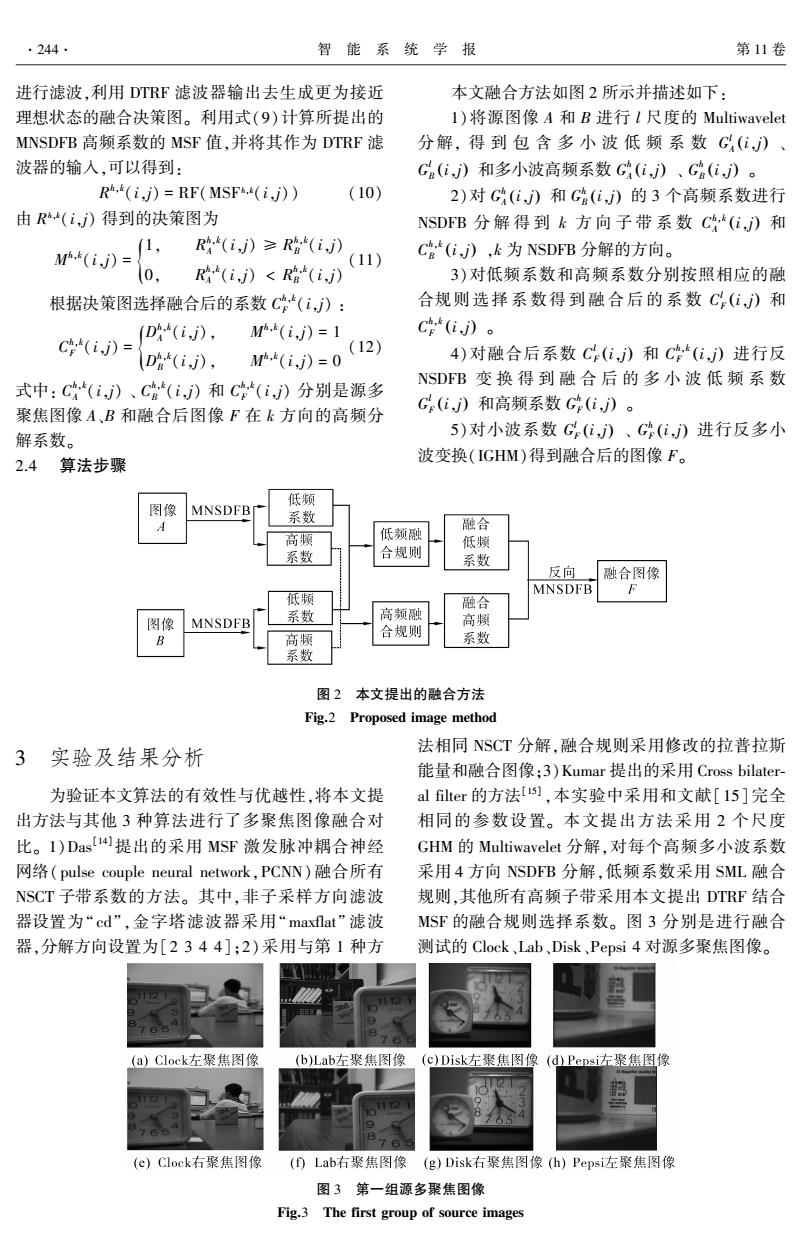
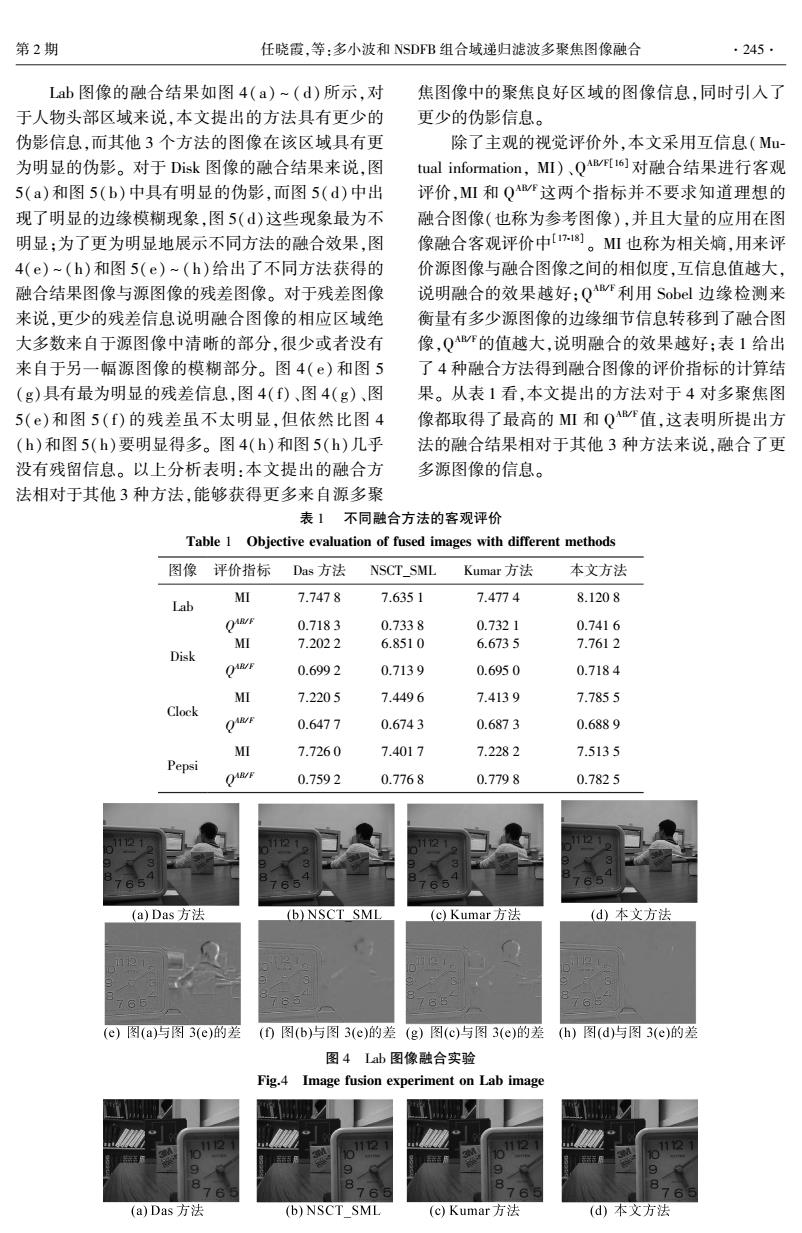
.244 智能系统学报 第11卷 进行滤波,利用DTRF滤波器输出去生成更为接近 本文融合方法如图2所示并描述如下: 理想状态的融合决策图。利用式(9)计算所提出的 l)将源图像A和B进行l尺度的Multiwavelet MNSDFB高频系数的MSF值,并将其作为DTRF滤 分解,得到包含多小波低频系数G(i,)、 波器的输人,可以得到: G(i》和多小波高频系数G(i》、G哈(i》。 R(i,j)=RF(MSF(i,j)) (10) 2)对G(i,)和G(i,》的3个高频系数进行 由R(i,)得到的决策图为 NSDB分解得到k方向子带系数C.(i,)和 1, R(i,j》≥R.(i,i) M(i.j)= (11) C.(i,),k为NSDFB分解的方向。 0 R(i,》<R路(i,) 3)对低频系数和高频系数分别按照相应的融 根据决策图选择融合后的系数C,(i,》: 合规则选择系数得到融合后的系数C(i,)和 D,(i,j), M(i,j)=1 C(ij》。 C(i,j》= (12) D(ij). ,(i,j)=0 4)对融合后系数C(i,)和C(i,)进行反 NSDFB变换得到融合后的多小波低频系数 式中:C,(i,》、C.(i,)和C(i,》分别是源多 聚焦图像A、B和融合后图像F在k方向的高频分 G(i,)和高频系数G(i,)。 解系数。 5)对小波系数G(i,)、G(i,)进行反多小 2.4 算法步骤 波变换(IGHM)得到融合后的图像F。 低频 图像 MNSDFB 系数 A 融合 高撅 低颜融 合规则 低频 系数 系数 反向 融合图像 MNSDFB F 低频 融合 高频融 图像 MNSDFB 系数 高频 B 高频 合规则 系数 系数 图2本文提出的融合方法 Fig.2 Proposed image method 3实验及结果分析 法相同NSCT分解,融合规则采用修改的拉普拉斯 能量和融合图像:3)Kumar提出的采用Cross bilater- 为验证本文算法的有效性与优越性,将本文提 al filter的方法1s),本实验中采用和文献[l5]完全 出方法与其他3种算法进行了多聚焦图像融合对 相同的参数设置。本文提出方法采用2个尺度 比。1)Das提出的采用MSF激发脉冲耦合神经 GHM的Multiwavelet分解,对每个高频多小波系数 网络(pulse couple neural network,PCNN)融合所有 采用4方向NSDFB分解,低频系数采用SML融合 NSCT子带系数的方法。其中,非子采样方向滤波 规则,其他所有高频子带采用本文提出DTRF结合 器设置为“cd”,金字塔滤波器采用“maxflat”滤波 MSF的融合规则选择系数。图3分别是进行融合 器,分解方向设置为[2344]:2)采用与第1种方 测试的Clock、Lab、Disk、Pepsi4对源多聚焦图像。 a)Clock左聚焦图像 (b)Lab左聚焦图像(c)Disk左聚焦图像(d)Pepsi左聚焦图像 (e)Clock右聚焦图像 (DLab右聚焦图像 (g)Disk右聚焦图像(h)Pepsiz左聚焦图像 图3第一组源多聚焦图像 Fig.3 The first group of source images
进行滤波,利用 DTRF 滤波器输出去生成更为接近 理想状态的融合决策图。 利用式(9)计算所提出的 MNSDFB 高频系数的 MSF 值,并将其作为 DTRF 滤 波器的输入,可以得到: R h,k (i,j) = RF(MSF h,k(i,j)) (10) 由 R h,k(i,j) 得到的决策图为 M h,k (i,j) = 1, R h,k A (i,j) ≥ R h,k B (i,j) 0, R h,k A (i,j) < R h,k { B (i,j) (11) 根据决策图选择融合后的系数 C h,k F (i,j) : C h,k F (i,j) = D h,k A (i,j), M h,k (i,j) = 1 D h,k B (i,j), M h,k { (i,j) = 0 (12) 式中: C h,k A (i,j) 、 C h,k B (i,j) 和 C h,k F (i,j) 分别是源多 聚焦图像 A、B 和融合后图像 F 在 k 方向的高频分 解系数。 2.4 算法步骤 本文融合方法如图 2 所示并描述如下: 1)将源图像 A 和 B 进行 l 尺度的 Multiwavelet 分解, 得 到 包 含 多 小 波 低 频 系 数 G l A (i,j) 、 G l B (i,j) 和多小波高频系数 G h A (i,j) 、 G h B (i,j) 。 2)对 G h A (i,j) 和 G h B (i,j) 的 3 个高频系数进行 NSDFB 分 解 得 到 k 方 向 子 带 系 数 C h,k A (i,j) 和 C h,k B (i,j) ,k 为 NSDFB 分解的方向。 3)对低频系数和高频系数分别按照相应的融 合规则 选 择 系 数 得 到 融 合 后 的 系 数 C l F (i,j) 和 C h,k F (i,j) 。 4)对融合后系数 C l F (i,j) 和 C h,k F (i,j) 进行反 NSDFB 变 换 得 到 融 合 后 的 多 小 波 低 频 系 数 G l F (i,j) 和高频系数 G h F (i,j) 。 5)对小波系数 G l F (i,j) 、 G h F (i,j) 进行反多小 波变换(IGHM)得到融合后的图像 F。 图 2 本文提出的融合方法 Fig.2 Proposed image method 3 实验及结果分析 为验证本文算法的有效性与优越性,将本文提 出方法与其他 3 种算法进行了多聚焦图像融合对 比。 1)Das [14]提出的采用 MSF 激发脉冲耦合神经 网络( pulse couple neural network,PCNN) 融合所有 NSCT 子带系数的方法。 其中,非子采样方向滤波 器设置为“ cd”,金字塔滤波器采用“ maxflat” 滤波 器,分解方向设置为[2 3 4 4];2)采用与第 1 种方 法相同 NSCT 分解,融合规则采用修改的拉普拉斯 能量和融合图像;3)Kumar 提出的采用 Cross bilater⁃ al filter 的方法[15] ,本实验中采用和文献[15] 完全 相同的参数设置。 本文提出方法采用 2 个尺度 GHM 的 Multiwavelet 分解,对每个高频多小波系数 采用 4 方向 NSDFB 分解,低频系数采用 SML 融合 规则,其他所有高频子带采用本文提出 DTRF 结合 MSF 的融合规则选择系数。 图 3 分别是进行融合 测试的 Clock、Lab、Disk、Pepsi 4 对源多聚焦图像。 图 3 第一组源多聚焦图像 Fig.3 The first group of source images ·244· 智 能 系 统 学 报 第 11 卷
第2期 任晓霞,等:多小波和NSDFB组合域递归滤波多聚焦图像融合 .245. Lab图像的融合结果如图4(a)~(d)所示,对 焦图像中的聚焦良好区域的图像信息,同时引入了 于人物头部区域来说,本文提出的方法具有更少的 更少的伪影信息。 伪影信息,而其他3个方法的图像在该区域具有更 除了主观的视觉评价外,本文采用互信息(M如 为明显的伪影。对于Disk图像的融合结果来说,图 tual information,MI)、Qv[6]对融合结果进行客观 5(a)和图5(b)中具有明显的伪影,而图5(d)中出 评价,M和QA这两个指标并不要求知道理想的 现了明显的边缘模糊现象,图5()这些现象最为不 融合图像(也称为参考图像),并且大量的应用在图 明显:为了更为明显地展示不同方法的融合效果,图 像融合客观评价中718)。M也称为相关嫡,用来评 4(e)~(h)和图5(e)~(h)给出了不同方法获得的 价源图像与融合图像之间的相似度,互信息值越大, 融合结果图像与源图像的残差图像。对于残差图像 说明融合的效果越好;Qr利用Sobel边缘检测来 来说,更少的残差信息说明融合图像的相应区域绝 衡量有多少源图像的边缘细节信息转移到了融合图 大多数来自于源图像中清晰的部分,很少或者没有 像,Q的值越大,说明融合的效果越好:表1给出 来自于另一幅源图像的模糊部分。图4(e)和图5 了4种融合方法得到融合图像的评价指标的计算结 (g)具有最为明显的残差信息,图4(f)、图4(g)、图 果。从表1看,本文提出的方法对于4对多聚焦图 5(e)和图5(f)的残差虽不太明显,但依然比图4 像都取得了最高的I和Q值,这表明所提出方 (h)和图5(h)要明显得多。图4(h)和图5(h)几乎 法的融合结果相对于其他3种方法来说,融合了更 没有残留信息。以上分析表明:本文提出的融合方 多源图像的信息。 法相对于其他3种方法,能够获得更多来自源多聚 表1不同融合方法的客观评价 Table 1 Objective evaluation of fused images with different methods 图像评价指标Das方法 NSCT SML Kumar方法 本文方法 MI 7.7478 7.6351 7.4774 8.1208 Lab OARVE 0.7183 0.7338 0.7321 0.7416 MI 7.2022 6.8510 6.6735 7.7612 Disk OARIF 0.6992 0.7139 0.6950 0.7184 MI 7.2205 7.4496 7.4139 7.7855 Clock OE 0.6477 0.6743 0.6873 0.6889 MI 7.7260 7.4017 7.2282 7.5135 Pepsi OARVE 0.7592 0.7768 0.7798 0.7825 (a)Das方法 (b)NSCT SMI (c)Kumar方法 (d)本文方法 (e)图(a)与图3(e)的差 ()图(b)与图3(e)的差(g)图(c)与图3(e)的差(h)图(d)与图3(e)的差 图4Lb图像融合实验 Fig.4 Image fusion experiment on Lab image 76 (a)Das方法 (b)NSCT SML (c)Kumar方法 (d)本文方法
Lab 图像的融合结果如图 4( a) ~ ( d) 所示,对 于人物头部区域来说,本文提出的方法具有更少的 伪影信息,而其他 3 个方法的图像在该区域具有更 为明显的伪影。 对于 Disk 图像的融合结果来说,图 5(a)和图 5(b)中具有明显的伪影,而图 5(d)中出 现了明显的边缘模糊现象,图 5(d)这些现象最为不 明显;为了更为明显地展示不同方法的融合效果,图 4(e) ~ (h)和图 5( e) ~ ( h)给出了不同方法获得的 融合结果图像与源图像的残差图像。 对于残差图像 来说,更少的残差信息说明融合图像的相应区域绝 大多数来自于源图像中清晰的部分,很少或者没有 来自于另一幅源图像的模糊部分。 图 4( e) 和图 5 (g)具有最为明显的残差信息,图 4(f)、图 4(g)、图 5(e)和图 5( f) 的残差虽不太明显,但依然比图 4 (h)和图 5(h)要明显得多。 图 4(h)和图 5(h)几乎 没有残留信息。 以上分析表明:本文提出的融合方 法相对于其他 3 种方法,能够获得更多来自源多聚 焦图像中的聚焦良好区域的图像信息,同时引入了 更少的伪影信息。 除了主观的视觉评价外,本文采用互信息(Mu⁃ tual information, MI)、Q AB/ F[16] 对融合结果进行客观 评价,MI 和 Q AB/ F这两个指标并不要求知道理想的 融合图像(也称为参考图像),并且大量的应用在图 像融合客观评价中[17⁃18] 。 MI 也称为相关熵,用来评 价源图像与融合图像之间的相似度,互信息值越大, 说明融合的效果越好;Q AB/ F利用 Sobel 边缘检测来 衡量有多少源图像的边缘细节信息转移到了融合图 像,Q AB/ F的值越大,说明融合的效果越好;表 1 给出 了 4 种融合方法得到融合图像的评价指标的计算结 果。 从表 1 看,本文提出的方法对于 4 对多聚焦图 像都取得了最高的 MI 和 Q AB/ F值,这表明所提出方 法的融合结果相对于其他 3 种方法来说,融合了更 多源图像的信息。 表 1 不同融合方法的客观评价 Table 1 Objective evaluation of fused images with different methods 图像 评价指标 Das 方法 NSCT_SML Kumar 方法 本文方法 Lab MI 7.747 8 7.635 1 7.477 4 8.120 8 Q AB/ F 0.718 3 0.733 8 0.732 1 0.741 6 Disk MI 7.202 2 6.851 0 6.673 5 7.761 2 Q AB/ F 0.699 2 0.713 9 0.695 0 0.718 4 Clock MI 7.220 5 7.449 6 7.413 9 7.785 5 Q AB/ F 0.647 7 0.674 3 0.687 3 0.688 9 Pepsi MI 7.726 0 7.401 7 7.228 2 7.513 5 Q AB/ F 0.759 2 0.776 8 0.779 8 0.782 5 图 4 Lab 图像融合实验 Fig.4 Image fusion experiment on Lab image 第 2 期 任晓霞,等:多小波和 NSDFB 组合域递归滤波多聚焦图像融合 ·245·