
理想场的标准运动方程在有限长、区间常数场元件内的解至 此已告解决 使用这3个形式上统一的函数,给书写各种表达式和计算机 程序计算带来很多方便.不仅粒子的轨迹,后文要谈到的色散函数 门、包络函数3等在这种有限长的区间常数场元件内的解析式都可 以用这3个函数组成的统一表达式给出,计算它们的平均值(利用 有关积分公式)也很方便.在磁铁系统设计计算时,常用到传输矩 阵元对聚焦强度F或元件长度L的微商,前面已给出了它们的 不依赖于F,符号的统一表达式(对L的微商就是各函数对之的 微商):这些函数和微商即使当F,需要变符号时也是连续的.一 个很短小精悍的子程序就能完成所有的“厚器件”传输矩阵或该矩 阵对F、对L的变化率的计算.只要告诉该子程序3个变量 F,G和L,矩阵行列数,以及使用者需要的是什么一传输矩阵 本身还是它对变量F.或对L的变化率,它就能完成任务,无论所 处理的是弯铁(包括非弯转平面)、四极磁铁还是漂移段
17

当G=0时,意味着无弯转:G“>0时是正弯转(水平面向内、 铅垂面向上);G<0时是负弯转.当F>0时为聚焦元件;F<0 时为散焦元件;F,=0时则在相应平面内是漂移段.L一般自然大 于0:如果L<0,得到的是一个逆矩阵,相当于倒退一段距离的传 输,也就是说,M(一L)总等于[M(L)]1;当L=0时,无论其他参 数如何,给出的传输矩阵都是单位阵 “无长度元件”的薄透镜传输矩阵是容易给出的.具体形式应 针对不同的场(可能是非理想场)再“见景生情”.一般而言,应该用 6×6阶矩阵,它的所有对角线元素都是1:第1行、第3行的其他 元素都是0(位置不变):其他则可能有若干个为数不多的非0项, 18
18
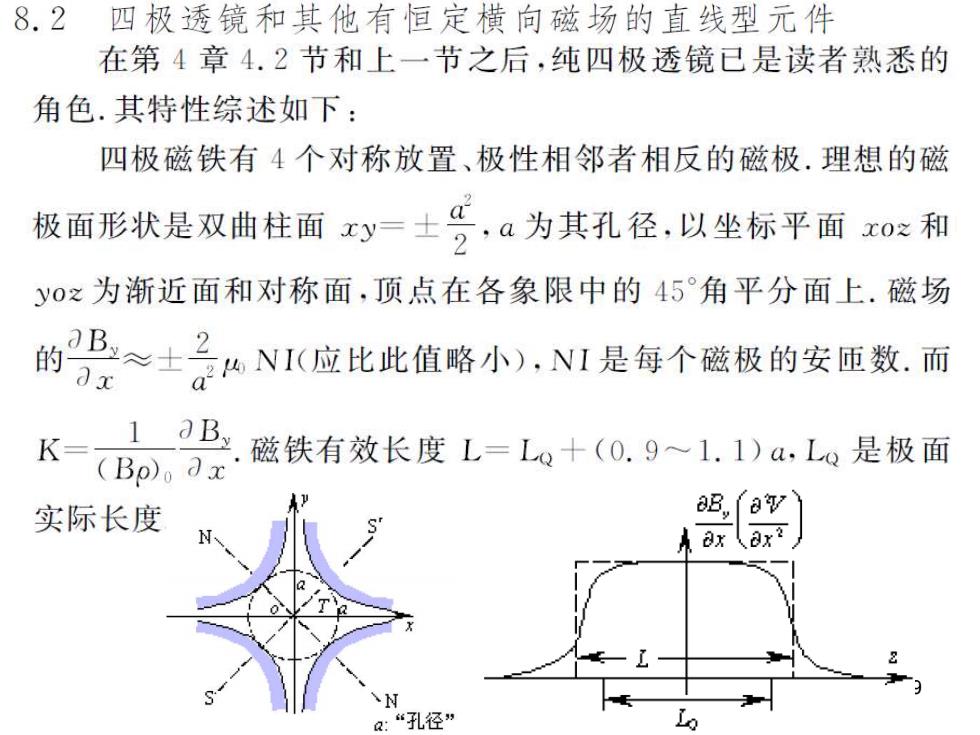
8.2四极透镜和其他有恒定横向磁场的直线型元件 在第4章4.2节和上一节之后,纯四极透镜已是读者熟悉的 角色.其特性综述如下: 四极磁铁有4个对称放置、极性相邻者相反的磁极.理想的磁 极面形状是双曲柱面xy= 号a为其孔径,以坐标平面x0和 y0之为渐近面和对称面,顶点在各象限中的45°角平分面上.磁场 B≈士二4NI(应比此值略小),N1是每个磁极的安匝数.而 的 2 1 K aB (Bo)o ax .磁铁有效长度L=Lo十(0.9~1.1)a,Lo是极面 实际长度 B 8x? N a:“孔径” o
19

四极磁铁中的粒子运动方程为 u"+Fu=0 6 +F()·u=X)·& = X·u+9 式中,Fx=一Fy=K 四极磁铁中运动方程的解为 u(z)=u·C(之-x)+u′·Su(之一z) u'(z)=-u·FuS(x-)十w′·Cu(之- m m12m13m14 m15m16 C,(L) S,(L) 0 0007 x mzi m22 m23m24 1m25 m26 -F,S,(L)C,(L) 0 000 m31 m32 m34 m35 m36 0 0 m33 y C,(L) S,(L)00 0 0 v" -F,S,(L)C,(L)00 m41 m42 m44 mas m46 y L m51 ms2 m54 mss ms6 Zd 0 0 0 0 1 6 m61m62 n63 m64 m65 m66 0 0 0 0 01J 20
20 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 1 0 61 62 63 64 65 66 d d x x m m m m m m x x m m m m m m y y m m m m m m y y m m m m m m z z m m m m m m m m m m m m = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 x x x x x y y y y y C L S L F S L C L C L S L F S L C L L − −

在聚焦平面上F>O0,于是 C.(z)=cos(VFz) F.=K十G2 sin(F z) Fy=-K+Gy2 S(x)= VF. K- 1 aB 在散焦平面上F<0,于是 (Bo)。 Gr- 1 C.()=ch(Fz) Px (Bo)o S(x)= sh(-Faz) G= 1 B VF Py (Bo)0 因为G=0,四极透镜的,=0,它不能产生色散,但束流已有 的色散会因其聚散焦作用而变小或变大.下一章将谈到,它也不能 把色散完全消除 21
21