
这些典型元器件可分成两大类,以便进行数学处理.一类是 “有限长度器件”,或称“厚器件”,其中的场假设满足“区间常数”条 件,可逐元件地用解析法计算各元件对应的传输矩阵.另一类是 “无长度器件”,即薄透镜,其中的场可用“冲量假设”处理,对应的 传输矩阵就是“元传输矩阵”,但对若干可看作♂函数的量求积分. 之所以如此,可能是因为其作用区间确实很短,也可能因为其相对 强度较弱,可以把该场看作微扰,更准确的数学处理有难度或无 必要 大多数“有限长度器件”中的粒子运动方程就是上一章中的理 想场标准运动方程: "+Fu(z)·u=Gu()·δ z'=-G(》·u+ d 式中,u=x或y.F,G在有效长度L内(≤≤十L)视为常 数,其含义见前文
7

F-K+G ”+F.·u=Gw·8 Fy=-K+G2 '=-(G.·x+G,·y)+8 K- 1 ∂B (Bo)。axJo G=1 By (Bo)o G=一1 B Py (B0) 上一章已论述过,前一方程的通解应能写成u=·w十u ·十δ·和这3个数学特解函数,s,的性质,包括它们 满足的方程和初始条件. 为寻求各特解函数在区间常数条件下的数学形式,不妨根据 其初始条件与参量F.和G都不随之变化的特点,用级数展开法 求解.其结果可写成如下3个特殊函数:
8
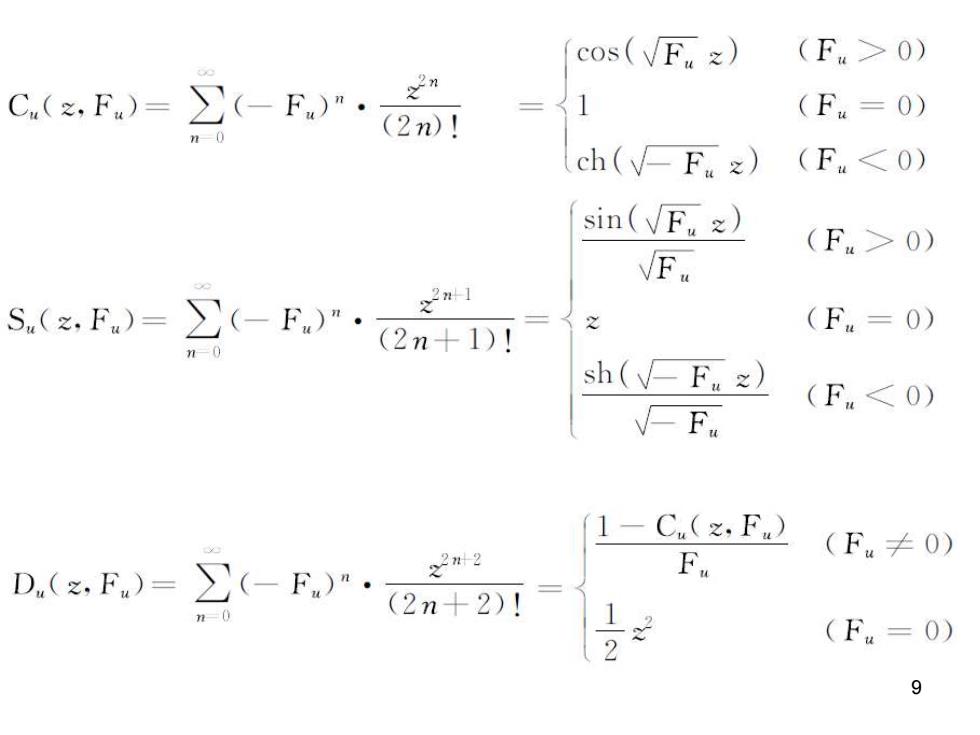
cos(Fz) (F.>0) C)=(-· (F4=0) ch(v F z)(F<0) sin(Fz) (F.>0) F s)=-R·g (Fu=0) sh(-Faz) (F.<0)》 F 1-C(,Fw) 222 D.(xF.)=(-F.)·2n+2 F (F.≠0) (Fu=0) 9
9

上述3个函数的命名与基本性质如下: Cw为“似余弦函数”,满足 C"+F.·Cw=0 C.(0)=1 Cw'(0)=0 S,为“似正弦函数”,满足 S"+F.·S4=0 S.(0)=0 S.'(0)=1 D为“色散发生函数”,满足 D"+F.·Dw=1 D(0)=0 D.'(0)=0 10
10

由此可见,这3个特殊函数都具有满足某一特定条件的最基 本单元的意味.考虑到复变函数论中三角函数和双曲三角函数的 关系及当~或F,趋于0时求极限,每个特殊函数尽管当F,取不 同值时有不同写法,或曰需用不同的计算方法求值,事实上各是一 个“统一”的函数,而且对F的变化都是连续的. 3个函数皆以之为第一自变量,F为第二自变量或参变量, 所以,如后面括号内只写一个自变量,就意味着它是之,而且“”代 表对之微分.Cm无量纲,S.与D.的单位分别是m和m(方程参 量Fu,G.的单位分别是m2和m1).容易看到,Cu与D是之的 偶函数,S是之的奇函数.它们还有以下性质: 基本恒等式: Cw2+Fk·Sw2=1 Cu+Fu·Du=1 Sn2=D.(1十Cm) 11
11