
KC从变换编码到单像素相机 ◆漫谈变换编码 ▣为什么不在时域编码而用变换编码? 口傅里叶变换及其变体在应用中遇到的问题 ▣什么是小波变换? ◆CT图像的常识 口CT图像的产生原理 ▣CT图像如何重建? ◆单像素相机 ▣单像素数码相机原理 口压缩感知理论 ◆光场相机 26 ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn 从变换编码到单像素相机 漫谈变换编码 为什么不在时域编码而用变换编码? 傅里叶变换及其变体在应用中遇到的问题 什么是小波变换? CT图像的常识 CT图像的产生原理 CT图像如何重建? 单像素相机 单像素数码相机原理 压缩感知理论 光场相机 26
KC变换:基函数的线性组合 人 傅里叶变换只是用基函数线 性组合表示信号的一种情况 /+∧ 傅里叶变换在整个时间轴上积分,表示了信号的全局特征。 如果需要分析信号的局部信号怎么办? ·定义一组能够表现出信号瞬时性的基函数 Haar小波展开信号→ 1910:Alfred Haar discovers the Haar wavelet ynh.cxh @ustc.edu.cn
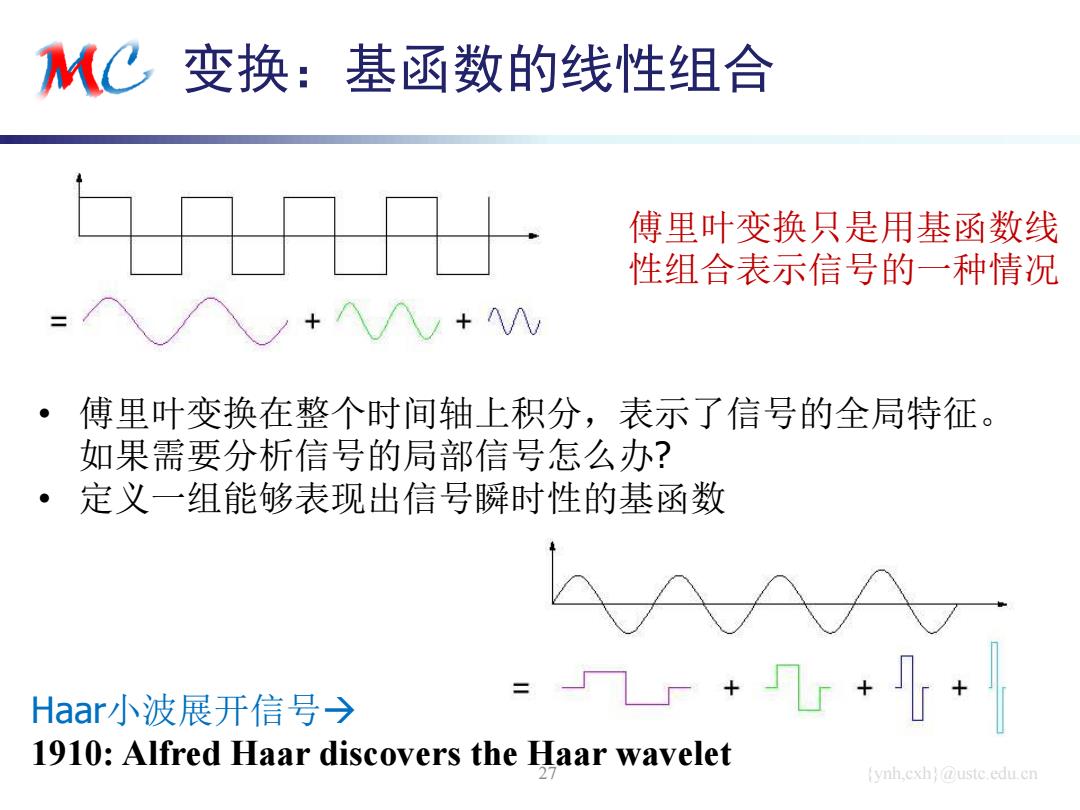
{ynh,cxh}@ustc.edu.cn 变换:基函数的线性组合 27 傅里叶变换只是用基函数线 性组合表示信号的一种情况 Haar小波展开信号 1910: Alfred Haar discovers the Haar wavelet • 傅里叶变换在整个时间轴上积分,表示了信号的全局特征。 如果需要分析信号的局部信号怎么办? • 定义一组能够表现出信号瞬时性的基函数
KC Gabor?变换 窗口傅里叶变换能够完成局部分 Dennis Gabor,1946 析的关键是窗口,当窗函数取为 高斯窗时一般称为Gabor?变换。 G,(a;b,)=f(t)gs(t-b)e idt Aa t);(:b.o)e.(-be doub Gabor?变换在要分析的信号上提取出信号中的每一个小段,将 此小段进行两端周期性延拓,并对这样的信号进行传统傅里 叶分析,得到此小段内信号的频率特性,平移原有分析信号 中小段的位置,得到整个要分析信号在每个小范围内频率成 分。严格地讲gbor变换算不上小波,因为构不成正交基。 ynh.cxh @ustc.edu.cn
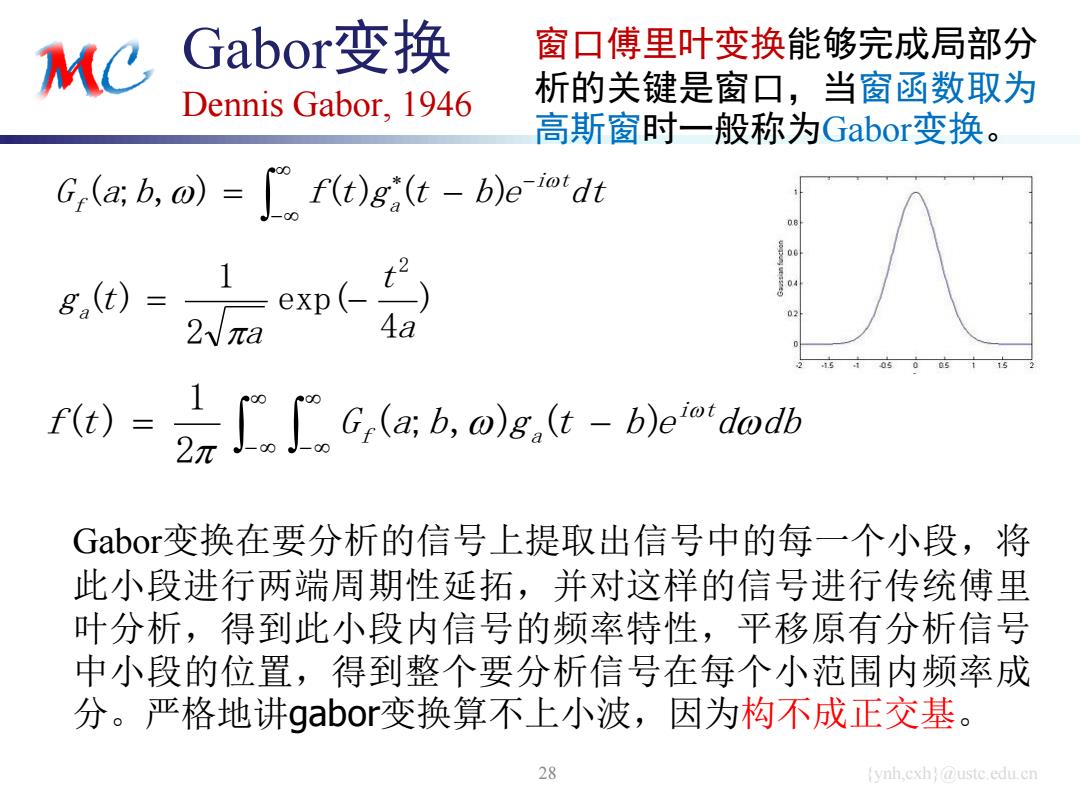
{ynh,cxh}@ustc.edu.cn Gabor变换 Dennis Gabor, 1946 28 G a b f t g t b e dt i t f a ( ; , ) ( ) ( ) ) 4 exp( 2 1 ( ) 2 a t a g a t f t G a b g t b e d db i t f a ( ; , ) ( ) 2 1 ( ) Gabor变换在要分析的信号上提取出信号中的每一个小段,将 此小段进行两端周期性延拓,并对这样的信号进行传统傅里 叶分析,得到此小段内信号的频率特性,平移原有分析信号 中小段的位置,得到整个要分析信号在每个小范围内频率成 分。严格地讲gabor变换算不上小波,因为构不成正交基。 窗口傅里叶变换能够完成局部分 析的关键是窗口,当窗函数取为 高斯窗时一般称为Gabor变换

KC2 D Gabor?变换 G(x,y)=2mo e 02 0.2 2 0 0 -02 成41 2 2 0 0 0 -2 -2 2 4 -2 2 2D Gabor filter functions 1 1 164 S0骨 8 2 02 154554202 0122 0 0 0 0 0 22 -1 2-2 22
{ynh,cxh}@ustc.edu.cn 2D Gabor变换 29 2D Gabor filter functions

C Gabor变换的缺陷 ◆Gabor?在1946年引入了窗口傅里叶变换。该变换自身也 存在不可克服的缺陷,即当窗函数g)确定后,矩形窗口 的形状就已确定。故窗口傅里叶变换在时域具有等时宽/在 频率具有等带宽特性。也就是说,窗口傅里叶变换在视频 平面各处的分辨率相同。 frequency time ◆现在的小波序列:一个基本小波(母小波)经伸缩和平 移得到。常见有Daubechies小波、Symlets.小波、Morlet小 波、Mexican Hat小波等 30 ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn Gabor变换的缺陷 Gabor在1946年引入了窗口傅里叶变换。该变换自身也 存在不可克服的缺陷,即当窗函数g(t)确定后,矩形窗口 的形状就已确定。故窗口傅里叶变换在时域具有等时宽/在 频率具有等带宽特性。也就是说,窗口傅里叶变换在视频 平面各处的分辨率相同。 现在的小波序列:一个基本小波(母小波)经伸缩和平 移得到。常见有Daubechies小波、Symlets小波、Morlet小 波、Mexican Hat小波等。 30