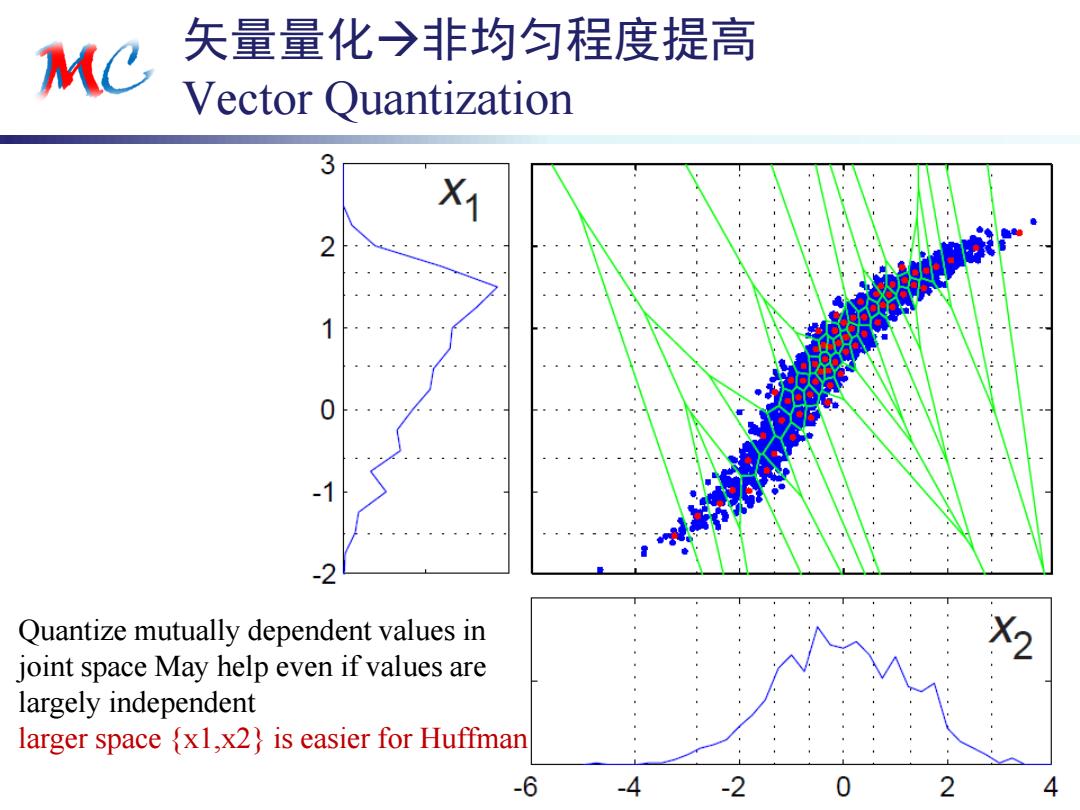
Me 矢量量化→非均匀程度提高 Vector Quantization 3 X1 2 Quantize mutually dependent values in joint space May help even if values are largely independent larger space {x1,x2)is easier for Huffman -6 -4-2 0 2 4
{ynh,cxh}@ustc.edu.cn 矢量量化非均匀程度提高 Vector Quantization 6 Quantize mutually dependent values in joint space May help even if values are largely independent larger space {x1,x2} is easier for Huffman
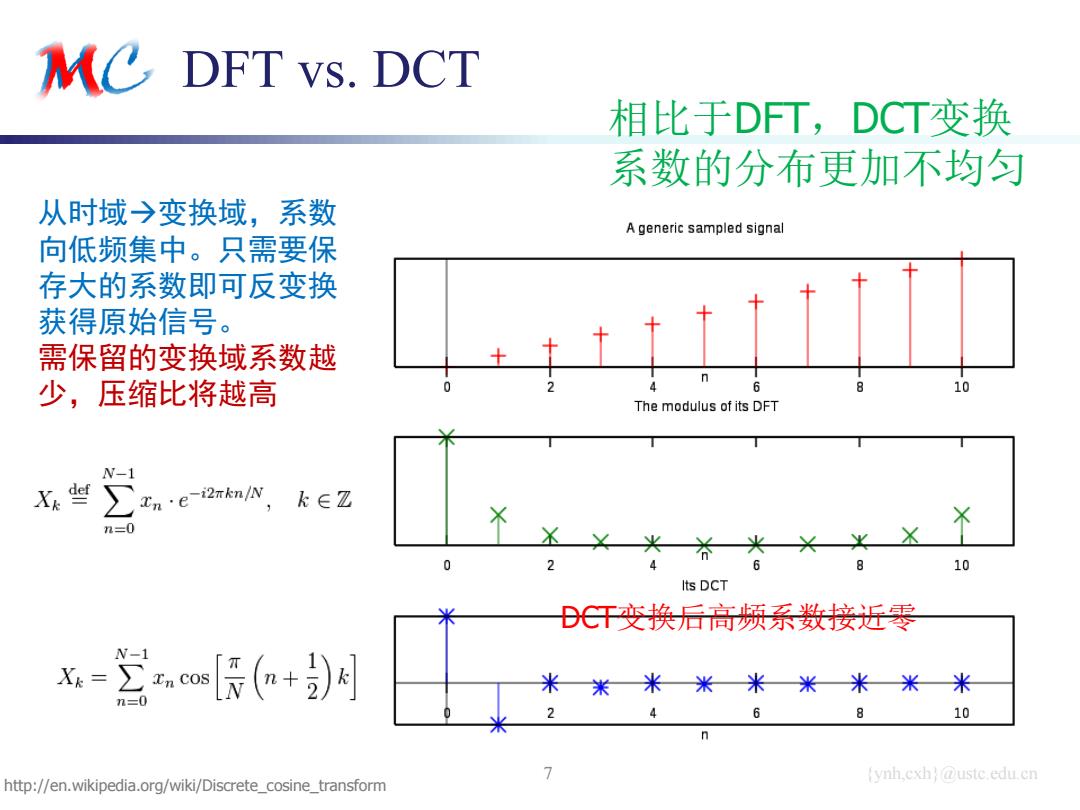
MC DFT vs.DCT 相比于DFT,DCT变换 系数的分布更加不均匀 从时域→变换域,系数 A generic sampled signal 向低频集中。只需要保 存大的系数即可反变换 获得原始信号。 需保留的变换域系数越 少,压缩比将越高 10 The modulus of its DFT N- X些 ∑ne2n,k∈z n=0 0 2 10 Its DCT DC纤变换后高频系数接近零 N-1 Xk= 米米米米米米米米米 n=0 2 6 10 7 ynh.cxh @ustc.edu.cn http://en.wikipedia.org/wiki/Discrete_cosine_transform
{ynh,cxh}@ustc.edu.cn DFT vs. DCT 7 DCT变换后高频系数接近零 http://en.wikipedia.org/wiki/Discrete_cosine_transform 从时域变换域,系数 向低频集中。只需要保 存大的系数即可反变换 获得原始信号。 需保留的变换域系数越 少,压缩比将越高 相比于DFT,DCT变换 系数的分布更加不均匀
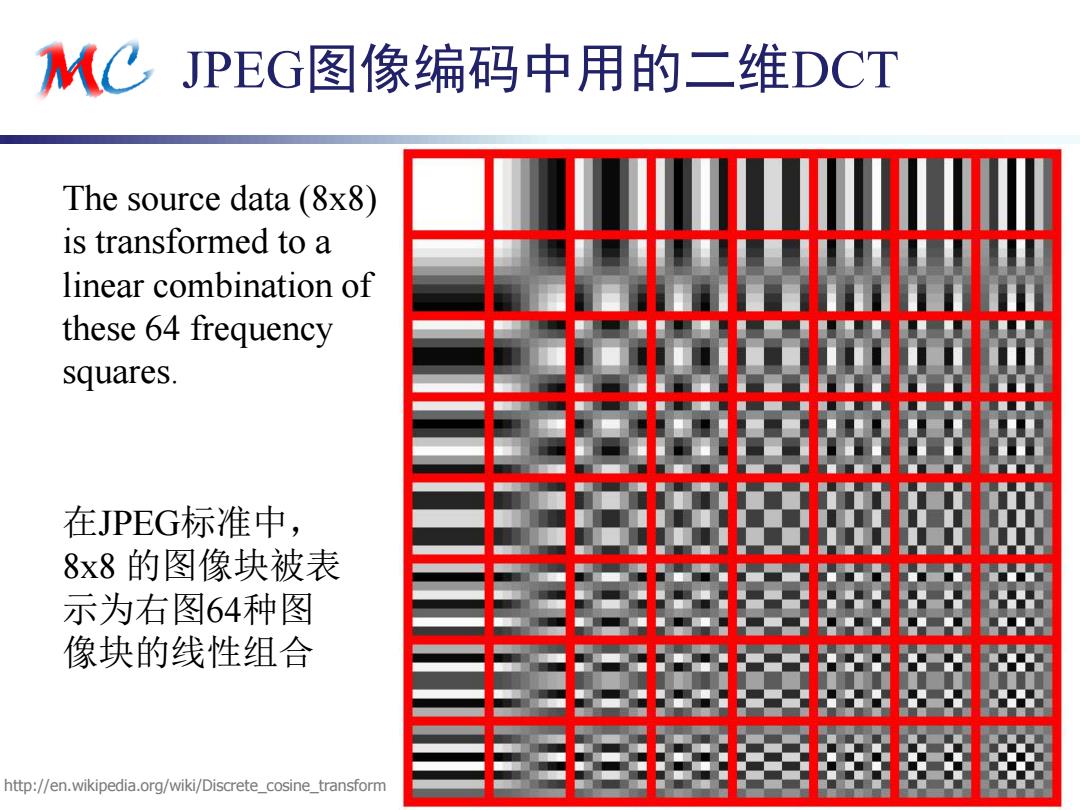
MC JPEG图像编码中用的二维DCT The source data (8x8) is transformed to a linear combination of these 64 frequency squares. 在JPEG标准中, 8x8的图像块被表 示为右图64种图 像块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform
{ynh,cxh}@ustc.edu.cn JPEG图像编码中用的二维DCT 8 The source data (8x8) is transformed to a linear combination of these 64 frequency squares. 在JPEG标准中, 8x8 的图像块被表 示为右图64种图 像块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform

KC二维DCT示例 88 A AA 5.1917 0,3911 1.2418 0.岁2 0.1583 0272 -00729 0,2205 0.02里号 05 0.3947 07846 8x8的原始图像块被 表示为右图64种图像 1,28 02214 4.0017-0.2720 0.789 块的线性组合 -0.2640-0.0392-0,2517 0.2750 00226 ,2183 258 6.1924 0.06580.0428-0,4721 0,29u5 4/95 0,31690054g,468-00225-,00550407-0,465001500 http://en.wikipedia.org/wiki/Discrete_cosine_transform -27四-0627 0196000649-0,4u6-01011749
{ynh,cxh}@ustc.edu.cn 二维DCT示例 9 8x8 的原始图像块被 表示为右图64种图像 块的线性组合 http://en.wikipedia.org/wiki/Discrete_cosine_transform

KC图像压缩中的DCT变换 白色代表大的系数;黑色代表接近零的系数 original DFT DCT ynh.cxh @ustc.edu.cn
{ynh,cxh}@ustc.edu.cn 图像压缩中的DCT变换 10 original DFT DCT 白色代表大的系数;黑色代表接近零的系数