实验8多项式插值 参考答案 L.拉格朗日插值法:function[C,L-lagran(X,Y)(见代码文件) 牛顿插值法:function[C,D=newpoly(X,Y(见代码文件) 5个点确定唯一的4次插值多项式:P4x)5.72916666666652×10x -0.000108333333333332r+0.0068958333333331x2-0.33916666666666r+78.2 Neville算法:function,Q]-Nevile(K_input.y_.input.x,eps)(见代码文件〉 >>polyval(C,30) ans=71.770312500000017 >>polyval(C.55) ans=67.624316406249775 3.(a)求得的5次插值多项式为 Ps(x)=0.0166666666666675x.0.291666666666657x+2x -6.70833333333303249.98333333333358x+61 (b)霍纳算法就是嵌套乘法,在对多项式求值时可节约大量的乘法计算。对霍纳算法 稻加改进,即可用于求解多项式的不定积分。本题利用积分中值定理估计平均温度即要 求P(x)在[1,6)上的定积分。改进的用于求多项式不定积分的霍纳算法为: function iy=Homer3.n,ac,x)(见代码文件) >>ac=fliplr(c) >>aver=(H er35,ac,0,6)-Horner35,ac,0,1)5 aver=64.5000000000094 (c)由于Ps(x)在=3.5处取得64.5的值,拉格朗日多项式的截断误差为 E65列-B5-35-235-3y05g435-85-o/-p04s28125rmgl 61 如果存在原函数,且原函数的6阶导数有界,那么可由上式求出误差。但是本题中已知的只 有离散的数据点,从图形中可以看出,数据点分布均匀,估计得到的平均值又刚好是数据点 的纵坐标的平均值,所以大致可以认为这个平均值是可靠的
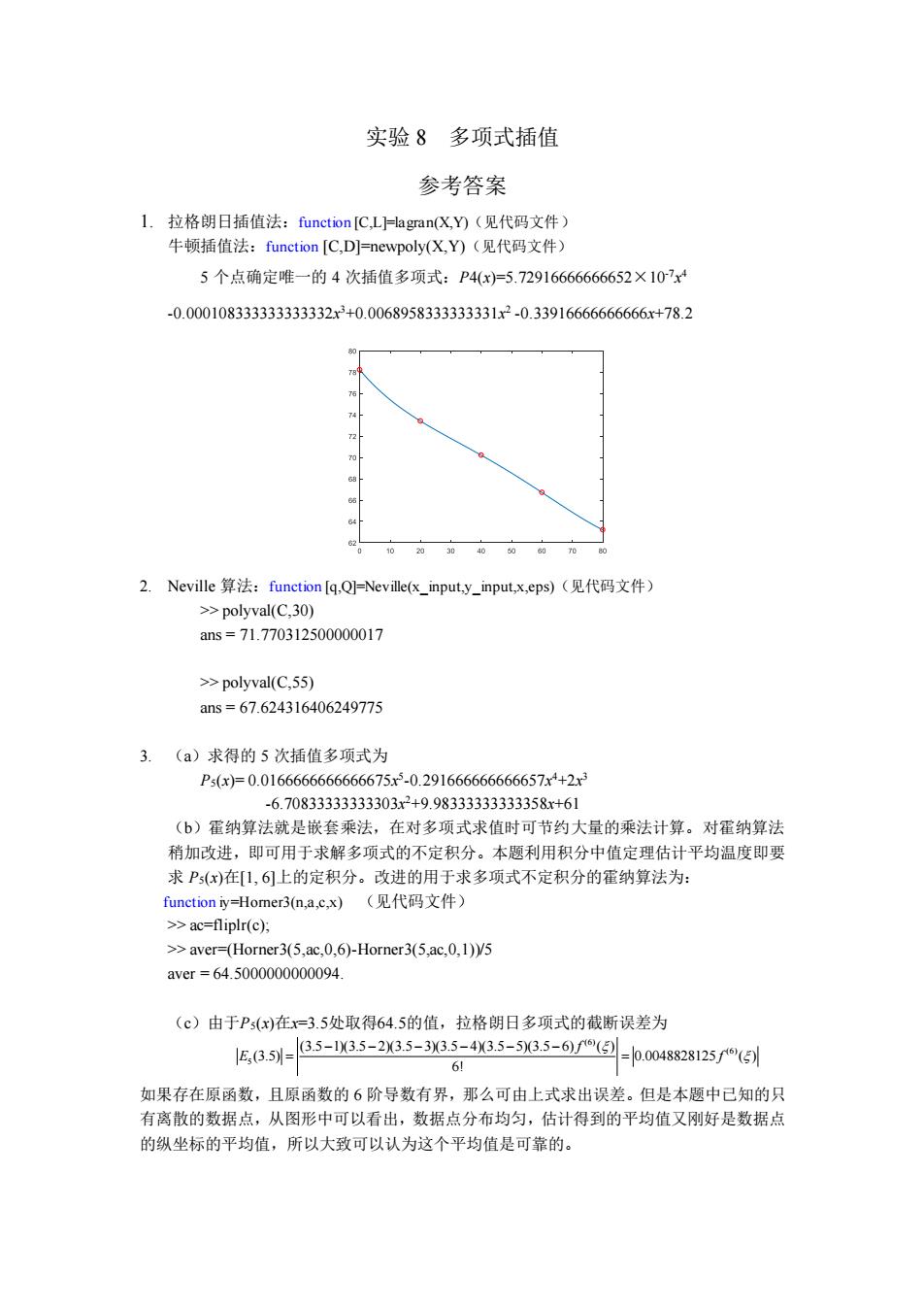
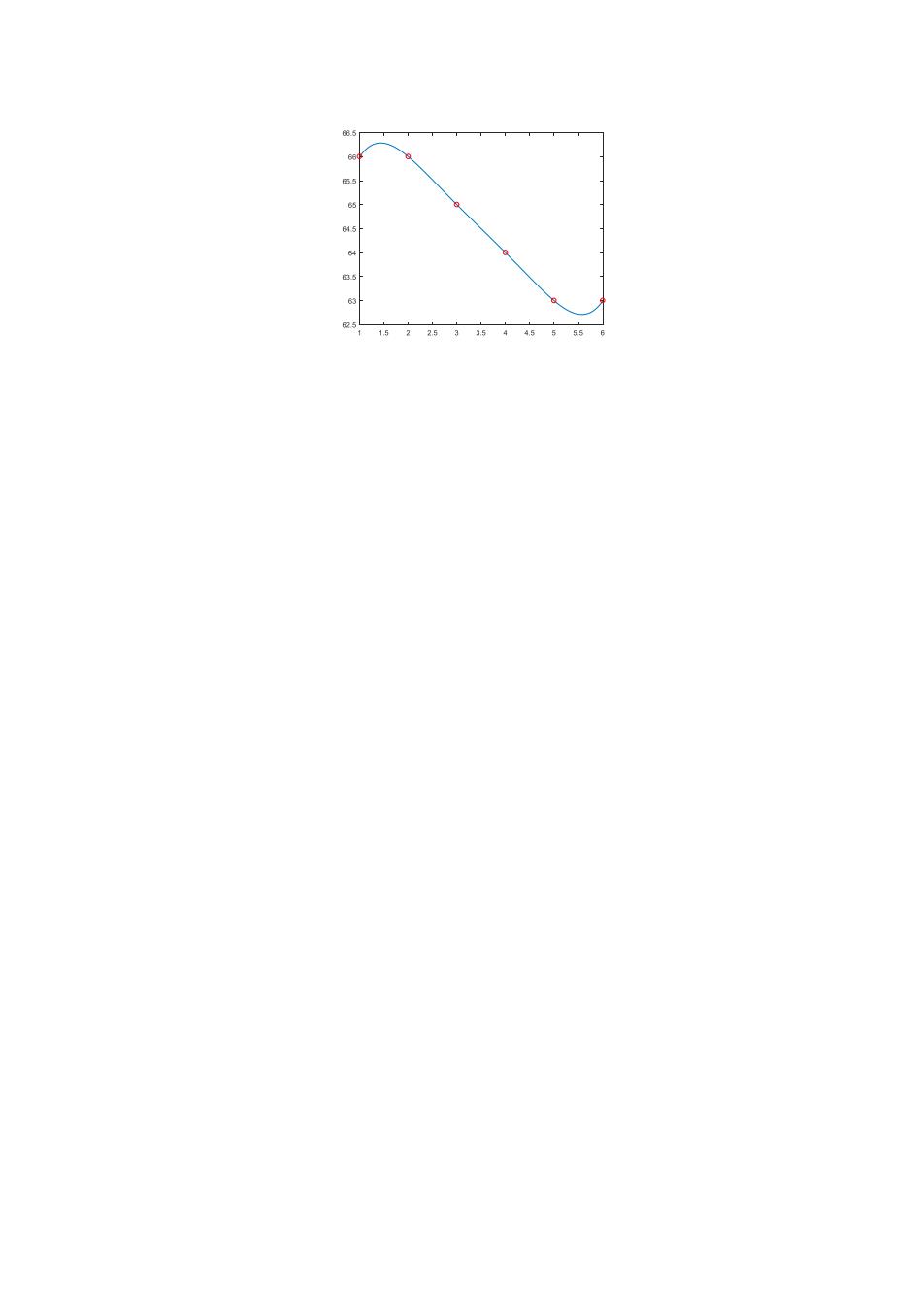
实验 8 多项式插值 参考答案 1. 拉格朗日插值法:function [C,L]=lagran(X,Y)(见代码文件) 牛顿插值法:function [C,D]=newpoly(X,Y)(见代码文件) 5 个点确定唯一的 4 次插值多项式:P4(x)=5.72916666666652×10-7 x 4 -0.000108333333333332x 3+0.0068958333333331x 2 -0.33916666666666x+78.2 2. Neville 算法:function [q,Q]=Neville(x_input,y_input,x,eps)(见代码文件) >> polyval(C,30) ans = 71.770312500000017 >> polyval(C,55) ans = 67.624316406249775 3. (a)求得的 5 次插值多项式为 P5(x)= 0.0166666666666675x 5 -0.291666666666657x 4+2x 3 -6.70833333333303x 2+9.98333333333358x+61 (b)霍纳算法就是嵌套乘法,在对多项式求值时可节约大量的乘法计算。对霍纳算法 稍加改进,即可用于求解多项式的不定积分。本题利用积分中值定理估计平均温度即要 求 P5(x)在[1, 6]上的定积分。改进的用于求多项式不定积分的霍纳算法为: function iy=Horner3(n,a,c,x) (见代码文件) >> ac=fliplr(c); >> aver=(Horner3(5,ac,0,6)-Horner3(5,ac,0,1))/5 aver = 64.5000000000094. (c)由于P5(x)在x=3.5处取得64.5的值,拉格朗日多项式的截断误差为 (6) (6) 5 (3.5 1)(3.5 2)(3.5 3)(3.5 4)(3.5 5)(3.5 6) ( ) (3.5) 0.0048828125 ( ) 6! f E f − − − − − − = = 如果存在原函数,且原函数的 6 阶导数有界,那么可由上式求出误差。但是本题中已知的只 有离散的数据点,从图形中可以看出,数据点分布均匀,估计得到的平均值又刚好是数据点 的纵坐标的平均值,所以大致可以认为这个平均值是可靠的
15729935449559