
1.2.Matrix Multiplication LetA∈Rmxm,B∈RmxP, C=AB∈RmxP, where Cy-∑akbg k=1 Let x,y E R",x'y is the inner product or dot product, xy∈R=xy. i=1 Let x∈Rm,y∈R",xy?is the outer product. X1y1 X1y2 X1yn xy∈Rmxm= X2V1 X2V2 ·x2yn xmy1xm2·Xmyn 10/130
1.2. Matrix Multiplication ▶ Let A ∈ R m×n , B ∈ R n×p , C = AB ∈ R m×p , where Cij = Xn k=1 aikbkj ▶ Let x, y ∈ R n , x Ty is the inner product or dot product, x T y ∈ R = Xn i=1 xiyi . ▶ Let x ∈ R m , y ∈ R n , xyT is the outer product. xyT ∈ R m×n = x1y1 x1y2 · · · x1yn x2y1 x2y2 · · · x2yn . . . . . . . . . . . . xmy1 xmy2 · · · xmyn 10 / 130

Given a matrix A∈Rmxm and a vector x∈R",y=Ax∈Rm.It can be seen from 2 perspectives. 1y is the inner products of the row vectors of A and the column vector x (single vector form) a x y= X= a 对 2 y is the linear combination of the column vectors of 4(multiple column vectors addition form) X1 X2 y=[a1,a2,…,an =a1x1+a2.x2+·+amxn Xn 11/130
▶ Given a matrix A ∈ R m×n and a vector x ∈ R n , y = Ax ∈ R m . It can be seen from 2 perspectives. 1 y is the inner products of the row vectors of A and the column vector x (single vector form) y = a T 1 a T 2 . . . a T m x = a T 1x a T 2x . . . a T mx 2 y is the linear combination of the column vectors of A (multiple column vectors addition form) y = [a1, a2, · · · , an] x1 x2 . . . xn = a1x1 + a2x2 + · · · + anxn. 11 / 130

Similarly,left multiplying row vectors,y=xTA E R",A E Rmx",x E Rm,has 2 ways to see. Inner product of row vector of xand column vectors of 4(single vector form) y=x[a,a2,…,al=[xa,xa2,…,x'an] 2 Linear combination of the row vectors of A (multiple row vectors addition form) a y=1,x2…m =x1a+x2a配+…+xma a 12/130
▶ Similarly, left multiplying row vectors, y T = x TA ∈ R n , A ∈ R m×n , x ∈ R m , has 2 ways to see. 1 Inner product of row vector of x T and column vectors of A (single vector form) y T = x T [a1, a2, · · · , an] = x T a1, x T a2, · · · , x T an 2 Linear combination of the row vectors of A (multiple row vectors addition form) y T = [x1, x2, · · · , xm] a T 1 a T 2 . . . a T m = x1a T 1 + x2a T 2 + · · · + xma T m 12 / 130��
Similarly,C=4B has inner product,outer product,row and column combinations forms. Inner product (single matrix form) a afbi afb2 azbi azb2 azbp C= b1,b2,…,bnl= a ambi ab2…abp 2 Outer product (multi-matrices addition form) b C=[a1,a2,·,an ∑ab好 = b 13/130
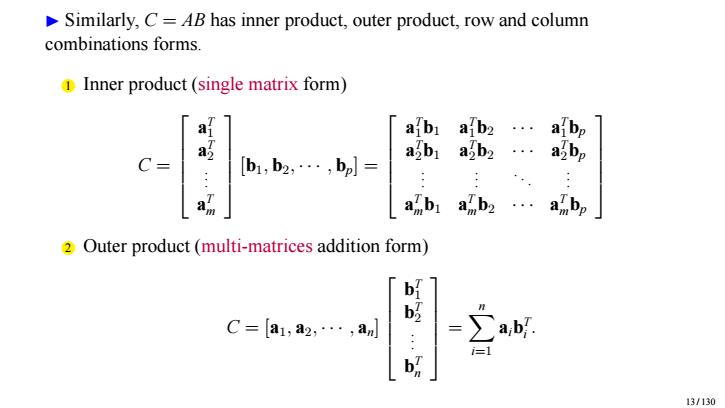
▶ Similarly, C = AB has inner product, outer product, row and column combinations forms. 1 Inner product (single matrix form) C = a T 1 a T 2 . . . a T m [b1, b2, · · · , bp] = a T 1b1 a T 1b2 · · · a T 1bp a T 2b1 a T 2b2 · · · a T 2bp . . . . . . . . . . . . a T mb1 a T mb2 · · · a T mbp 2 Outer product (multi-matrices addition form) C = [a1, a2, · · · , an] b T 1 b T 2 . . . b T n = Xn i=1 aib T i . 13 / 130

3 Right multiply column vector(column combination) C=AB=A[b1,b2,·,bpl=[Ab1,Ab2,…,Abpl 4 Left multiply row vectors (row combination) C=AB= B= a】 Matrix multiplication laws (AB)C A(BC),Associative A(B+C)=AB+AC,Distributive over matrix addition AB BA.Non-commutative 14/130
3 Right multiply column vector (column combination) C = AB = A [b1, b2, · · · , bp] = [Ab1, Ab2, · · · , Abp] 4 Left multiply row vectors (row combination) C = AB = a T 1 a T 2 . . . a T m B = a T 1B a T 2B . . . a T mB Matrix multiplication laws (AB)C = A(BC), Associative A(B + C) = AB + AC, Distributive over matrix addition AB ̸= BA, Non-commutative 14 / 130