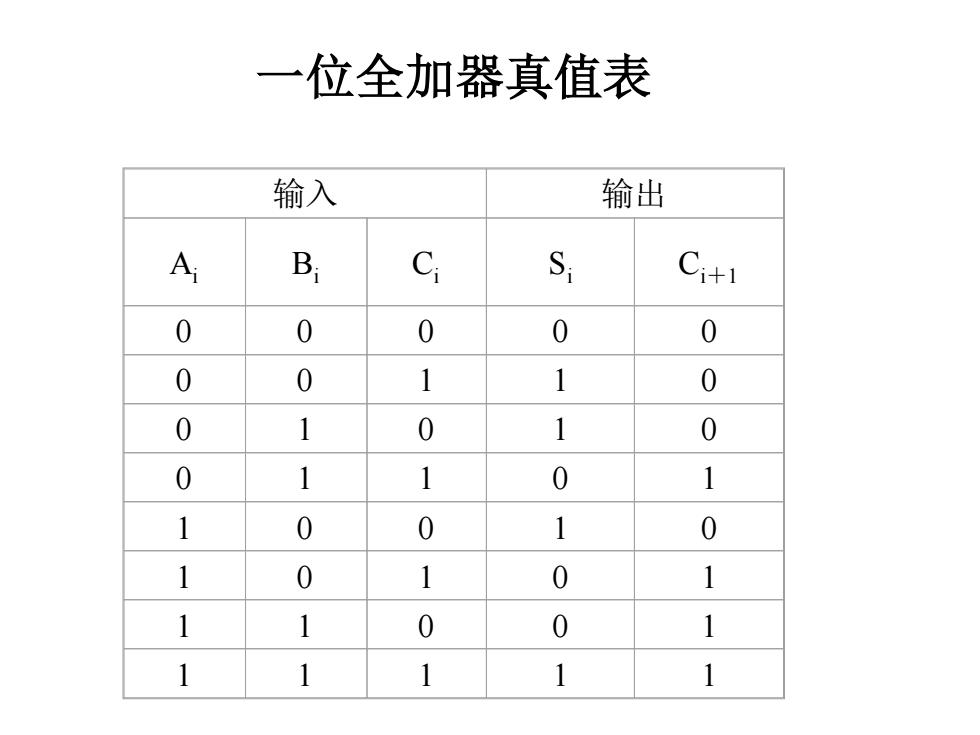
一位全加器真值表 输入 输出 A B C S C+1 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 0 1 0 0 1 1 0 1 0 0 1 1 1 1
一位全加器真值表 输入 输出 Ai Bi Ci Si Ci+1 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1

可按如下逻辑方程进行联系: S=A⊕B田C Ci+1=AB+C(B田A) Ci+1 Si Ci+1 Si FA Bi Ai Ci (a)
可按如下逻辑方程进行联系: Si =Ai⊕Bi⊕Ci Ci+1 =AiBi+Ci (Bi ⊕ Ai ) FA Ci+1 Si Bi Ai Ci
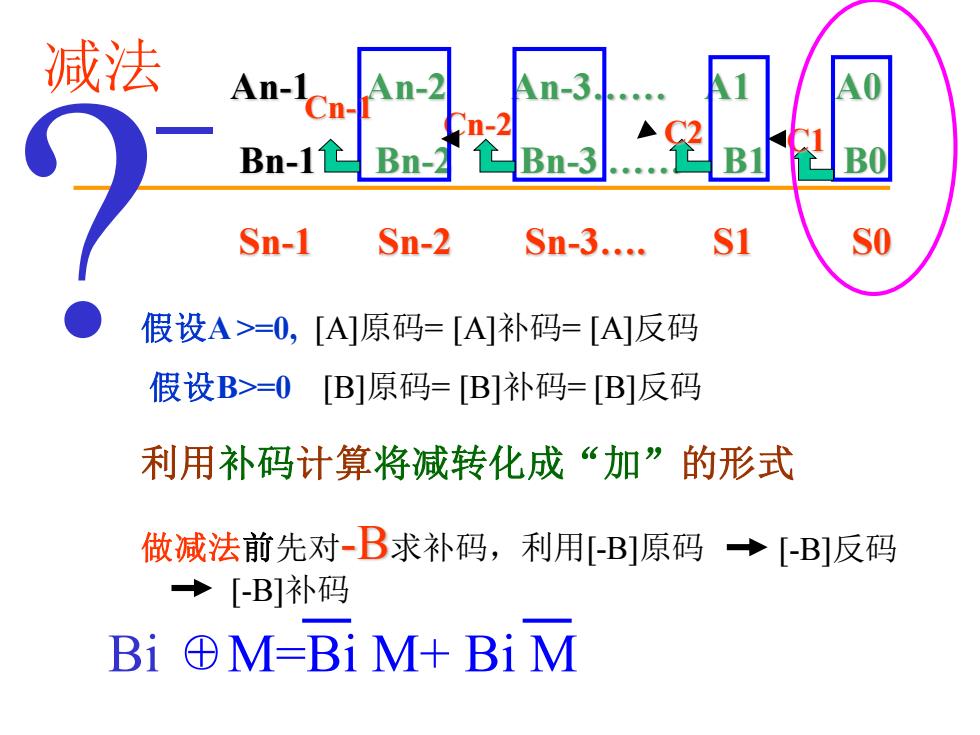
减法 An-1 An-2 3 Cn- Bn-11 Bn-2 Sn-1 Sn-2 Sn-3. S1 SO 假设A>=0,「A]原码=[A]补码=[A反码 假设B>=0[B]原码=B]补码=[B]反码 利用补码计算将减转化成“加”的形式 做减法前先对-B求补码,利用[B]原码→[B]反码 →[-B]补码 Bi⊕M=BiM+BiM
An-1 An-2 An-3. A1 A0 Bn-1 Bn-2 Bn-3 . B1 B0 _ C2 C1 Cn-2 Cn-1 Sn-1 Sn-2 Sn-3. S1 S0 减法 假设A >=0, [A]原码= [A]补码= [A]反码 假设B>=0 [B]原码= [B]补码= [B]反码 Bi ⊕M=Bi M+ Bi M 利用补码计算将减转化成“加”的形式 [-B]反码 [-B]补码 做减法前先对-B求补码,利用[-B]原码
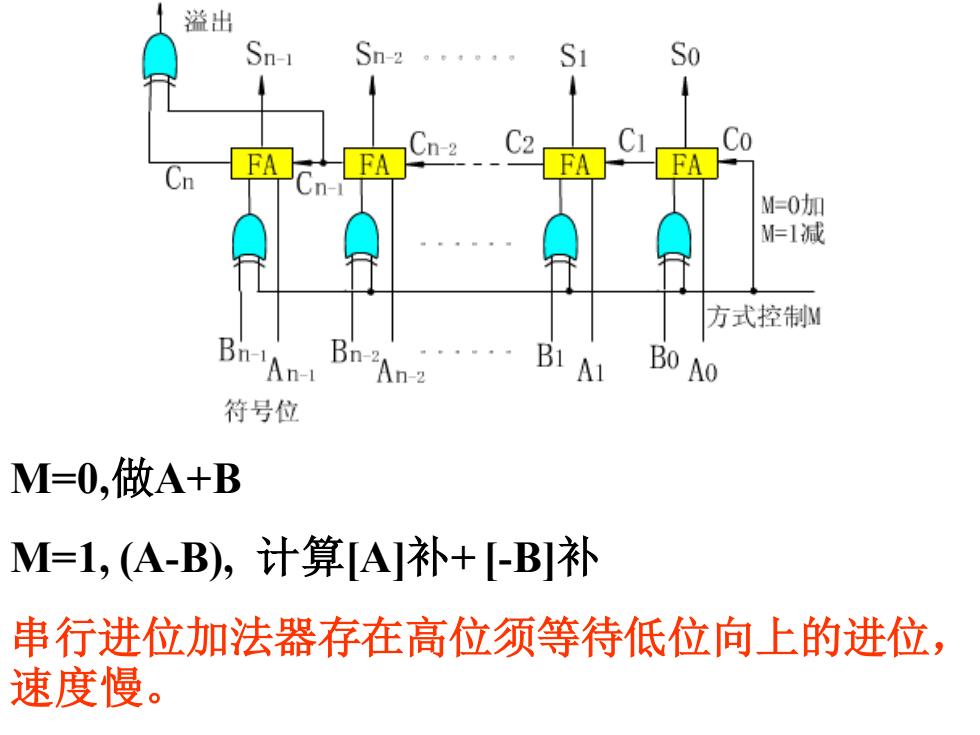
溢出 Sn- Sn- So Co FA FA M=0加 M=1减 方式控制W Bi'An- Bn- An-2 ·B1A1 Bo Ao 符号位 M=0,做A+B M=1,(A-B),计算[A补+[-B]补 串行进位加法器存在高位须等待低位向上的进位, 速度慢
M=0,做A+B M=1, (A-B), 计算[A]补+ [-B]补 串行进位加法器存在高位须等待低位向上的进位, 速度慢
五、十进制加法器(第3版内容,第4版已去掉, 作为课外内容,不考试) 十进制加法器可由BCD码(二一十进制码)来设计 它可以在二进制加法器的基础上加上适当的“校正” 逻辑来实现,该校正逻辑可将二进制的“和”改变 成所要求的十进制格式。 BCD表示中1位十进制数可用4位2进制编码表示 9.1001 8.10007.01116.01105.0101 4.0100 3.00112.00101.00010.0000
五、十进制加法器(第3版内容,第4版已去掉, 作为课外内容,不考试) 十进制加法器可由BCD码(二-十进制码)来设计, 它可以在二进制加法器的基础上加上适当的“校正” 逻辑来实现,该校正逻辑可将二进制的“和”改变 成所要求的十进制格式。 BCD表示中1位十进制数可用4位2进制编码表示 9.1001 8.1000 7.0111 6.0110 5.0101 4.0100 3.0011 2.0010 1.0001 0.0000