[例13-第3版1x=-0.1101,y=一0.1011,求x+y。 解 [x]补=1.0011[]补=1.0101 [X补 1.0011 1.0101 [x十y]补 0.1000 两个负数相加的结果成为正数,这同样是错误的。 两个正数相加,结果大于机器所能表示的最大正数,称为上 溢。而两个负数相加,结果小于机器所能表示的最小负数, 称为下溢。 机器定点数表示 负溢出 正溢出 负小数 正小数 -1 0 +1 负溢出 定点整数表示的范围 正溢出 0 +2
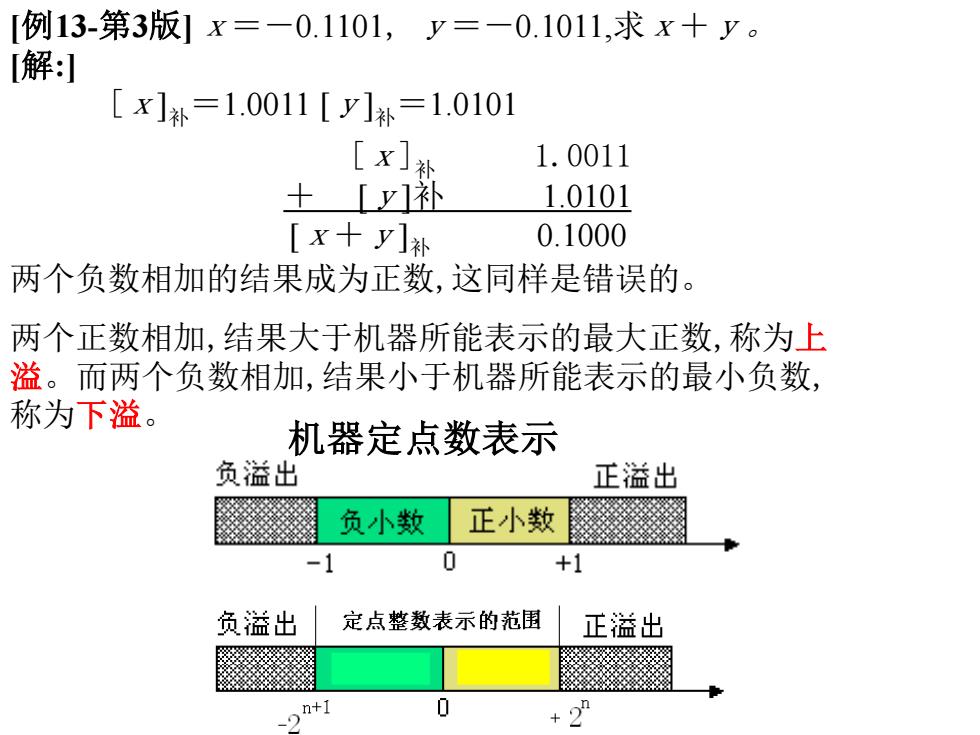
[例13-第3版]x=-0.1101, y=-0.1011,求x+y。 [解:] [x]补=1.0011 [y]补=1.0101 [x]补 1.0011 + [y]补 1.0101 [x+y]补 0.1000 两个负数相加的结果成为正数,这同样是错误的。 两个正数相加,结果大于机器所能表示的最大正数,称为上 溢。而两个负数相加,结果小于机器所能表示的最小负数, 称为下溢。 机器定点数表示

判断溢出的方法(双符号位、单符号位判断方法) 对于小数 第一种方法是采用双符号位法,这称为“变形补码” 或“模4补码”,从而可使模2补码所能表示的数的 范围扩大一倍。变形补码定义为: 2>x≥0 [x]补= 4十x 0>x≥-2 [x]补+[y]补=[x+y]补(mod4)
判断溢出的方法(双符号位、单符号位判断方法) 对于小数 第一种方法是采用双符号位法,这称为“变形补码” 或“模4补码” ,从而可使模2补码所能表示的数的 范围扩大一倍。变形补码定义为: { [x]补= x 2>x≥0 4+x 0>x≥-2 [x]补+[y]补=[x+y]补 (mod 4)

为了得到两数变形补码之和等于两数之和的变形补 码,同样必须: 1.两个符号位都看作数码一样参加运算 2.两数进行以4位模的加法,即最高符号位上产生的 进位要丢掉。 采用变形补码后,如果两个数相加后,其结果的 符号位出现“01”或“10”两种组合时,表示发生溢出。 这是因为两个绝对值小于1的数相加,其结果不会大于 或等于2,所以最高符号位永远表示结果的正确符号
为了得到两数变形补码之和等于两数之和的变形补 码,同样必须: 1. 两个符号位都看作数码一样参加运算 2. 两数进行以4位模的加法,即最高符号位上产生的 进位要丢掉。 采用变形补码后,如果两个数相加后,其结果的 符号位出现“01”或“10”两种组合时,表示发生溢出。 这是因为两个绝对值小于1的数相加,其结果不会大于 或等于2,所以最高符号位永远表示结果的正确符号

对于整数,“变形补码”,可使模2+1补码所能表 示的数的范围扩大一倍。变形补码定义为: [x]补=2n+2+x(m0d2+2) 1)两位符号位均看作数码参加运算2)两数进 行模2+2的加法,从最高符号位上产生的进位 要丢掉。 采用变形码之后,对于任何正数,两个符号位为“0”, 即00xn-1xn-2.x0;对于任何负数,两个符号位为 “1”,即11Xn-1xn-2.x0;若符号位出现“01c10” 为溢出
对于整数,“变形补码”, 可使模2 n+1补码所能表 示的数的范围扩大一倍。变形补码定义为: [x]补 =2n+2+x (mod 2n+2 ) 1)两位符号位均看作数码参加运算 2)两数进 行模2 n+2 的加法,从最高符号位上产生的进位 要丢掉。 采用变形码之后,对于任何正数,两个符号位为“0”, 即00xn-1xn-2.x0;对于任何负数,两个符号位为 “1” ,即11xn-1xn-2.x0 ;若符号位出现“01”“10” 为溢出

[例14-第3版,p34]x=+0.1100,y=+0.1000,求x+y [x]补=00.1100,[]补=00.1000 00.1100 00.1000 01.0100 两个符号位出现“01”,表示已溢出,即结果大于+1
[例14-第3版,p34] x=+0.1100, y=+0.1000,求x+y。 [x]补=00.1100, [y]补=00.1000 + [y]补 00.1000 01.0100 两个符号位出现“01”,表示已溢出,即结果大于+1。 00.1100 [x]补