
电工学↓ 第二节RC电路的暂态过程 零输入响应 零状态响应 电路的全响应 返回
第二节 RC电路的暂态过程 零输入响应 零状态响应 电路的全响应 返回

电工学↓ 一、 零输入响应 如果在换路瞬间储能元件原来就有 能量储存,那么即使电路中并无外施电 源存在,换路后电路中仍将有电压电流 这是因为储能元件要释放能量。 因此,将电路中无输入信号作用时 由电路内部在初始时刻的储能所产生的 响应称为零输入响应。 返回
一、零输入响应 如果在换路瞬间储能元件原来就有 能量储存,那么即使电路中并无外施电 源存在,换路后电路中仍将有电压电流, 这是因为储能元件要释放能量。 因此,将电路中无输入信号作用时, 由电路内部在初始时刻的储能所产生的 响应称为零输入响应。 返回
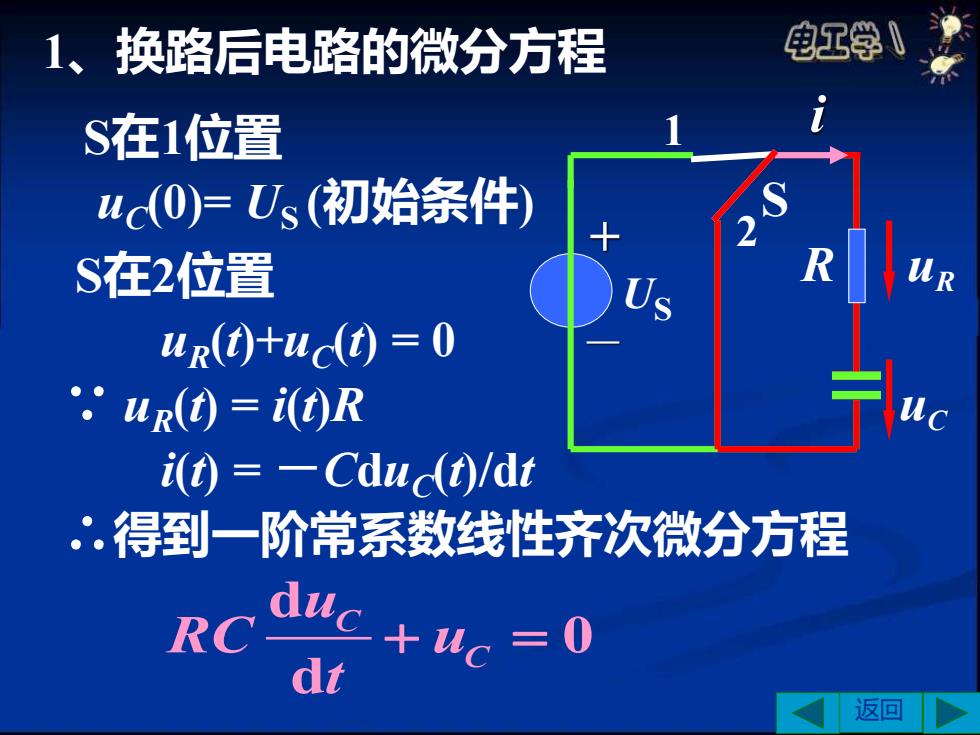
1、换路后电路的微分方程 电工学↓ S在1位置 uc(O)尸Us(初始条件) S在2位置 ur()+uc()=0 ".ur(t)i(t)R i(t)-Cdud(t)/dt ∴.得到一阶常系数线性齐次微分方程 RC duc +uc 0 dt 返回
1、换路后电路的微分方程 S在1位置 uC (0)= US (初始条件) S在2位置 uR (t)+uC (t) = 0 ∵ uR (t) = i(t)R i(t) = -CduC (t)/dt ∴得到一阶常系数线性齐次微分方程 d 0 d C C u RC u t + = + - S i uC R US 1 2 uR 返回

2.解微分方程 电工学↓ RCdud()/dt什uc(t)=0 令它的通解形式为: u=Ae p 代入方程得: (RCP+1)Ae pi=0 .特征方程:RCP+1=0 P=-1/RC ud(t)=Ae -trc uc(0)Us .有A=Us .通解为uc=Use-tRc 返回
2. 解微分方程 RCduC (t) /dt+uC (t) = 0 ∴特征方程 : RCP+1= 0 P =-1/RC uC (t)= Ae-t/RC ∵ uC (0) = US ∴有 A = US ∴通解为 uC (t)=US e -t/RC 令它的通解形式为: uC=Ae pt 代入方程得: (RCP+1) Ae pt = 0 返回

i(t)=C dud(t)/dt 电工学↓ =Cd(Use-uRc)dt =一 (Us/R)e-tRc uR(t)=i(t)R=-Us e-URc 显然uc、uR都是按同样的指数规 律变化的,且都是按指数规律衰减,最 后趋于零。 令RC,称为R、C串联电路的时间 常数,单位s。 返回
显然uC、i、uR都是按同样的指数规 律变化的,且都是按指数规律衰减,最 后趋于零。 i(t)=C duC (t)/dt =C d(USe-t/RC) /dt =-(US /R) e-t/RC uR (t) = i(t) R =-US e-t/RC 令τ=RC,称为R、C串联电路的时间 常数,单位s。 返回