第五章消息认证算法:5.2杂凑函数 5.2.1杂凑函数的定义及使用方式 第三类:带密钥的hash(共享秘密值),实际上是一种MAC ·⑤发方计算消息M和秘密值S链接在一起的杂凑值,作为 M的认证码:见图3(e) 要求通信双方共享一个秘密值S;提供消息的认证性、完整性 ⑥对⑤中的消息认证码再增加单钥加密运算:见图3() 提供消息的保密性、认证性、完整性 比较 H(MIS) (e)是HMAC标准 (e) 的原型 ()的安全性与带 M 保密性的MAC认 比较 证模式相当 EK[MH(MIIS)] H(MS) (d的安全性最强 安毛子代技大学 17/
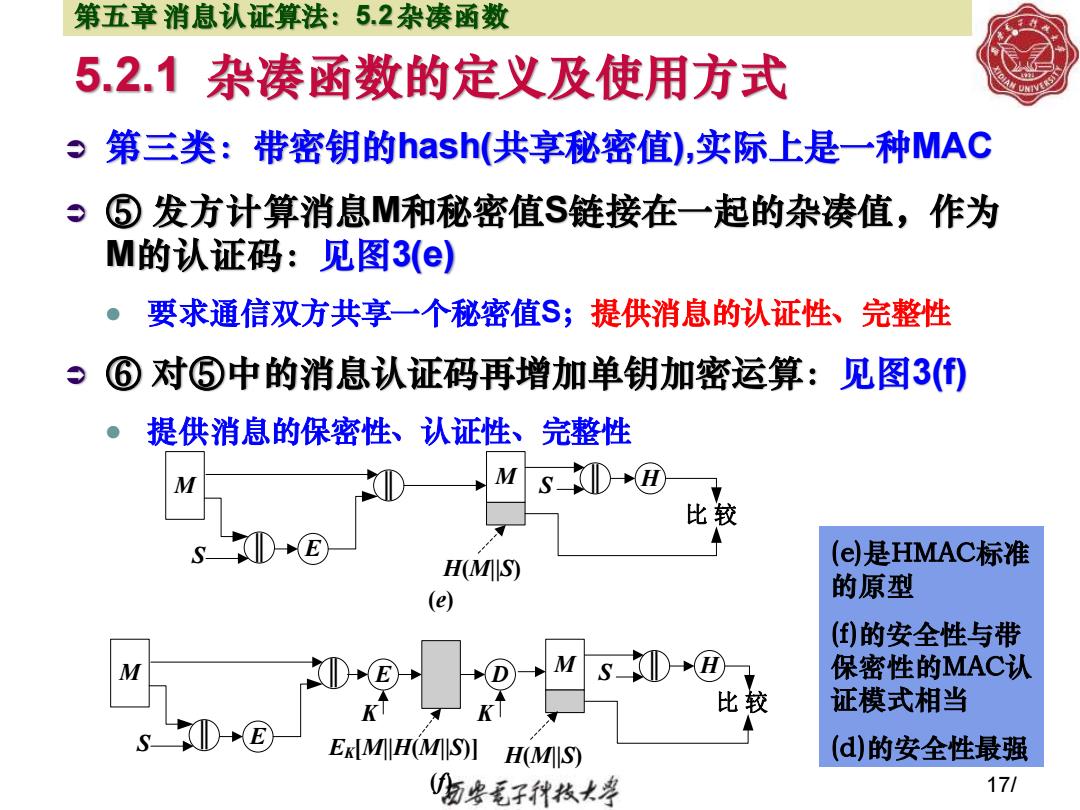
5.2.1 杂凑函数的定义及使用方式 第三类:带密钥的hash(共享秘密值),实际上是一种MAC ⑤ 发方计算消息M和秘密值S链接在一起的杂凑值,作为 M的认证码:见图3(e) ⚫ 要求通信双方共享一个秘密值S;提供消息的认证性、完整性 ⑥ 对⑤中的消息认证码再增加单钥加密运算:见图3(f) ⚫ 提供消息的保密性、认证性、完整性 17/ 第五章 消息认证算法:5.2 杂凑函数 M E ║ M ║ 比 较 (e) H(M||S) S ║ S H M E ║ M ║ 比 较 (f) H(M||S) S ║ E S H K D K EK[M||H(M||S)] (e)是HMAC标准 的原型 (f)的安全性与带 保密性的MAC认 证模式相当 (d)的安全性最强

第五章消息认证算法:5.2杂凑函数 5.2.2杂凑函数应满足的条件 杂凑函数的目的是为需认证的数据产生一个“指纹”。为 了能够实现对数据的认证,杂凑函数应满足以下条件: ①函数的输入可以是任意长 ② 函数的输出是固定长 ③ 已知x,求H(x)较为容易,可用硬件或软件实现 前3个是杂凑函数能用于消息认证的基本要求 ④已知h,求使得Hx)=h的x在计算上是不可行的,这 一性质称为函数的单向性,称H(x)为单向散列函数 。单向性对使用秘密值的认证技术(见图3(e)极为重要。假 如不具有单向性,则攻击者截获M和C=H(S)后,求C的 逆SM,就可求出秘密值S 历粤花子代枝大学 18/
5.2.2 杂凑函数应满足的条件 杂凑函数的目的是为需认证的数据产生一个“指纹”。为 了能够实现对数据的认证,杂凑函数应满足以下条件: ⚫ ① 函数的输入可以是任意长 ⚫ ② 函数的输出是固定长 ⚫ ③ 已知x,求H(x)较为容易,可用硬件或软件实现 ⚫ 前3个是杂凑函数能用于消息认证的基本要求 ⚫ ④ 已知h,求使得H(x)=h的x在计算上是不可行的,这 一性质称为函数的单向性,称H(x)为单向散列函数 ⚫ 单向性对使用秘密值的认证技术(见图3(e))极为重要。假 如不具有单向性,则攻击者截获M和C=H(S‖M)后,求C的 逆S‖M,就可求出秘密值S 18/ 第五章 消息认证算法:5.2 杂凑函数

第五章消息认证算法:5.2杂凑函数 5.2.2杂凑函数应满足的条件 ⑤已知x,找出y0≠x)使得H0y)=Hx)在计算上是不可行的 。满足这一性质的单向散列函数称为弱单向散列函数weekly collision-free ⑥找出任意两个不同的输入xy,使得H0y)=H(x)在计算上是不可行 的 ·如果单向散列函数满足这一性质,则称其为强单向散列函数 strong collision-free ·第⑥个条件用于抵抗生日攻击 ·第⑤和第⑥个条件给出了杂凑函数无碰童性collision-free的概念 9杂凑函数的碰撞collision 设x和y是两个不同的消息,如果Hy)=Hx)则称x和y是杂凑函数的一 个碰撞 历粤毛子代牧大学 19/
5.2.2 杂凑函数应满足的条件 ⚫ ⑤ 已知x,找出y(y≠x)使得H(y)=H(x)在计算上是不可行的 ⚫ 满足这一性质的单向散列函数称为弱单向散列函数weekly collision-free ⚫ ⑥ 找出任意两个不同的输入x、y,使得H(y)=H(x)在计算上是不可行 的 ⚫ 如果单向散列函数满足这一性质,则称其为强单向散列函数 strong collision-free ⚫ 第⑥个条件用于抵抗生日攻击 ⚫ 第⑤和第⑥个条件给出了杂凑函数无碰撞性collision-free的概念 杂凑函数的碰撞collision ⚫ 设x和y是两个不同的消息,如果H(y)=H(x)则称x和y是杂凑函数的一 个碰撞 19/ 第五章 消息认证算法:5.2 杂凑函数

第五章消息认证算法:5.2杂凑函数 5.2.3生日攻击 。1.第类生日攻击,针对弱单向性 已知一散列函数H有个可能输出,H(x)是一特定输出,若对H随机 取k个输入,则至少有一个输入y使得H0)=H()的概率为0.5时,k有 多大?:PHy)=Hx)=0.5的最小的k 称对散列函数H寻找上述y的攻击为第类生日攻击,复杂度O(2m) 9子 第类生日攻击的概率计算 因为H有个可能的输出,所以输入y产生的输出Hy)等于特定输出 Hc)的概率是1/n,不等的概率是1-1/ o y取k个随机值而函数的k个输出中没有一个等于H(x)的概率等于[1 1/k,所以至少有一个等于Hx)的概率为1-1-1/nk 由(1+x)1+kc,其中x<1,可得1-[1-1/m≈1-[1-k/=k/n 若使上述概率等于0.5,则k=n/2 特别地,若H的输出为比特长,即可能的输出个数1=2m,则=2m1 历粤毛子种技大 20/
5.2.3 生日攻击 1. 第I类生日攻击,针对弱单向性 ⚫ 已知一散列函数H有n个可能输出,H(x)是一特定输出,若对H随机 取k个输入,则至少有一个输入y使得H(y)=H(x)的概率为0.5时,k有 多大?:P(H(y)=H(x))=0.5的最小的k ⚫ 称对散列函数H寻找上述y 的攻击为第I类生日攻击,复杂度O(2m-1 ) 第I类生日攻击的概率计算 ⚫ 因为H有n个可能的输出,所以输入y产生的输出H(y)等于特定输出 H(x)的概率是1/n,不等的概率是[1-1/n] ⚫ y取k个随机值而函数的k个输出中没有一个等于H(x)的概率等于[1- 1/n] k,所以至少有一个等于H(x)的概率为1-[1-1/n] k ⚫ 由(1+x) k≈1+kx,其中|x|<<1,可得 1-[1-1/n] k≈1-[1-k/n]=k/n ⚫ 若使上述概率等于0.5,则k=n/2 ⚫ 特别地,若H的输出为m比特长,即可能的输出个数n=2m,则k=2m-1 20/ 第五章 消息认证算法:5.2 杂凑函数

第五章消息认证算法:5.2杂凑函数 5.2.3生日攻击 2.生日悖论 生日悖论是考虑这样一个问题:在个人中至少有两个人的生日相同 的概率大于0.5时,k至少多大? ●k个人中至少有两个取值相同的概率记为P(365,) 若k≤365,P(365,k)=1一A365/365k,其中A365=365!/365-k)排列 生日悖论就是求使得P(365,k)≥0.5的最小k 当k=23时,P365,23)=0.5073,即上述问题只需23人,人数如此之少 若k=100,则P365,100)=0.9999997,即获得如此大的概率 。这是因为在k个人中考虑的是任意两个人的生日是否相同,在23个 人中可能的情况数为C232=253 历粤毛子代牧大学 21/
5.2.3 生日攻击 2. 生日悖论 ⚫ 生日悖论是考虑这样一个问题:在k个人中至少有两个人的生日相同 的概率大于0.5时,k至少多大? ⚫ k个人中至少有两个取值相同的概率记为P(365, k) ⚫ 若k365,P(365, k)=1-Ak 365 /365k , 其中Ak 365=365!/(365-k)!排列 ⚫ 生日悖论就是求使得P(365,k)≥0.5的最小k ⚫ 当k=23时,P(365,23)=0.5073,即上述问题只需23人,人数如此之少 ⚫ 若k=100,则P(365,100)=0.9999997,即获得如此大的概率 ⚫ 这是因为在k个人中考虑的是任意两个人的生日是否相同,在23个 人中可能的情况数为C23 2=253 21/ 第五章 消息认证算法:5.2 杂凑函数