
3.素质要求:具备初步的抽象概括问题的能力.自主学习的能力以及一定的逻辑推理能力。 三、教学内容 第八章空间解析几何与向量代数 1基本内容 向量及其线性运算:空间直角坐标系,向量概念,向量的线性运算,向量的模方向角投 影:数量积,向量积,混合积:平面及其方程:平面的点法式,一般式及其它几种形式,两平 面的夹角:空间直线及其方程:一般方程,对称式方程与参数方程,点线面的关系;曲面及其 方程:曲面方程的概念,旋转曲面,柱面,二次曲面:空间曲线及其方程:一般方程和参数方 程,空间曲线在坐标轴上的投影。 2教学基本要求: 理解空间直角坐标系,向量概念,向量的线性运算,向量的模方向角投影:熟悉掌握数量 积,向量积,混合积的运算:平面方程:空间直线方程。了解曲面方程的概念,旋转曲面,柱 面,二次曲面,掌握投影曲线的求法。 3教学重点难点: 向量的线性运算:数量积,向量积,混合积的运算:空间直线方程的求解。难点为数量积 向量积,混合积的运算:空间直线方程的求解。 4教学建议: 采用讲授法提问法课堂讨论法开展本章课程的学习。 第九章多元函数微分法及其应用 1基本内容: 多元函数的定义,函数概念,区域,二元函数的几何表示,二元函数的极限与连续性,有 界闭区域上连续函数性质的叙述。偏导数的定义,高阶偏导数,混合偏导数可以交换求导次序 的条件(叙述),全微分存在的必要条件和充分条件,全微分在似计算中的应用,多元复合函数 求导法则,隐函数求导公式(一个方程,方程组),方向导数,梯度,二元函数的泰勒公式(叙 述)。空间曲线的切线与法平面,曲面的切平面与法线,多元函数的极值及其求法,条件极值, 拉格朗日乘数法,最大值,最小值问题。 2.教学基本要求: 理解多元函数,偏导数和全微分概念,多元函数的极值概念。熟悉掌握复合函数的求导法。 了解全微分存在的必要条件和充分条件,曲线的切线与法平面及曲面的切平面与法线,条件极 值的概念,方向导数,梯度。掌握计算方向导数,梯度,求曲线的切线和法平面,求曲面的切 15
15 3. 素质要求:具备初步的抽象概括问题的能力.自主学习的能力以及一定的逻辑推理能力。 三、教学内容 第八章 空间解析几何与向量代数 1.基本内容: 向量及其线性运算:空间直角坐标系,向量概念,向量的线性运算,向量的模.方向角.投 影;数量积,向量积,混合积;平面及其方程:平面的点法式,一般式及其它几种形式,两平 面的夹角;空间直线及其方程:一般方程,对称式方程与参数方程,点.线.面的关系;曲面及其 方程:曲面方程的概念,旋转曲面,柱面,二次曲面;空间曲线及其方程:一般方程和参数方 程,空间曲线在坐标轴上的投影。 2.教学基本要求: 理解空间直角坐标系,向量概念,向量的线性运算,向量的模.方向角.投影;熟悉掌握数量 积,向量积,混合积的运算;平面方程;空间直线方程。了解曲面方程的概念,旋转曲面,柱 面,二次曲面,掌握投影曲线的求法。 3.教学重点难点: 向量的线性运算;数量积,向量积,混合积的运算;空间直线方程的求解。难点为数量积, 向量积,混合积的运算;空间直线方程的求解。 4.教学建议: 采用讲授法.提问法.课堂讨论法开展本章课程的学习。 第九章 多元函数微分法及其应用 1.基本内容: 多元函数的定义,函数概念,区域,二元函数的几何表示,二元函数的极限与连续性,有 界闭区域上连续函数性质的叙述。偏导数的定义,高阶偏导数,混合偏导数可以交换求导次序 的条件(叙述),全微分存在的必要条件和充分条件,全微分在似计算中的应用,多元复合函数 求导法则,隐函数求导公式(一个方程,方程组),方向导数,梯度,二元函数的泰勒公式(叙 述)。空间曲线的切线与法平面,曲面的切平面与法线,多元函数的极值及其求法,条件极值, 拉格朗日乘数法,最大值,最小值问题。 2.教学基本要求: 理解多元函数,偏导数和全微分概念,多元函数的极值概念。熟悉掌握复合函数的求导法。 了解全微分存在的必要条件和充分条件,曲线的切线与法平面及曲面的切平面与法线,条件极 值的概念,方向导数,梯度。掌握计算方向导数,梯度,求曲线的切线和法平面,求曲面的切

平面和法线。知道二元函数的极限,连续性概念,有界闭区域上连续函数的性质。会求二阶偏 导数,会求隐函数,(包括由方程组确定的隐函数)的偏导数,会求函数的极值,会用拉格朗日 乘数法求条件极值,会求解一些较简单的最大值,最小值的应用问题。 3教学重点难点 多元函数的概念,偏导数的定义,高阶偏导数混合偏导数方向导数梯度的计算。空间曲 线的切线与法平面,曲面的切平面与法线,多元函数的极值及其求法,条件极值,拉格朗日乘 数法,最大值,最小值问愿。难点为多元函数偏导数的计算:多元函数的极值及其求法。 4.教学建议: 采用讲授法提问法课堂讨论法开展本章课程的学习。 第十章重积分 1基本内容 二重积分的定义性质计算法(包括直角坐标和极坐标),二重积分存在定理的叙述,二重 积分在几何中的应用(体积曲面面积),二重积分在物理学中的应用(质量重心.转动贯量引力 等)。三重积分的定义.性质计算法(直角坐标柱面坐标球面坐标)。三重积分在物理学中的应 用(质量重心转动惯量引力等)。 2.教学基本要求: 理解二重积分,三重积分概念。熟悉擎握二重积分的计算法(直角坐标极坐标),熟悉格 林公式。掌握三重积分的计算法(直角坐标柱面坐标球面坐标),两类曲线积分的计算法。知 道重积分的性质。 3教学重点难点: 二重积分的定义性质计算法:二重积分三重积分的应用。难点为二重积分三重积分的应 用。 4教学建议: 采用讲授法提问法课堂讨论法开展本章课程的学习。 第十一章曲线积分与曲面积分 .基本内容 曲线积分的定义(对弧长及坐标)性质计算法应用(质量功)。曲面积分的定义(对面积 及对坐标),性质计算法应用(质量通量)。各类积分间的关系:格林公式,高撕公式,斯托克 斯公式,平面曲面积分与路径无关的条件。 2教学基本要求: 16
16 平面和法线。知道二元函数的极限,连续性概念,有界闭区域上连续函数的性质。会求二阶偏 导数,会求隐函数,(包括由方程组确定的隐函数)的偏导数,会求函数的极值,会用拉格朗日 乘数法求条件极值,会求解一些较简单的最大值,最小值的应用问题。 3.教学重点难点: 多元函数的概念,偏导数的定义,高阶偏导数.混合偏导数.方向导数.梯度的计算。空间曲 线的切线与法平面,曲面的切平面与法线,多元函数的极值及其求法,条件极值,拉格朗日乘 数法,最大值,最小值问题。难点为多元函数偏导数的计算;多元函数的极值及其求法。 4.教学建议: 采用讲授法.提问法.课堂讨论法开展本章课程的学习。 第十章 重积分 1.基本内容: 二重积分的定义.性质.计算法(包括直角坐标和极坐标).二重积分存在定理的叙述,二重 积分在几何中的应用(体积.曲面面积),二重积分在物理学中的应用(质量.重心.转动贯量.引力 等)。三重积分的定义.性质.计算法(直角坐标.柱面坐标.球面坐标)。三重积分在物理学中的应 用(质量.重心.转动惯量.引力等)。 2.教学基本要求: 理解二重积分,三重积分概念。熟悉掌握二重积分的计算法(直角坐标.极坐标),熟悉格 林公式。掌握三重积分的计算法(直角坐标.柱面坐标.球面坐标),两类曲线积分的计算法。知 道重积分的性质。 3.教学重点难点: 二重积分的定义.性质.计算法;二重积分.三重积分的应用。难点为二重积分.三重积分的应 用。 4.教学建议: 采用讲授法.提问法.课堂讨论法开展本章课程的学习。 第十一章 曲线积分与曲面积分 1.基本内容: 曲线积分的定义(对弧长及坐标).性质.计算法.应用(质量.功)。曲面积分的定义(对面积 及对坐标),性质.计算法.应用(质量.通量)。各类积分间的关系:格林公式,高斯公式,斯托克 斯公式,平面曲面积分与路径无关的条件。 2.教学基本要求:

理解两类曲线积分的性质,两类曲面积分的概念及高斯公式,斯托克斯公式,散度,旋度 概念。会运用平面曲线积分与路径无关的条件,会计算两类曲面积分,能用重积分,线面积分 表达一些几何量与物理量。 3,教学重点难点 曲面积分.曲面积分的计算。 4.教学建议: 采用讲授法提问法课堂讨论法开展本章课程的学习。 第十二章无穷级数 1基本内容: 无穷级数及其收敛与发散定义,无穷级数的基本性质,级数收敛的必要条件,几何级数,P 级数及其收敛性,正项级数的比较审敛法和比值审敛法,交错级数及莱布尼兹定理,绝对收敛 和条件收敛。幂级数概念,阿贝尔定理,幂级数的收敛半径与收敛区间,幕级数的四则运算和 连续性,逐项积分,逐项微分,泰勒级数,函数esix.cosx.Ir(1+x).(1+xP等的幂级数展开 式,幂级数在近似计算中的应用举例,欧拉公式。傅里叶级数的概念,函数展开为傅里叶级数 的充分条件(叙述),奇函数和偶函数的傅里叶级数,函数展开为正弦级数或余弦级数,任意区 间上的付立叶级数。 2教学基本要求: 理解无穷级数收敛,发散及和的概念。熟悉几何级数和P级数的收敛性。熟悉掌握正项级 数的比值审敛法,较简单幂级数的收敛域的求法。了解无穷级数收敛的必要条件,绝对收敛与 条件收敛概念,绝对收敛与收敛的关系。掌握正项级数的比较审敛法,交错级数的莱布尼兹定 理,函数esix.cosx.In(1+x)和(I+x尸的麦克劳林展开式。知道无穷级数的基本性质,幂级 数在其收敛区间内的一些基本性质,函数展开为泰勒级数的充要条件,函数展开为傅里叶级数 的充分条件,函数项级数的收敛域及和函数概念。能用e*.sinx.cosx..ln(1+x)和I+x严的麦克 劳林展式将一些简单的函数展成幂级数,能将定义在(.)和(-1.1)上的函数展开为傅里 叶级数,能将定义在(0.1)上的函数展开为正弦或余弦级数,能估计交错级数的截断误差,会 用幂级数进行一些近似计算。 3教学重点难点: 级数收敛,发散的判断方法:函数展开为泰勒级数的充要条件。难点为无穷级数收敛的判 定方法:函数展开为泰勒级数。 17
17 理解两类曲线积分的性质,两类曲面积分的概念及高斯公式,斯托克斯公式,散度,旋度 概念。会运用平面曲线积分与路径无关的条件,会计算两类曲面积分,能用重积分,线面积分 表达一些几何量与物理量。 3.教学重点难点: 曲面积分.曲面积分的计算。 4.教学建议: 采用讲授法.提问法.课堂讨论法开展本章课程的学习。 第十二章 无穷级数 1.基本内容: 无穷级数及其收敛与发散定义,无穷级数的基本性质,级数收敛的必要条件,几何级数,P 级数及其收敛性,正项级数的比较审敛法和比值审敛法,交错级数及莱布尼兹定理,绝对收敛 和条件收敛。幂级数概念,阿贝尔定理,幂级数的收敛半径与收敛区间,幂级数的四则运算和 连续性,逐项积分,逐项微分,泰勒级数,函数 x e .sinx.cosx. ln(1+x). (1 x ) 等的幂级数展开 式,幂级数在近似计算中的应用举例,欧拉公式。傅里叶级数的概念,函数展开为傅里叶级数 的充分条件(叙述),奇函数和偶函数的傅里叶级数,函数展开为正弦级数或余弦级数,任意区 间上的付立叶级数。 2.教学基本要求: 理解无穷级数收敛,发散及和的概念。熟悉几何级数和 P 级数的收敛性。熟悉掌握正项级 数的比值审敛法,较简单幂级数的收敛域的求法。了解无穷级数收敛的必要条件,绝对收敛与 条件收敛概念,绝对收敛与收敛的关系。掌握正项级数的比较审敛法,交错级数的莱布尼兹定 理,函数 e x .sinx.cosx.ln(1+x)和 (1 x ) 的麦克劳林展开式。知道无穷级数的基本性质,幂级 数在其收敛区间内的一些基本性质,函数展开为泰勒级数的充要条件,函数展开为傅里叶级数 的充分条件,函数项级数的收敛域及和函数概念。能用 e x .sinx.cosx.ln(1+x)和 (1 x ) 的麦克 劳林展式将一些简单的函数展成幂级数,能将定义在(-л.л)和(-l .l )上的函数展开为傅里 叶级数,能将定义在(0. l )上的函数展开为正弦或余弦级数,能估计交错级数的截断误差,会 用幂级数进行一些近似计算。 3.教学重点难点: 级数收敛,发散的判断方法;函数展开为泰勒级数的充要条件。难点为无穷级数收敛的判 定方法;函数展开为泰勒级数
4教学建议:采用讲授法提问法课常讨论法开展本章课程的学习。 四、教学环节与学时分配 序 教学内容 总学 果外辅导/ 号 时讲课实验上机其他 课外实践 注 第八意向量代数 1210 0 第九章 多元函数的微 20 “其 它”主 第十章重积分 16 14 0 0 要方 第十一章曲线积分与 式为 18 曲面积分 4 0 习题 第十二章级数 1614 0 机动(阶段复习备用)60 0 0 6 0 共计 88 70 0018 0 五、教学中应注意的问题 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教 学中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台拓展空间。不仅把数学 课程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点, 选择适宜的教学方法与教学手段,突出重点化解难点,有意识有目的有重点地营造有利于学生 能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验/实践内容 无 七、考核方式 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空选择计 算或解答题,证明等方式,恩目的难易程度要视学生的实际情况而定。· 总评成绩:平时学习过程的考核占30%,理论闭卷考试成绩占70%,其中平时学习过程包 括平时作业(占总成绩的20%),考勤(占总成绩的5%),课堂表现及课后互动(占总成绩的 5%). 八、教材及主要参考书 1.选用教材: 《高等数学》(上下册,第七版)同济大学主编,高等教育出版社,2014年 2,主要参考书: 山《高等数学》吴赣昌等,《数学物理方程》,中国人民大学出版社,2009年。 2]《高等数学》上下册黄立宏等编,复旦大学出版社,2009年 18
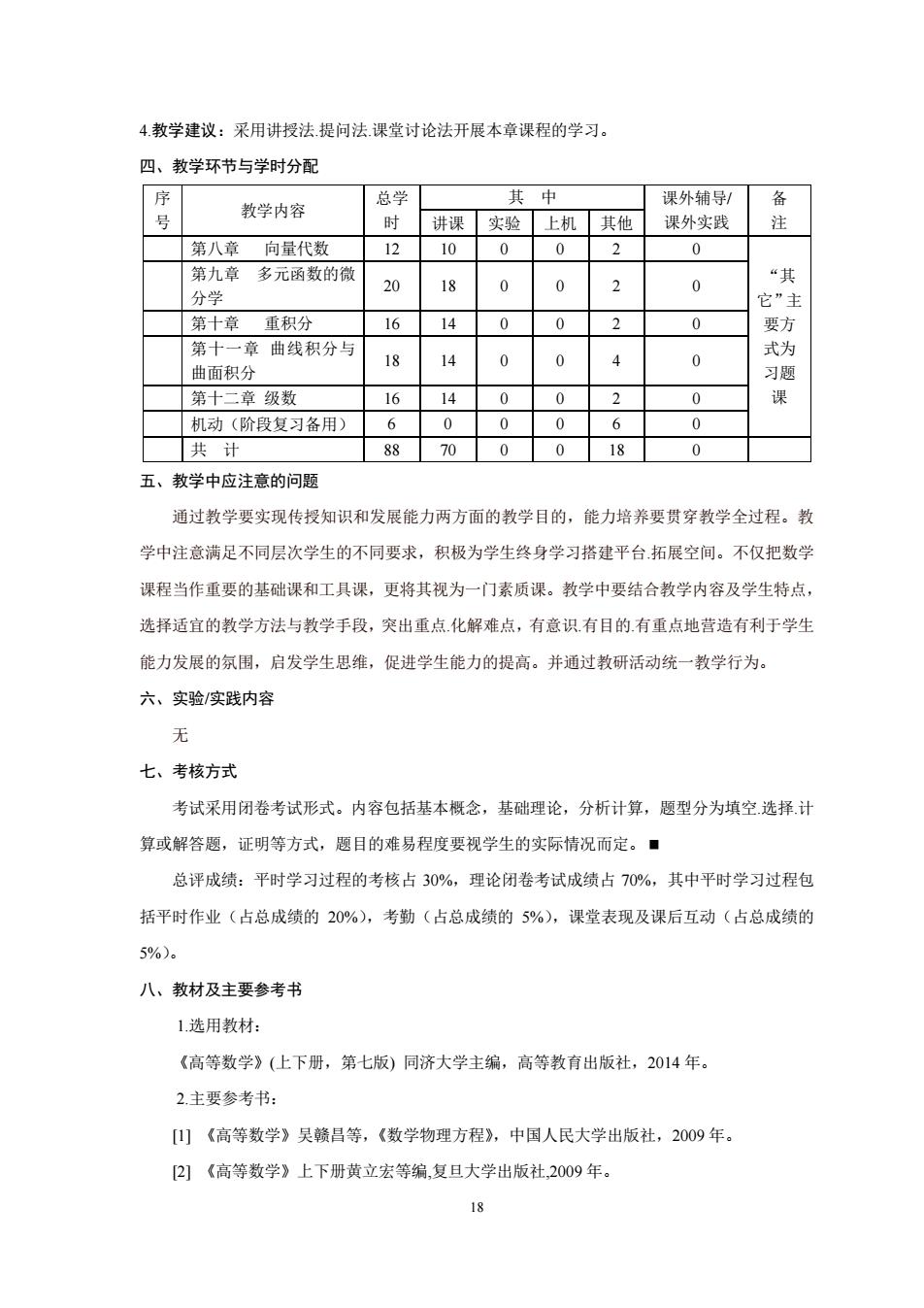
18 4.教学建议:采用讲授法.提问法.课堂讨论法开展本章课程的学习。 四、教学环节与学时分配 序 号 教学内容 总学 时 其 中 课外辅导/ 课外实践 备 讲课 实验 上机 其他 注 第八章 向量代数 12 10 0 0 2 0 “其 它”主 要方 式为 习题 课 第九章 多元函数的微 分学 20 18 0 0 2 0 第十章 重积分 16 14 0 0 2 0 第十一章 曲线积分与 曲面积分 18 14 0 0 4 0 第十二章 级数 16 14 0 0 2 0 机动(阶段复习备用) 6 0 0 0 6 0 共 计 88 70 0 0 18 0 五、教学中应注意的问题 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教 学中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台.拓展空间。不仅把数学 课程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点, 选择适宜的教学方法与教学手段,突出重点.化解难点,有意识.有目的.有重点地营造有利于学生 能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验/实践内容 无 七、考核方式 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空.选择.计 算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 总评成绩:平时学习过程的考核占 30%,理论闭卷考试成绩占 70%,其中平时学习过程包 括平时作业(占总成绩的 20%),考勤(占总成绩的 5%),课堂表现及课后互动(占总成绩的 5%)。 八、教材及主要参考书 1.选用教材: 《高等数学》(上下册,第七版) 同济大学主编,高等教育出版社,2014 年。 2.主要参考书: [1] 《高等数学》吴赣昌等,《数学物理方程》,中国人民大学出版社,2009 年。 [2] 《高等数学》上下册黄立宏等编,复旦大学出版社,2009 年

B)《数学分析》陈纪修,高等教有出版社,2005年。 4《数学复习指南》,陈文灯等编,世界图书出版社,2010年。 九、教改说明及其他 无 执笔人:黄宠辉系室审核人:廖茂新 19
19 [3] 《数学分析》 陈纪修,高等教育出版社,2005 年。 [4] 《数学复习指南》,陈文灯等编,世界图书出版社,2010 年。 九、教改说明及其他 无 执笔人:黄宠辉 系室审核人:廖茂新