吉林大学：《医用物理学》课程电子教案（PPT课件）第三章 振动与波动

四简谐振动的能量 总能量=振子的动能+弹簧的势能 E=Ex+Ep 其中 E.-2k -m-04sin+ cos( -2moA sin'( -kA cos(+) rsnof 心-点

四 简谐振动的能量 总能量=振子的动能+弹簧的势能 E = Ek +E p 2 2 1 E mv k = 2 2 1 E kx p = ( ) 2 m k sin ( ) 注： = 2 1 0 2 2 = k A t + sin ( ) 2 1 0 2 2 2 = m A t +   2 0 sin( ) 2 1 = m −A t + cos ( ) 2 1 0 2 2 = k A t +   2 0 cos( ) 2 1 = k A t + 其中

.Eksin()+cos(o+.) -ksit+)cos(t 系统的动能E随时间周期性变化 系统的势能E,随时间周期性变化 系统的总机械能与时间变化无关，即简谐振动的总能量守恒

cos ( ) 2 1 sin ( ) 2 1 0 2 2 0 2 2 E = k A t + + k A t + 系统的动能 Ek随时间周期性变化 系统的势能 Ep 随时间周期性变化 系统的总机械能与时间变化无关，即简谐振动的总能量守恒 2 2 1 = kAsin ( ) cos ( ) 2 1 0 2 0 2 2 = k A t + + t +

例五 一长度为L的无弹性细线，一端固定在A 人人人∠4人人人∠ 点，另一端悬挂一质量为m、体积很小的 物体。静止时，细线沿竖直方向，物体处 于点O,这是振动系统的平衡位置，如 图。若将物体移离平衡位置，使细线与竖 直方向夹一小角日，然后将物体静止释 放，物体就在平衡位置附近往返摆动起 来。这种装置称为单摆。证明单摆的振动 是简谐振动，并分析其能量 play stop

例五 一长度为L的无弹性细线，一端固定在A 点，另一端悬挂一质 量为m、体积很小的 物体。静止时，细线沿竖直方向，物体处 于点O，这是振动系统的平衡位置，如 图。若将物体移离平衡位置，使细线与竖 直方向夹一小角θ ，然后将物体静止释 放，物体就在平衡位置附近 往返摆动起 来。这种装置称为单摆。证明单摆的振动 是简谐振动，并分析其能量

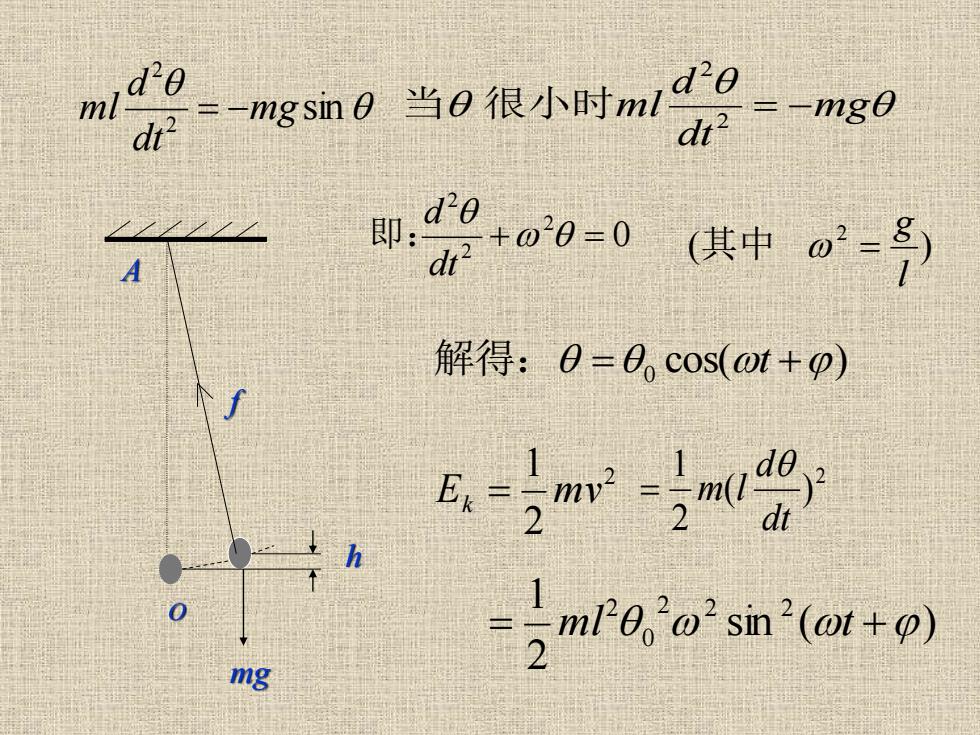
ml di -mgsn0当0很小时nm1 2=-mg 之 A n90-0。-号 解得：0=0cos(ot+p) .2 av y h -nrg,osnam+ol mg

  sin 2 2 mg dt d ml = − cos( ) 解得： = 0 t + 2 2 1 E mv k = h mg f A O 0 2 2 2 +  =  dt d 即：    mg dt d ml = − 2 2 当 很小时 ( ) 2 l g 其中  = sin ( ) 2 1 2 2 2 0 2 = ml   t + 2 ( ) 2 1 dt d m l  =

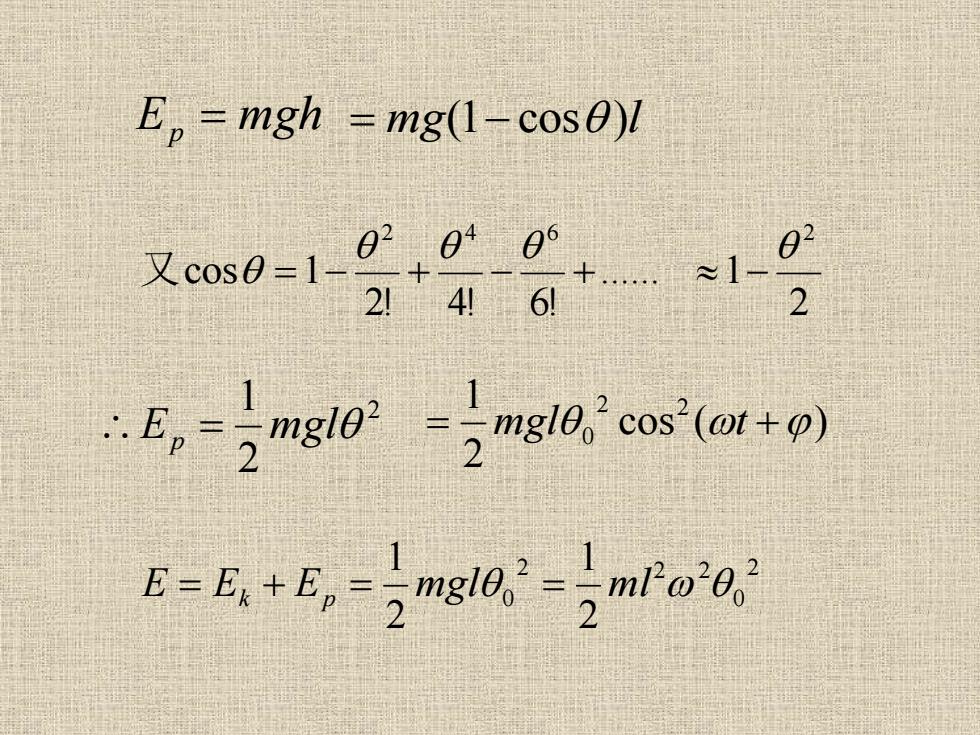
E =mgh =mg(1-cos0)l Xanw-1 t.co() E-E.+E,-]mgl-mF@-O

2 0 2 2 2 0 2 1 2 1 E = Ek + Ep = mgl = m l   2 2 1 Ep = mgl 2 ...... 1 2! 4! 6! cos 1 2 4 6 2     又  = − + − +  − E mgh p = = mg(1− cos )l cos ( ) 2 1 2 2 = mgl 0 t +