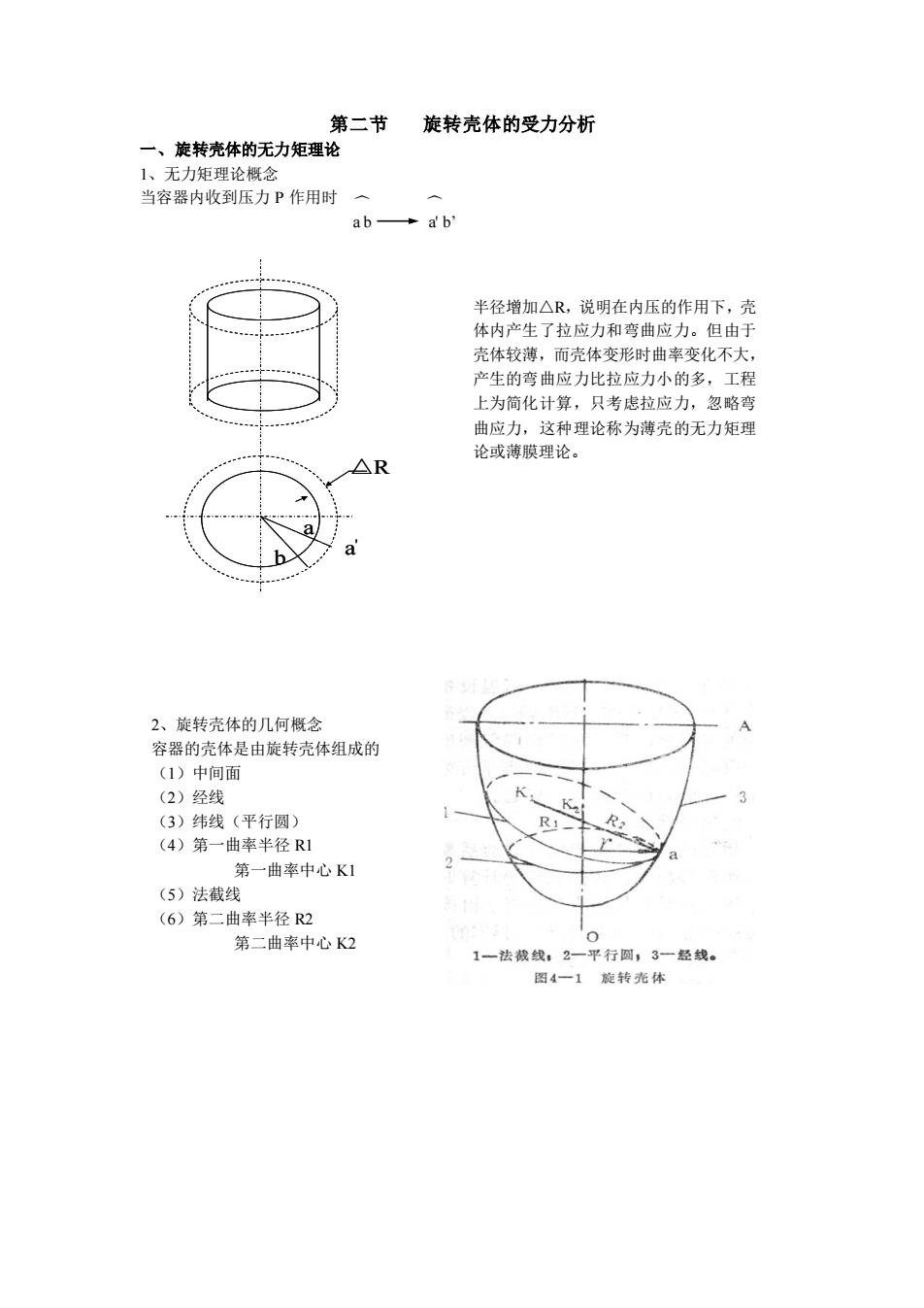
第二节 旋转壳体的受力分析 一、旋转壳体的无力矩理论 1、无力矩理论概念 当容器内收到压力 P 作用时 ︿ ︿ a b a' b’ 半径增加△R,说明在内压的作用下,壳 体内产生了拉应力和弯曲应力。但由于 壳体较薄,而壳体变形时曲率变化不大, 产生的弯曲应力比拉应力小的多,工程 上为简化计算,只考虑拉应力,忽略弯 曲应力,这种理论称为薄壳的无力矩理 论或薄膜理论。 △R a b a ' △R a b a ' 2、旋转壳体的几何概念 容器的壳体是由旋转壳体组成的 (1)中间面 (2)经线 (3)纬线(平行圆) (4)第一曲率半径 R1 第一曲率中心 K1 (5)法截线 (6)第二曲率半径 R2 第二曲率中心 K2
第二节 旋转壳体的受力分析 一、旋转壳体的无力矩理论 1、无力矩理论概念 当容器内收到压力 P 作用时 ︿ ︿ a b a' b’ 半径增加△R,说明在内压的作用下,壳 体内产生了拉应力和弯曲应力。但由于 壳体较薄,而壳体变形时曲率变化不大, 产生的弯曲应力比拉应力小的多,工程 上为简化计算,只考虑拉应力,忽略弯 曲应力,这种理论称为薄壳的无力矩理 论或薄膜理论。 △R a b a ' △R a b a ' 2、旋转壳体的几何概念 容器的壳体是由旋转壳体组成的 (1)中间面 (2)经线 (3)纬线(平行圆) (4)第一曲率半径 R1 第一曲率中心 K1 (5)法截线 (6)第二曲率半径 R2 第二曲率中心 K2
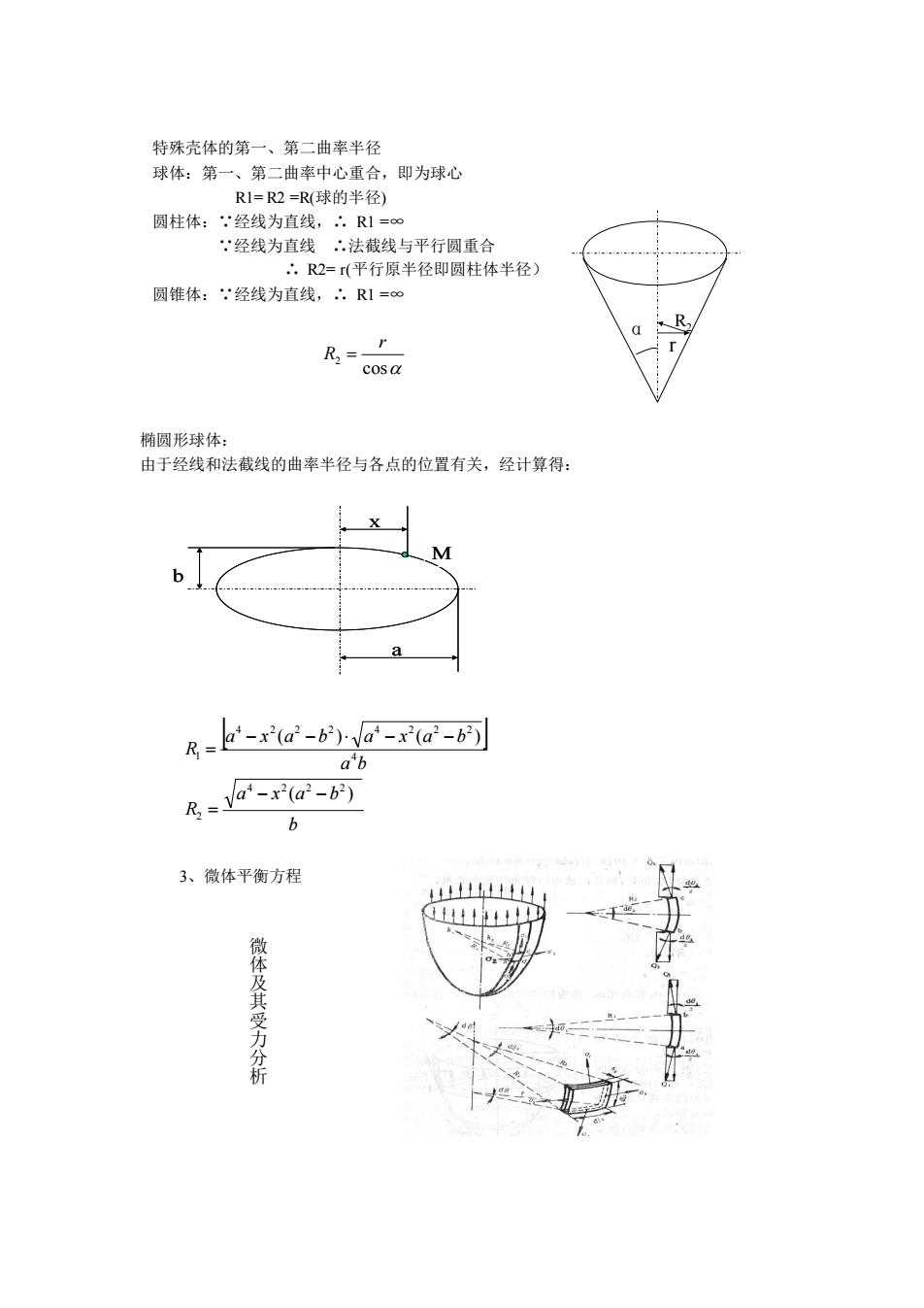
椭圆形球体: 由于经线和法截线的曲率半径与各点的位置有关,经计算得: 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体:第一、第二曲率中心重合,即为球心 R1= R2 =R(球的半径) 圆柱体:∵经线为直线,∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径) 圆锥体:∵经线为直线,∴ R1 =∞ cos 2 r R = R2 r α b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − − − − = a x b M
椭圆形球体: 由于经线和法截线的曲率半径与各点的位置有关,经计算得: 3、微体平衡方程 微 体 及 其 受 力 分 析 特殊壳体的第一、第二曲率半径 球体:第一、第二曲率中心重合,即为球心 R1= R2 =R(球的半径) 圆柱体:∵经线为直线,∴ R1 =∞ ∵经线为直线 ∴法截线与平行圆重合 ∴ R2= r(平行原半径即圆柱体半径) 圆锥体:∵经线为直线,∴ R1 =∞ cos 2 r R = R2 r α b a x a b R a b a x a b a x a b R ( ) ( ) ( ) 4 2 2 2 2 4 4 2 2 2 4 2 2 2 1 − − = − − − − = a x b M

微体上作用的内力和外力见图4一2,图中: 5。—壳体的理论壁厚, 1,一微体沿经线的长度, d12一·体沿法线的长度 R:-一第一曲率半径 R2一一第二曲率半径 d6一一微体上两个第一曲率半径的夹角 d02一微体上两个第二曲率半径的夹角, 1一一经向应力 口2.一环向应力, p 壳体的内压力。 由于内压力的作用,在微体bcd面积(壳体内表面)上所受到的外力。 P=pdl dla 微体四个截面上产生的内力则分别为 bc与ad载面上的径向拉力 Q=dl ab与cd截面上的环向拉力 Q:0:5dl 将微体所受的上述各力,沿微体法线方向投影,得力平衡方程 如5如尊+a如普p 由于微体的曲辛径夹角d0,和d胡,微小故可以作如下近似代换 4量 号是 把它们代入上式,整理后可得: 受量 (-1) 此方程式联系膏膜应力0、:和内压P,称为微体平衡方程式:它由Laplace首先导出, 权称为啦普拉斯方程。

二、无力矩理论的应用
二、无力矩理论的应用

在直径压力相等的情况下,球形壳体的应力只为圆形壳体环向应力的一半,其壁厚也就减 0 0 1 2 2 4S pD S pR = = = =
在直径压力相等的情况下,球形壳体的应力只为圆形壳体环向应力的一半,其壁厚也就减 0 0 1 2 2 4S pD S pR = = = =