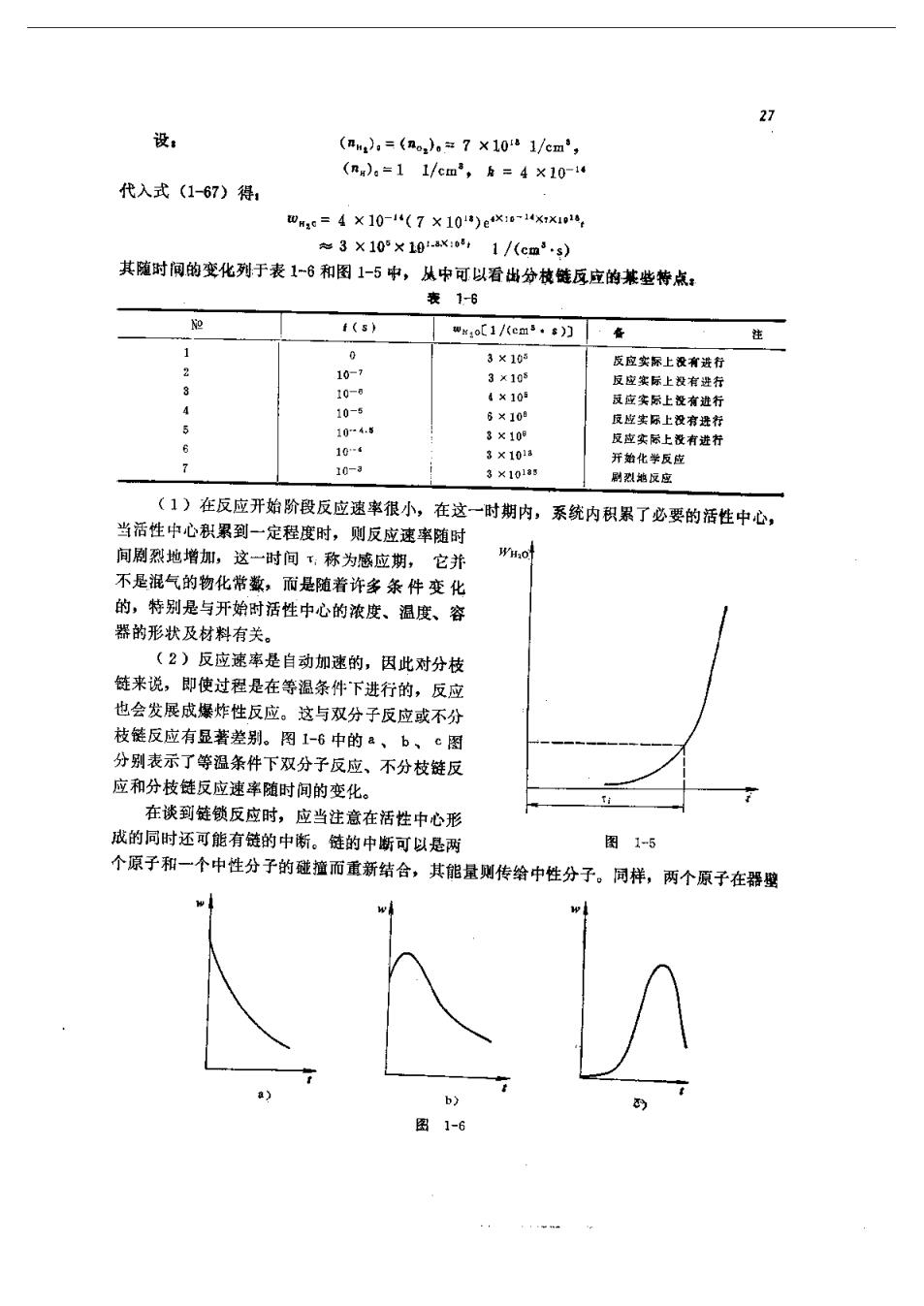
27 设, (m,=(ao=7x101/cm', (n=11/em,k=4x10-1 代入式(1-67)得 四e=4X10-1(7×101)eK14xx1 3×105×10.ax:o,1/(cm3.3) 其随时间的变化列于表1-6和图1-5中,从中可以看出分枝链反应的基些特点: 表16 (5) wm:o[1/(em+s)门·在 0 3×165 3×10 反座瓷层上没有逢行 0- ×10 应实际上没有进 5 104-5 3×101 有进方 3×1010日 刷烈地反宝 (1)在反应开始阶段反应速常很小,在这一时期内,系统内积累了必要的活性中心, 当活性中心积累到一定程度时,则反应速率随时 间剧烈地增加,这一时间,称为感应期, 它并 不是混气的物化带藏,而是随着许多条件变化 的,特别是与开始时活性中心的浓度、温度、容 器的形状及材料有关。 (2)反应速事是自动加速的,因此对分枝 链来说,即使过程是在等温条件下进行的,反应 也会发展成爆炸性反应。这与双分子反应或不分 枝能反应有显著差别。图1-6中的、b、c图 分别表示了等温条件下双分子反应、不分枝链反 应和分枝链反应速率随时间的变化。 在谈到链锁反应时,应当注意在活性中心形 戒的同时还可能有链的中衔。链的中断可以是两 图1-5 个原子和一个中性分子的碰撞而重新结合,其能量则传给中性分子。同样,两个原子在器型

上相碰而结合,把能量传给壁。当反应刚开始时由于活性中心的浓度很小,不易重新缩合, 但当活性中心浓度增加时,究会发生链的中渐。到一定时间时,原子浓度会停业加,这就 会影响反应速率。其次,如果容器内放些能吸收原子的碎玻璃或其他物质,那末容裾中,和 O:的反应速率将大为威低,甚至停止。 从链锁反应的观点出发,前面讲到的某些“反常”现象就可以得到解释。例如带湿下的 冷焰现象武是因为有活性中心在起作用,H0的蒸汽对C0+0:反应的加速作用是由于H,0 在高温下提供了活性中心H和OH的缘故。对于H,和B:的反应,用不分枝链反应来解舞可 以得到与实验结呆相一致的结论。可以采用下列的反应顺序来解释, 链引发(1) 2 Br 链增长(2) Br+H,点HBr+H 能增长(3》H+Br,点,HBr+Br 缝抑制(4)H+HBrH,+B: 链抑制(5)Br+HBr点Ba+H 链终止(6) 2 Br"Brs 链终止(7) 2H鸟H, 研究表明,第(5)步反应和第(7)步反应这两个过程发生的机会很少,因此可以不考意 这时HB肛的反应速率可由上述各反应式联合求得, dGgk.C..Cn+k.CmGa-k.CCe (1-68) 稳定状态的Br原子和H原子的浓度变化是, dC02k.Cm-kC..C +CCu+C.Cm-2kCm (1-69》 C.C-k.C.C..-.C.C (1-70》 由式(1-68)、式(1-69)、式(1-70)联立解得, r好,cc4 (1-71) 孩式与实验得到的结果,即式(1-65)完全一致。 参考文献 C1]A.M.Kansr7,letroduction to Combustion Phene en Gordon and Breach,N.Y.,1975. C2)1.Glassman,Combustion,Academie Press,N.Y.,1977

第2章燃烧物理学基本方程 §2.1引言 研究流体力学,通常采用连续介质力学的观点和方法。所谓连续介质力学,就是说在流 体中取任何一个小领元体或者流体质点,从宏魂上讲,它足够的小,但从徽税上评,它又足 够大,以保证在它的内部仍然还包含有足够多的分子,使其满足热力学量和流体力学量所具 有的宏观统计性质。然烧是气体,液体或固体燃料与氧化剂之间发生的一种猛烈的化学反应, 不管哪一种燃料的燃烧,反应总是全部地,或者部分地在气相中进行,同时,燃烧现象总是 伴有火焰传播和流动,而有的燃烧问题就是在流动系统中发生的。在燃烧死象中,气体是多 组分的,比如有然料气、氧化剂、燃烧产物、情性气、以及各种自由基等。因此,从连续介 质力学角度来看,研究然烧同题,就是研究多组分的带化学反应的流体力学同题 我们这里讲多组分反应流体主要指多组分反应气体。多组分反应流体问愿比经典的流体 力学问题要复杂得多。 因为多组分存在,因此在守恒方程中,还必须增加各个组分的打扩敏方 程;因为有化学反应,因此在扩散方程和能量方程中必须增加物质源项和热源项:当然,气 体的热力学性质、输运性质等也都要依赖于构成系统的组分。 本章对多组分气体的一些基本参盘、输运定律、守恒方程及一些研究问题的方法作一简 单的指述。 §2.2多组分气体基本参量 对于多组分气体,考察一个包围点P(x,y,2)的微元体△Ψ,A少内含有质量△m(:), 那么质点P处的总体质量密度P就是, p()=, A你(t) (2-1) 如果气体中共有N种组分,每一种组分用来表示,那么P点处s组分的质盘密度为: (2-2) 在同一时刻,P点处总体质量密度与每一组分质量密度的关系是 )8) (2-3) 进-步,我们定义(省略掉): 1,=8 (2-4) 称为组分的质量相对浓度,或称为质量百分比浓度

30 由于质量密度与摩尔数间有下列关系: P=CM (2=5) P,=C,M. (2-6》 其中C、C,分别是单位体积中总摩尔数和:组分摩尔数,M和M,分别是混合气的平均分子 量和。组分的分子量。另外,我们还知道,在混合气中,总的摩尔数等于各组分摩尔数之和, c=∑c, (2-7) 因此,电上述的式(23)、式(2-5)、式(2-6)和式(2-7)可以得出多组分气体混合 物的平均分子量是: ∑p,∑c.M, (2-8) 我们再定义: 名=8 (2-9) 称为多组分气体中$组分的摩尔相对浓度,或者说是摩尔百分比浓度。了,和×,间的关系,可 以由式(2-5)和式(2-6)得出: 1=岛 (2-10) 燃烧问题中,一般认为多组分气体服从完全气体定律。由状态方程可以得到: A,=,是,T=C,RT (2-11) P=P是T=CRT (2-12) 将上边两式相除,可以得到关系式, (2-13) 由多组分气体的分压定律,我们知道,气体的总压P等于各组分气体分压中,之和: P=∑P, (2-14) 如果把上边的关系式进一步整理,还可以得到下边几个关系式, M=∑x,M, (2-15) 气=10 (2-16) 2}1 (2-17)

31 M=- 1 (2-18) 如果多组分气体各组分的分子量相差不多或者其中某一组分,的浓度大大大于其他所 有组分的浓变,即当M,M对…sM≈…Mw或者当f,》∑手,时,可以得到下面的 ≠6 简化关系, M≈M. (2-19) (2-20) §2.3分子输运基本定律 分子输运的基本定律是指在不考虑交叉输运现象时,由于速度梯度引起的动量交换定律, 宙于温度梯度引起的热量交换定律;以及由于浓度梯度引起的质量交换定律。也就是牛顿粘 性定律,傅立叶导热定律,以及费克扩散定律。这里仅讨论层流问题,湍流在第6章研究。 §2.3.1牛顿(Newton)粘性定傅 假设有一种等温流体在平面内流动。流速方向为¥方向,垂直于平面定为y方向。如果 流体各层之间流速不同,那么在流速快的一层和流速漫的一层之间就有一个剪切力。流速慢 的一层对流速快的一层有一个阻力。单位面积上剪切力的大小和速度梯度 y戒正比, (2-21) 这公式就称为牛顿粘性定律。*是单位面积上的势切力,:悬动力精性系数(他称为动力黏 度)。是速发梯度,也称剪切速常。负号表示的方向和增加的方向相反。 因为4=,其巾P是流体密度,v是运动粘性系数。因此,当假定P为常数时,牛顿 粘性定律也常写为: au (2-22) 这就得出了剪切力与动量梯度间的关系。 一般来说,气体的粘度与温度的平方根成正比:“。©√T,而液体粘度却浦温度升高而 逐渐威小。 82.3.2傅立叶(Fourier)导热定律 与前边的考虑方式湘类似,假设有一种静止流体,沿著y方向各层之间的湖度不同。那 么由于祖差原因,各层之间就要产生热量交换。热量将从温度较高的一层流向温度较低的一 层。单位时间内、单位面积上的热流是与温度梯度成正比的: (2-23) 这就是傅立叶导热定律。?是单位面积上单位时闻内的热流压,入是导热系数,部是温定 梯度,负号表示热流方询与温度增加的方向相反