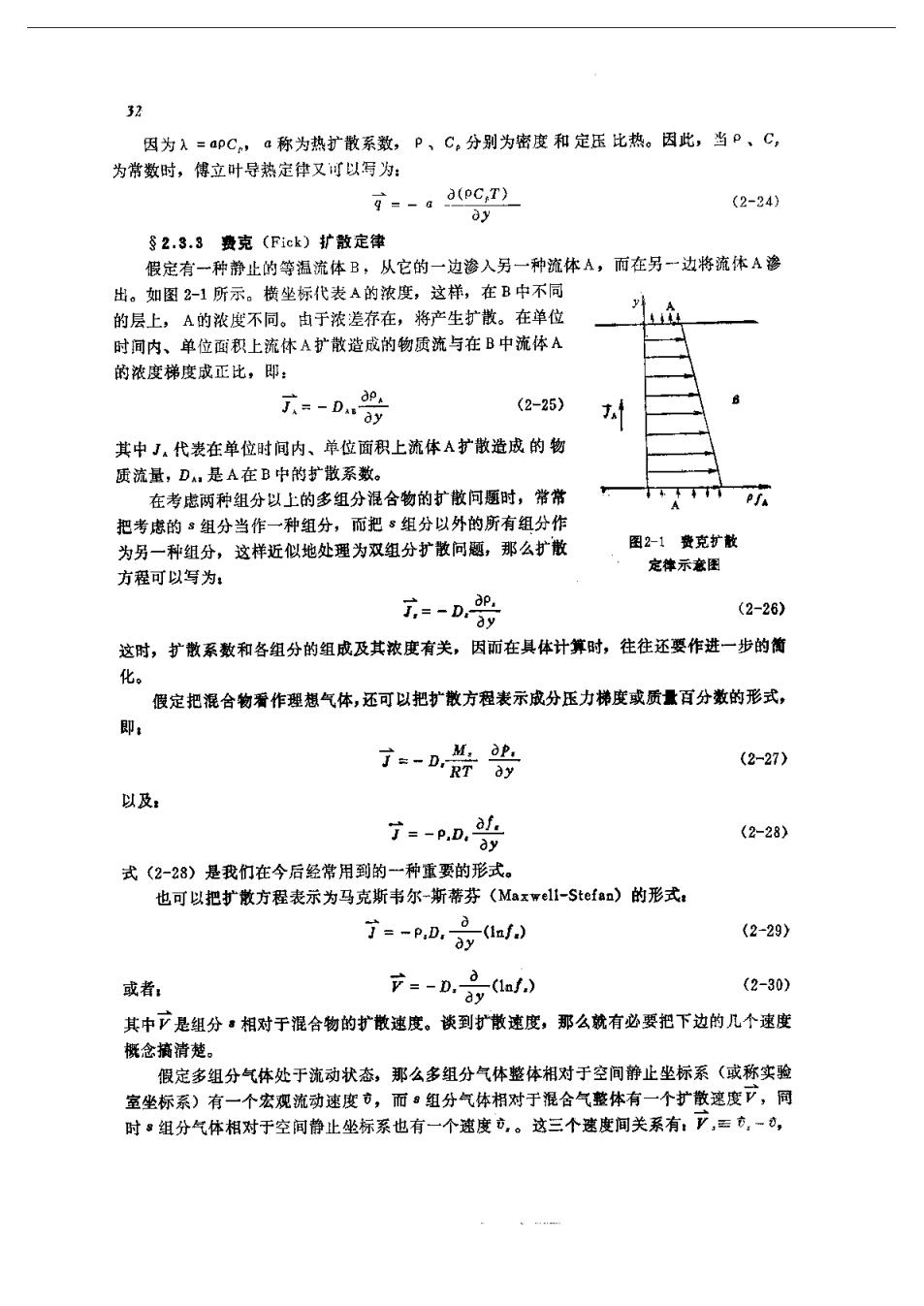
因为入=apC,a称为热扩散系数,P、C,分别为密度和定压比热。因此,当P、G, 为常数时,偶立叶号热定律又可以得为: 7--a (PC,T) (2-24) S2.3.8费克(Fick)扩散定律 假定有一种静止的等海流体B,从它的一边渗入另一种流体A,而在另一边将流体A渗 出。如图2-1所示。樾坐标代表A的浓度,这样,在B中不同 的层上,A的浓度不同。由于浓差存在,将产生扩散。在单位 时间内、单位面积上流体A扩敢造成的物质流与在B中流体A 的浓度梯度成正比,即: -0 (2-25) 其中J,代表在单位时间内、单位面积上流体A扩散造成的物 质流量,D,是A在B中的扩散系数。 在考虑两种组分以上的多组分混合物的扩散问题时,常常 把考虑的组分当作一种组分,而靶组分以外的所有组分作 为另一种组分,这样近似地处理为双组分扩散问题,那么扩散 图21费克扩散 方程可以写为: 定体示意图 (2-26) 这时,扩散系数和各组分的组成及其浓度有关,因而在具体计算时,往往还要作进一步的葡 化。 假定把混合物看作避想气体,还可以把扩散方程表示成分压力梯度或质量百分数的形式, 即 -普韶 (2-27) 以及: 方-AB,的 (2-28) 式(2-28)是我们在今后经常用到的一种重要的形式。 也可以把扩散方程表示为马克斯书尔-斯蒂芬(Maxweli-Stefan)的形式: 寸=-pD,yia时n (2-29) 或者 立-D.}i月 (2-30) 其中立是组分·相对于混合物的扩散速度。谈到扩散速度,那么就有必要把下边的几个速度 概念摘清楚。 假定多组分气体处于流动状态,那么多组分气体鉴体相对于空间静止坐标系(或称实验 室坐标系)有一个宏观流动速度市,而·组分气体相对于混合气整体有一个扩散速度下,同 时组分气体相对于空间静止坐标系也有一个速度,。这三个速度间关系有:产,方,一

33 因此又可以得到,花合气整体相对于静止坐标系的物质流是, 8=pt (2-31) ·组分相对于静止坐标系的物质流是, =p,, (2-32) 组分相对于混合气整体的扩散物质流是: =p,方 (2-33) 同时还应当有关系式: 3,=元,+f.p0 (2-34) 式(2-34)中右增第二项称为混合物整体流所携带的·组分的物质流。 因为混合气整体相对于静止坐标系的物质流就等于各组分相对于静止坐标系物质流分量 之和,即有, 8=∑2, (2-35) 所以又有, 0=21.8, (2-36) 对式(2-3)两边求和,并且利用式(2-31)、式(2-35),可以得到下边重要的关系: 2=∑8-∑0=8-0Σ1.-8-8=0 (2-37) 推导中利用了∑1.=1。式(2-3)说明,在多组分混合物中,通过一个微元表面,各组 分扩散的物质流之和为零!式(2-37)也就是 ∑pP,=0 (2-38) 这就是说,是各组分扩散的物质流矢量和为零而决不是各组分扩散速度的矢盘和为零 (∑≠0). 到此,可以反过来对多组分气体的学热同惠做进一步的描述。多组分气体的导热同题不同 于单组分气体的导热定律所描述的那样,它除了由于温度梯度所造成的热流之外,还应当有 扩散的物质流所携带的给值,即对普通的傅立叶热定律应进行正,而成为修正的傅立叶 导热定律, -+2A (2-39) 其中A,为·组分的给,它应该包括显给和生成(即化学给)两部分,即: hCn (2-40) A,为·组分的生成给,C为组分的定压比热。 罩2.8.4输指系数间的关系 式(2-22),式(2-240和式(2-28),即

F=-v(Pu) 寸-aa“ogn 方=-n0 在形式上是完全一样的。而且,¥、“、D在量细上也完全一样。因此,有时为了简便把它 们写成一种通用形式: (2-41) 只不过在不同的物理量的输运中,F、多、罗所代表的具体物理意义不同要了。 在燃烧现象中,动量输运、能量输运、质量输运常常是同时发生的。因此,带常要讨论 这些输运系数间的关系,这些关系可以组合成下列一些无量纲数: PrEv/a=uC/ (2-42 Se=v/D=W/Dp (2-43) Le=Pr/Sc D/a (2-44) Pr称为普朗特敷(Prandtl Number),Sc称为德密特数(Sehmidt Number)),Le称为路易斯 数(Lewis Number)。 §2.4基本守恒方程 在燃烧物理学中,所谓基本守恒方程是指下面四种守恒方程,即连续牲方程(即憨体质 量守恒方程)、动量守恒方程(即运动方程)、能量守恒方 程、以及扩散方程(即各组分物质守恒方程)。 有的究者 还讨论到各元素的守恒方程,我们这里不作讨论。为丁照质 到各类读者,在本节中对上述四个方程的推导,仅采用直角 坐标系的形式,而一般的通用形式以及在柱坐标和球坐标系 中的表达形式放在本书的附录B中,精读者自已查阅。 §2.4,1连续性方程 △ 考图22所示的一个微元正六面体△xAy△3,流体在 ¥、y、?方向上的分速度分别为:、。、心。假定质景流 困2一2微元正六面体 量、流体密度都是坐标(×,y,)的连续函数。那么,在三个方向的六个面上,我们可 以得到下面一些流量关系, 在&面上流入的质量是: P.4,△y△zAd 在b面上流出的质量是: A“dy△zA,把x方向的P,4△y△z△在¥甲0处技金劳公式展开,并取一阶近似得1 =P.AyAzAt+-(P.)AyAzAxA!

子 因此,在×方向流出的净质量是: m):=D,)△yA2AxA (2-45) 局理在y方向流出的净质量是: (a),=o:,)A2axAyat (2-46) 在z方向流出的净质量是: (△m),= 是R)AAAA (2-47) 把式(2-45),式(2-46)和式(2-47)相加,就得到微元体内流出的净质量为: m-iPy()+(P (2-48) 如果在微元体内没有物质源(或汇),那么流出的净质量就应该等于同一时间内微元体内质量 的变化(在此即为质量的减少),即有等式: 证(p)AxAyAzAI+Am=0 (2-49 把式(2-48)代入到式(2-49)中,且取极限,得到: +)++品-0 (2-50) 对于稳态流动,可简化为: o+多o)+品o)=0 (2-51) 如果把式(2-50)号成向量的形式,即为: P+(p)=0 (2-52) 0 从结果可以看出,多组分气体连续性方程在形式上和单组分气体连续性方程是一样的, 只是要注意这里的密度是多组分气体中各组分密虔的和,即p=工。 824.2动量守恒方程 动量守恒方程,也即是运动方程。它的基确是牛顿运动学第二定律,即徽元体动量的变 化率等于作用在微元体上的外力的矢量和。而作 用于微元体上的力,可以分为两类,一类是体积 力,比如重力、电磁力等,另一类是表面力,比 如压力、粘性力等。 表面力(亦称应力)中的压力是垂直于做元 体的面元素的,而粘性力(亦称剪切力)是与面 元素平行的。由于微元面具有方向,而作用于微 元面上的力也具有方向,它们的方向在一毅情汉 下是不相同的,因面不可能用矢量既表示清楚面 积力的大小和方向,又表示清楚其作用的面元素 的方向。这就要用应力张量来表示,或说是用并 图2-3数元体各面元来上应力分机

36 失来表示。取图?-3所示的微元体,它的各个面上的应力可以表示成图2-3所示的样子 (为了便于表示正方向,我们把图2-2坐标作了转动)。那么作用于微元体所有面元素上应力 的和是 t.ii+ri+r、k (2-53) +下,ki+下kj+t:h板 其中秉是总应力,而:是各个分应力,各项中左边的单位向量是面元素的方向,右边的单 位向量是应力分量的方向。按限连续方程的讨论方法,我们可以得到在×、y、“方向上单 位徽元体所受的净表面力是: -++ (2540 ++ (2-55) 1=g++ (2-56) 而微元体所受体积力分别为, *方向(∑F, y方向(ΣP,)】 (2-57) =方向(空,F), 另一方画,微元体的质量密度是P。在三个方向的加速度分别为: 贤兴+欲+部+“阳 (2-58) 器被+批+"部+“品 (2-59) 肥=+股+v驾+w识 (2-60) 在推导动量方程最终形式时,我们存不加推导地引用粘性流体力学中应力和应变率的如下关 系(这种关系的详细推导请参考精性流体力学方面的教科书): =-p-是(0++8)+2股 -1-(供++股}+2部 -导(股+器±+2“8册 (2-61) w5(号+)