
3.2图像的离散傅立叶变换 o二维离散傅立叶变换(2D-DFT) 1、2D-DFT的定义: W芝2m网g W-1W-1 其中,m,n,u,V都是整数, m=0n=0 N-1N-1 它们的取值范围: F(u,v)W (mum) u=0v=0 0≤m,n,u,v≤N-1 2、几个相关参数: 傅立叶变换表示为复数形式: F(u,v)=R(u,v)+jl(u,v) 上式也可表示成指数形式: F(u,v)=F(u,v)e) 通常称F(u,v)为f(m,n)的频谱或幅度谱,(u,V)为相位。 Fw,)=VR2(u,)+I2(w,) ,(u,v)=arctan I(u,v) R(u,v) 频谱的平方称为功率谱,即: P(u,v)=R2(u,v)+12(u,v) Digital Image Processing
Digital Image Processing Digital Image Processing 3.2 图像的离散傅立叶变换 图像的离散傅立叶变换 ◘二维离散傅立叶变换( 二维离散傅立叶变换(2D-DFT) 1、 2D-DFT的定义: 其中, 都是整数, 它们的取值范围: ⎪⎪⎩ ⎪⎪⎨⎧ = = ∑ ∑ ∑ ∑ − = − = +− − = − = + 1 0 1 0 )( 1 0 1 0 ),( 1 ),( ),( 1 ),( N u N v nvmu N N m N n nvmu N WvuF N nmf Wnmf N vuF ,,, vunm ≤ ≤ Nvunm −1,,,0 2、几个相关参数 、几个相关参数: 傅立叶变换表示为复数形式: 上式也可表示成指数形式: 通常称 为 的频谱或幅度谱, 为相位。 , 频谱的平方称为功率谱,即: = + vujIvuRvuF ),(),(),( ),( ),(),( vuj evuFvuF φ = nmf ),( φ vu ),( ),(),(),( 2 2 = + vuIvuRvuF ),( ),( arctan),( vuR vuI φ vu = ),(),(),( 2 2 = + vuIvuRvuP vuF ),(
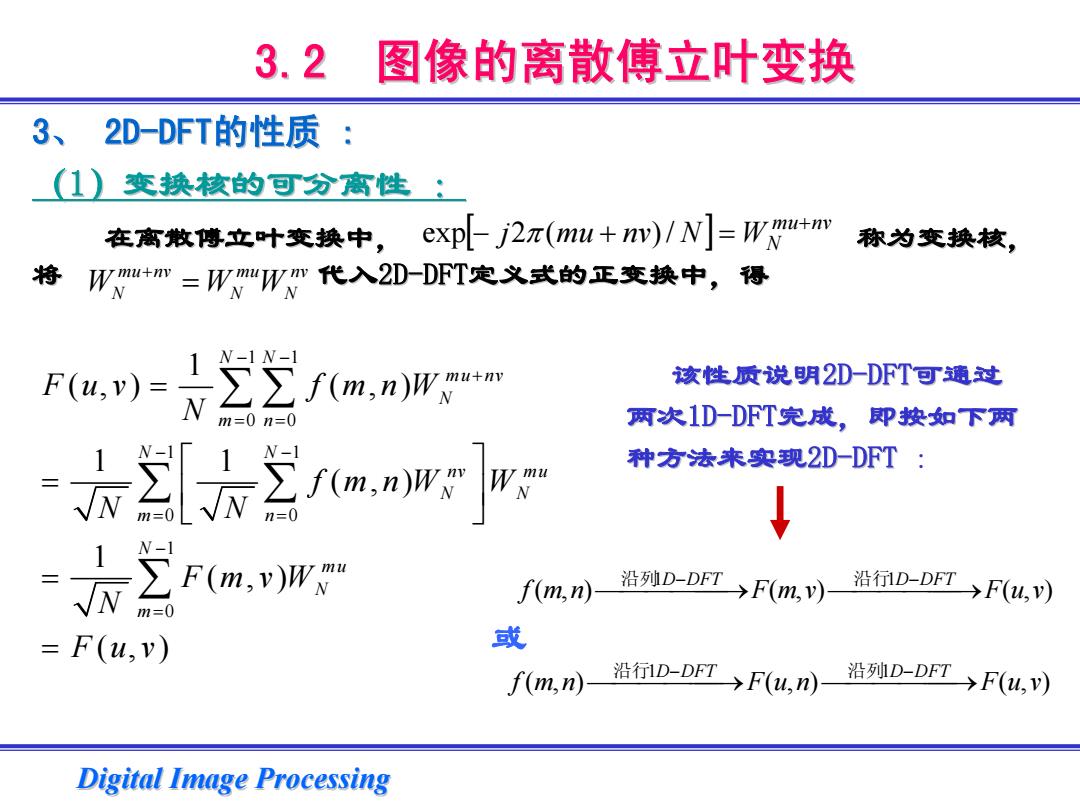
3.2 图像的离散傅立叶变换 3、2D-DFT的性质 (1)变换核的可分离性: 在离散傅立叶变换中, expj2π(u+w)/N]=W+m 称为变换核, 将 WWm+m=WW"WW代入2D-DFT定义式的正变换中,得 Fu-2艺/m源 该性质说明2D-DFT可通过 m=0n=0 两次1D-DFT完成,即按如下两 女[三an 种方法来实现2D-DFT: 芝Fmr W-1 fL小沿n-D7FOm)沿D-FT)Fu,) n0 F(u,v) 或 f(m,n 沿行1D-DFT→F(u,n) 沿列D-DFT→F(u,V) Digital Image Processing
Digital Image Processing Digital Image Processing 3.2 图像的离散傅立叶变换 图像的离散傅立叶变换 3、 2D-DFT的性质 : (1)变换核的可分离性 )变换核的可分离性 : 在离散傅立叶变换中, 称为变换核, 将 代入2D-DFT定义式的正变换中,得 [ ] nvmu WNnvmuj N + π /)(2exp =+− mu nv mu nv W WW N NN + = 1 1 0 0 1 1 0 0 1 0 1 (,) ( , ) 1 1 ( ,) 1 ( ,) (,) N N mu nv N m n N N nv mu N N m n N mu N m F uv f mnW N f mnW W N N F mvW N F uv − − + = = − − = = − = = ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ = = ∑ ∑ ∑ ∑ ∑ 该性质说明2D-DFT可通过 两次1D-DFT完成,即按如下两 种方法来实现2D-DFT : ),( ),( ),( 1 1 nmf vmF vuF ⎯⎯ → 沿列 −DFTD ⎯⎯⎯⎯ ⎯⎯ → 沿行 −DFTD ⎯⎯⎯⎯ ),( ),( ),( 1 1 nmf nuF vuF ⎯⎯ → 沿行 −DFTD ⎯⎯⎯⎯ ⎯⎯ → 沿列 −DFTD ⎯⎯⎯⎯ 或