
3.1.2 信道参数 3.平均条件互信息 设三个离散概率空间K,y,Z,x∈X,y∈y,z∈Z,且有概率关系式 2ΣΣo)=1 (3-10) p(y)=∑p(a)x∈X,y∈Y p(xz)=∑p2) x∈X,z∈Z (3-11) pa)=∑pa)yeY,aez px)=∑p)=∑p) xeX (3-12) py)=∑py)=∑p0a) y∈Y pa)=∑p(y=∑p0a) z∈Z 16
16 3.1.2 信道参数 3.平均条件互信息 设三个离散概率空间X,Y,Z, x X , y Y , z Z ,且有概率关系式 ( ) 1 X Y Z p xyz = ( ) ( ) , ( ) ( ) , ( ) ( ) , Z Y X p xy p xyz x X y Y p xz p xyz x X z Z p yz p xyz y Y z Z = = = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Y Z X Z X Y p x p xy p xz x X p y p xy p yz y Y p z p xy p yz z Z = = = = = = (3-10) (3-11) (3-12)
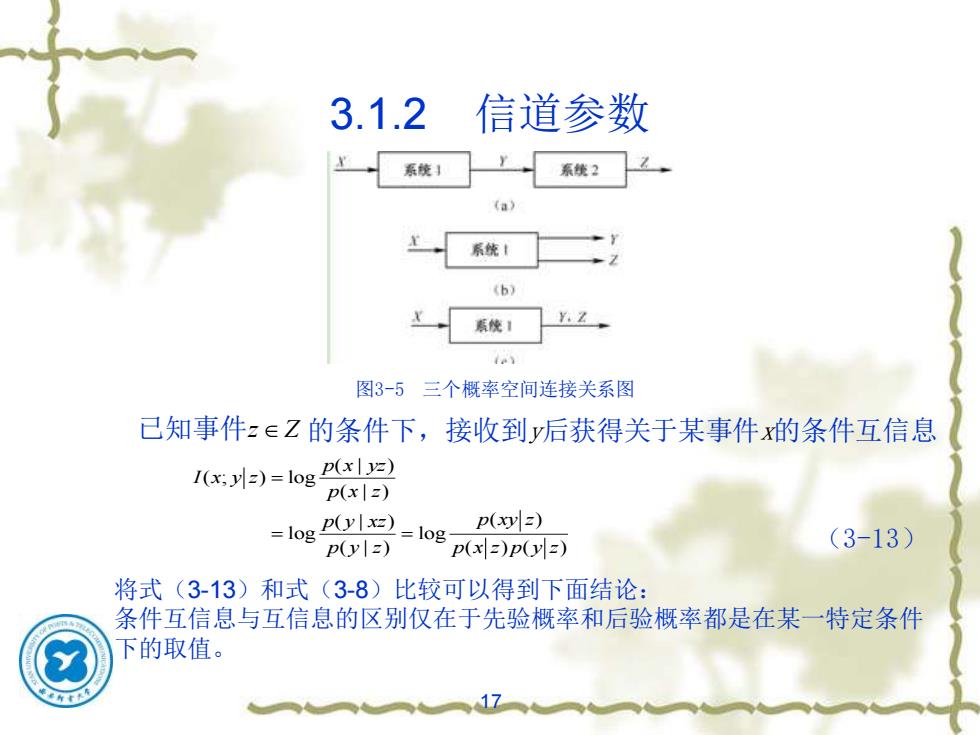
3.1.2 信道参数 系统1 系统2 (a) 系统1 (b) 焉饶1 Y.Z 图3-5三个概率空间连接关系图 已知事件z∈Z的条件下,接收到y后获得关于某事件x的条件互信息 1(x:=)=log p(xly=) p(x=) =log p(yx=) p(xy=) p(yl=) p(x=)p(y=) (3-13) 将式(3-13)和式(3-8)比较可以得到下面结论: 条件互信息与互信息的区别仅在于先验概率和后验概率都是在某一特定条件 下的取值
17 3.1.2 信道参数 图3-5 三个概率空间连接关系图 ( | ) ( ; ) log ( | ) ( | ) ( ) log log ( | ) ( ) ( ) p x yz I x y z p x z p y xz p xy z p y z p x z p y z = = = (3-13) 已知事件 z Z 的条件下,接收到y后获得关于某事件x的条件互信息 将式(3-13)和式(3-8)比较可以得到下面结论: 条件互信息与互信息的区别仅在于先验概率和后验概率都是在某一特定条件 下的取值

3.1.2 信道参数 已知yeY,z∈Z后,x∈X总共获得关于的互信息,即 )=log p(=log (p()-log(+log ( p(x) p(x)p(xly) p(x) p(xly) =1(x,y)+1(x;zy) (3-14) 此关系式表明,yz联合给出关于x的互信息量等于给出关于x的互信 息量与y已知条件下给出关于x的互信息量之和。 I(x;y)=1(x;2)+1(xy) (3-15) xyZ=E[xypj-∑∑∑p()og p(xz) =H(XZ)-H(X ZY) =22∑pe)og p(xyl=) =HXZ)+H(YIZ)-H(XYZ) (3-16) 而平均互信息为 10,Z=Es=∑∑∑)iog p(x) (3-17) 18
18 3.1.2 信道参数 已知 , 后, 总共获得关于的互信息,即 ( | ) ( ; ) log ( ) p x yz I x yz p x = ( | ) ( | ) ( | ) ( | ) log log log ( ) ( | ) ( ) ( | ) p x y p x yz p x y p x yz p x p x y p x p x y = = + = + I x y I x z y ( ; ) ( ; | ) (3-14) y Y z Z x X 此关系式表明,yz联合给出关于x的互信息量等于y给出关于x的互信 息量与y已知条件下z给出关于x的互信息量之和。 I x yz I x z I x y z ( ; ) ( ; ) ( ; | ) = + (3-15) ( | ) ( ; ) ( ; ) ( )log X Y Z ( | ) p x yz I X Y Z E I x y z p xyz p x z = = = − H X Z H X ZY ( | ) ( | ) ( | ) ( )log X Y Z ( | ) ( | ) p xy z p xyz p x z p y z = = + − H X Z H Y Z H XY Z ( | ) ( | ) ( | ) ( ) ( ; ) ( ; ) ( )log X Y Z ( ) p x yz I X YZ E I x yz p xyz p x = = (3-16) 而平均互信息为 (3-17)

3.1.2 信道参数 I(X:YZ)=I(X;Y)+I(X;ZY)=I(X;Z)+I(X;Y Z) (3-18) 平均互信息(X,YZ)是随机变量与联合变量Z之间统计依赖程度的信息测度 例3-1设信源 通过一干扰信道,接收符号 为y=[b%,],信道传递概率如图3-6所示。 求:(1)信源中事件x,和x2分别含有的自信息。 (2)收到消息y,(广1,2)后,获得的关于x (=1,2)的信 息量。 56 (3)信源和信源的信息熵。 16 (4)信道疑义度H(XY)和H(Y|X)噪声熵。 (5)接收到信息后获得的平均互信息。 图3-6二元信道传递概率
19 3.1.2 信道参数 I X YZ I X Y I X Z Y ( ; ) ( ; ) ( ; ) = + = + I X Z I X Y Z ( ; ) ( ; ) (3-18) 平均互信息 I X YZ ( ; ) 是随机变量X与联合变量YZ之间统计依赖程度的信息测度。 例3-1 设信源 通过一干扰信道,接收符号 为 ,信道传递概率如图3-6所示。 求:(1)信源X中事件 和 分别含有的自信息。 (2)收到消息 (j=1, 2)后,获得的关于 (i=1,2)的信 息量。 (3)信源X和信源Y的信息熵。 (4)信道疑义度 和 噪声熵。 (5)接收到信息Y后获得的平均互信息。 1 2 ( ) 0.6 0.4 X x x p x = 1 2 y y y = [ , ] 1 x 2 x j y i x H X Y ( | ) H Y X ( | ) 图3-6 二元信道传递概率

3.1.2 信道参数 解:(1)信源 [6 事件X1含有的自信息为1(x)=-logp(x2)=-log20.6≈0.737bit 事件x2含有的自信息为I(x2)=-logp(x2)=-log20.4≈1.32bit (2)根据题意是计算 1(xy=1,2;产1,2 P1x=gP0,1)-6)=1)4 I(x;y)=log- ly2)=1og p(y;x) p(y,) j=1,2;=1,2 p(x;) py,)=∑(x)p(Y,|x) 户1,2 pIy)=Px)pOIx) j=1,2:=1,2 p(y,) 要计算出p(xIy,)必须先算出py,),所以,计算互信息时一般 选用第二个等式进行计算,可得 20
20 3.1.2 信道参数 解:(1)信源 1 2 ( ) 0.6 0.4 X x x p x = 事件 1 x 含有的自信息为 1 2 2 I x p x ( ) log ( ) log 0.6 0.737bit = − = − 事件 2 x 含有的自信息为 2 2 2 I x p x ( ) log ( ) log 0.4 1.32bit = − = − (2)根据题意是计算 ( ; ) i j I x y i=1,2;j=1,2 1 1 5 ( | ) 6 p y x = 2 1 1 ( | ) 6 p y x = 1 2 3 ( | ) 4 p y x = 2 2 1 ( | ) 4 p y x = ( | ) ( | ) ( ; ) log log ( ) ( ) i j j i i j i j p x y p y x I x y p x p y = = i=1,2;j=1,2 ( ) ( ) ( | ) j i j i X p y p x p y x = ( ) ( | ) ( | ) ( ) i j i i j j p x p y x p x y p y = j=1,2 i=1,2;j=1,2 ( | ) i j p x y ( )j 要计算出 必须先算出 p y ,所以,计算互信息时一般 选用第二个等式进行计算,可得