
8,表示: 在X作用点沿X方向由 于X处的单位载荷引起 的位移。可用莫尔积分表示为: EI 对本例用莫尔积分法,或图乘法可求出 Pa (3l-a) 3EI △1P 6E1 由正则方程解出:X,= Pa (31-a) 273
11 11 表示: 在X1作用点沿X1方向由 于X1处的单位载荷引起 可用莫尔积分表示为: = l x EI M x M x d ( ) ( ) 1 1 1 1 的位移。 对本例 , 3 3 11 EI l = (3 ) 6 2 1 l a EI Pa P = − − (3 ) 2 3 2 1 l a l Pa X = − 用莫尔积分法,或图乘法可求出 由正则方程解出:
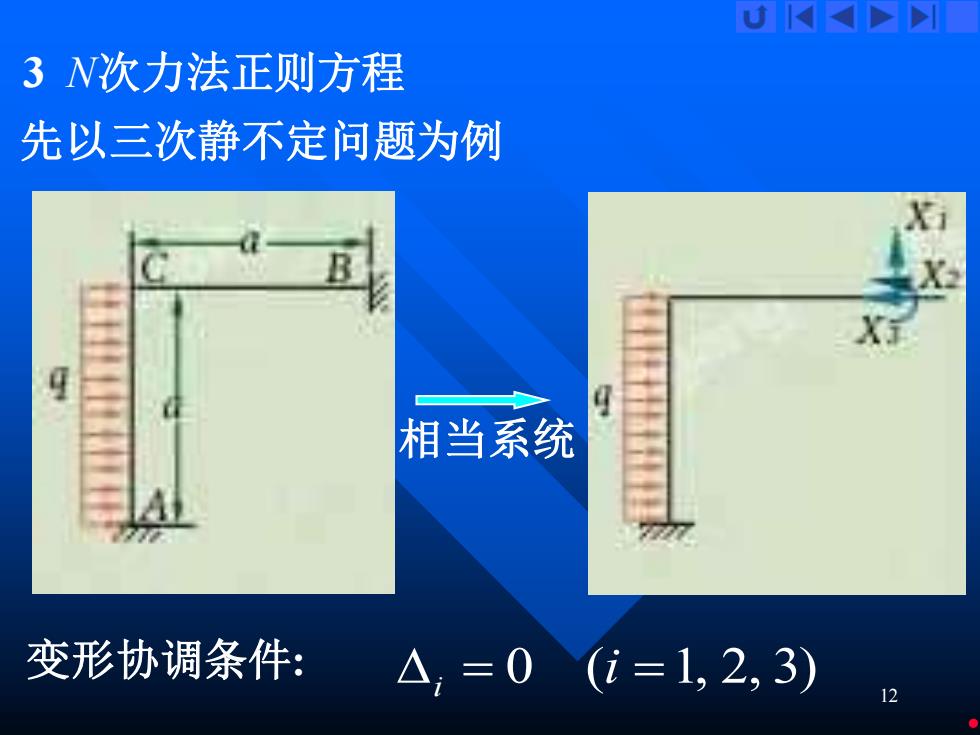
3N次力法正则方程 先以三次静不定问题为例 X行 相当系统 变形协调条件: △,=0(i=1,2,3)
12 3 N次力法正则方程 先以三次静不定问题为例 相当系统 = 0 (i =1, 2, 3) 变形协调条件 i :

变形协调条件: △,=0 (i=1,2,3) △1=δ,X1+812X2+613X3+△1P=0 △2=O21X1+822X2+d23X3+△2p=0 △3=61X1+82X2+O3X;+△3P=0 同理,对W次静不定问题,有 8,X1+δ2X2++6nXm+△ip=0 δ2X1+d22X2+…+⊙2nXm+△2p=0 δnX1+δn2X2+…+8nmXm+△P=0
13 = 0 (i =1, 2, 3) i 变形协调条件: 1 = 1 1X1 + 1 2X2 + 1 3X3 + 1P = 0 2 = 2 1X1 + 2 2X2 + 2 3X3 + 2P = 0 3 = 3 1X1 + 3 2X2 + 3 3X3 + 3P = 0 同理,对 N次静不定问题,有 Δ 0 1 1X1 + 1 2X2 ++ 1n Xn + 1P = Δ 0 2 1X1 + 2 2X2 ++ 2n Xn + 2P = Δ 0 n1 X1 + n2 X2 ++ n nXn + n P =

U K 同理,对N次静不定问题,有 δX,+612X2++δnXn+4p=0 d2X1+δ22X2+…+δ2nXn+42r=0 δniX1+δn2X2++Omn Xn+4n=0 其中的常数项△p表示: 在X作用点沿X方向由于外载荷而引起的位移。 可用莫尔积分表示为: △P dx EI
14 + + + + = + + + + = + + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 n n n n n n P n n P n n P X X X Δ X X X Δ X X X Δ 同理,对 N次静不定问题,有 其中的常数项 △iP 表示: 在Xi作用点沿Xi方向由于外载荷而引起的位移。 = l i i P x EI M x M x d ( ) ( ) 可用莫尔积分表示为:

其中的常数项△p表示: 在X作用点沿X方向由于外载荷而引起的位移。 可用莫尔积分表示为:4。=了(/回 BI 其中的系数8表示: 在X作用点沿X方向由于X处的单位载荷引起的 位移。 8可用莫尔积分表示为:⊙,= M)Mdx EI 根据位移互等定理,有: 15
15 其中的常数项 △iP 表示: 在Xi作用点沿Xi方向由于外载荷而引起的位移。 = l i i x EI M x M x d ( ) ( ) 可用莫尔积分表示为 P : 其中的系数 ij 表示: 在Xi作用点沿Xi方向由于Xj处的单位载荷引起的 位移。 根据位移互等定理,有: ij = ji ij可用莫尔积分表示为: = l i j i j x EI M x M x d ( ) ( )