
U K 3静定基和相当系统 静定基(基本静定系 静不定系统在解除某些约束后得到的静定系统 静定基不唯一。 相当系统 在静定基上作用外载荷和被解除约束的约束反 力的系统。 与静不定系统静力等效
6 3 静定基和相当系统 静定基(基本静定系) 静不定系统在解除某些约束后得到的静定系统. 静定基不唯一。 相当系统 在静定基上作用外载荷和被解除约束的约束反 力的系统。 ⎯⎯ 与静不定系统静力等效
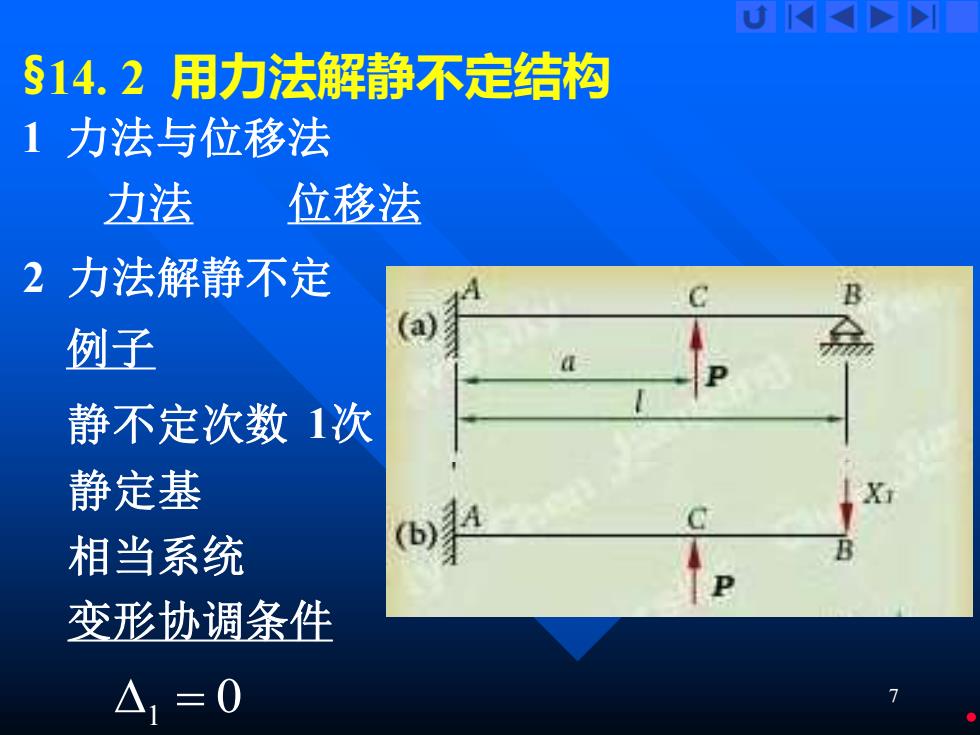
U K> §14.2用力法解静不定结构 1力法与位移法 力法 位移法 2力法解静不定 B 例子 静不定次数1次 静定基 相当系统 变形协调条件 △1=0
7 §14. 2 用力法解静不定结构 1 力法与位移法 力法 位移法 2 力法解静不定 例子 静不定次数 1次 静定基 相当系统 变形协调条件 1 = 0

U K 位移的表示 才 △1=△1P+△1x △1x的表示 X 在B点沿X的方 R 向加单位力 > δ1 对线弹性结构,有:△x=X⊙ 代入变形协调条件,得到: AP+X1·⊙1=0→δX1+△P=0
8 位移的表示 1 = 1P 1X1 + △1X1的表示 在B点沿X1的方 向加单位力 11 1 1 1 1 1 = X 对线弹性结构,有 X : 代入变形协调条件,得到: 1P 1 11 + X = 0 11X1 + 1P = 0

U K 代入变形协调条件,得到: △P+X,δ,=0→81,X1+△P=0 这就是求解一次静不定问题的力法正则方程。 其中每一项的物理意义是位移。 △1P表示: 才 在X作用点沿X方向 由于外载荷作用而引起的位移。 注意:外载荷中不包括X。 可用莫尔积分表示为AMd El
9 代入变形协调条件,得到: 1P + X1 11 = 0 这就是求解一次静不定问题的力法正则方程。 其中每一项的物理意义是位移。 11X1 + 1P = 0 △1P 表示: = l P x EI M x M x d ( ) ( ) 1 1 注意:外载荷中不包括 X1。 在X1作用点沿 X1方向 由于外载荷作用而引起的位移。 可用莫尔积分表示为:

U K δ1,X,+△1P=0 △P表示: 才P (c) 在X作用点沿X方向 由于外载荷作用而引起的位移。 注意:外载荷中不包括X。 可用览尔积分表示为:△= M()M()dx EI 8,表示: 在X作用点沿X方向由 (e) 于X处的单位载荷引起 的位移。 10
10 11X1 + 1P = 0 △1P 表示: 在 X1作用点沿 X1方向 由于外载荷作用而引起的位移。 11 表示: 在X1作用点沿X1方向由 于X1处的单位载荷引起 的位移。 = l P x EI M x M x d ( ) ( ) 1 可用莫尔积分表示为 1 : 注意:外载荷中不包括 X1