
第3卷第4期 智能系统学报 Vol 3 Ng 4 2008年8月 CAA I Transactions on Intelligent Systems Aug 2008 基于LLE的多姿态人耳识别 谢朝霞,穆志纯',谢建军2 (1.北京科技大学信息工程学院,北京100083:2河南科技大学机电工程学院,河南洛阳471003) 摘要:多姿态人耳识别是人耳识别技术面临的一个难题,目前这方面的研究并不多见.通过分析国内外2D人耳 识别方法在解决姿态问题时存在的不足,引入流形学习算法,提出一种基于局部线性嵌入的多姿态人耳识别方法 实验结果表明,这种方法在人耳姿态变化时能够取得非常理想的识别率,提高了人耳识别的鲁棒性,增强了人耳识 别技术的实用性 关键词:多姿态人耳识别;流形学习;局部线性嵌入,姿态变化 中图分类号:TP181:IP391文献标识码:A文章编号:1673-4785(2008)04032107 Multipose ear recogn ition ba sed on locally lnear em bedding XIE Zhao-xia,MU Zhi-chun',XIE Jian-jun (1.School of Infomation Engineering,University of Science and Technology Beijing,Beijing 100083,China;2 School ofMechatronics Engineering.Henan University of Science and Technolgy,Luoyang 471003,China) Abstract:Multipose ear recognition is a challenging problem in ear recognition technolgy,and it has not received sufficient attention In this paper,on the basis of the manifold leaming algorithm,we propose a multi-pose ear rec- ogniton method based on LLE(locally linear embedding )that overcomes the disadvantages of 2D ear recognition methods in dealing with pose variations Expermental results show that thismethod can obtain a satisfactorily high recognition rate,mproving the robustness of ear recognition,and enhancing the practicability of ear recognition techno logy Keywords:multi-pose ear recognition;manifold leaming LLE;pose variation 如何快速、准确地鉴定个人身份,保护信息安全脸多模态融合识别,丰富了生物特征识别技术 是当今网络信息时代所面临的关键社会问题.由于 目前的人耳识别技术一定程度上对光照、姿态 人体身体特征具有不可复制的特点,人们便把目光 等环境条件做了特定的限制,在实际中难以被广泛 转向了生物特征识别技术,希望能够应用此技术加 应用.而且现在的研究多为前视人耳图像,但是在实 强现行系统的安全性 际应用中,由于人耳与摄像机之间的角度会经常发 人耳作为一种新的生物特征,具有其独有的自 生变化,获取正面人耳图像存在一定难度.此外,当 身特点:丰富和稳定的结构特征,这些特征在人 人耳姿态发生变化时,人耳形状会产生不同程度的 生的相当长一段时间内都保持不变,人耳特征不受 形变,现有的2D人耳图像识别技术存在其局限性 表情变化的影响;而且人耳的特定生理位置使其紧 因此,为了提高人耳识别的鲁棒性,满足实际应用的 靠的背景可以预测.鉴于人耳独特的生理结构和生 需要,必须放松对姿态条件的限制,研究多姿态人耳 理位置,人耳识别技术不仅可以单独应用于一些个 识别技术势在必行 体识别场合,而且还可以和其他生物特征识别技术 1人耳识别研究现状 互为补充,构成多模态生物特征识别技术,如人耳人 近年来,国内外基于2D图像的人耳识别方法 收稿日期:200803-19 可大体分为2类:基于几何特征的人耳识别方法和 基金项目:国家自然科学基金资助项目(60375002,60573058):北京 市教委重点学科共建项目(XK100080537). 基于代数特征的人耳识别方法,如表1所示. 通信作者:谢朝霞.Email xiezhaox@163.com 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 3卷第 4期 智 能 系 统 学 报 Vol. 3 №. 4 2008年 8月 CAA I Transactions on Intelligent System s Aug. 2008 基于 LLE的多姿态人耳识别 谢朝霞 1 ,穆志纯 1 ,谢建军 2 (1. 北京科技大学 信息工程学院 ,北京 100083; 2. 河南科技大学 机电工程学院 ,河南 洛阳 471003) 摘 要 :多姿态人耳识别是人耳识别技术面临的一个难题 ,目前这方面的研究并不多见. 通过分析国内外 22D人耳 识别方法在解决姿态问题时存在的不足 ,引入流形学习算法 ,提出一种基于局部线性嵌入的多姿态人耳识别方法. 实验结果表明 ,这种方法在人耳姿态变化时能够取得非常理想的识别率 ,提高了人耳识别的鲁棒性 ,增强了人耳识 别技术的实用性. 关键词 :多姿态人耳识别 ;流形学习 ;局部线性嵌入 ;姿态变化 中图分类号 : TP181; TP391 文献标识码 : A 文章编号 : 167324785 (2008) 0420321207 M ulti2pose ear recogn ition based on locally linear embedding X IE Zhao2xia 1 , MU Zhi2chun 1 , X IE Jian2jun 2 (1. School of Information Engineering, University of Science and TechnologyBeijing, Beijing 100083, China; 2. School ofMechatronics Engineering, Henan University of Science and Technology, Luoyang 471003, China) Abstract:Multi2pose ear recognition is a challenging p roblem in ear recognition technology, and it has not received sufficient attention. In this paper, on the basis of the manifold learning algorithm, we p ropose a multi2pose ear rec2 ognition method based on LLE ( locally linear embedding ) that overcomes the disadvantages of 22D ear recognition methods in dealing with pose variations. Experimental results show that thismethod can obtain a satisfactorily high recognition rate, imp roving the robustness of ear recognition, and enhancing the p racticability of ear recognition technology. Keywords:multi2pose ear recognition; manifold learning; LLE; pose variation 收稿日期 : 2008203219. 基金项目 :国家自然科学基金资助项目 ( 60375002, 60573058) ;北京 市教委重点学科共建项目 (XK100080537). 通信作者 :谢朝霞. E2mail: xiezhaox@163. com. 如何快速、准确地鉴定个人身份 ,保护信息安全 是当今网络信息时代所面临的关键社会问题. 由于 人体身体特征具有不可复制的特点 ,人们便把目光 转向了生物特征识别技术 ,希望能够应用此技术加 强现行系统的安全性. 人耳作为一种新的生物特征 ,具有其独有的自 身特点 [ 1 ] :丰富和稳定的结构特征 ,这些特征在人 生的相当长一段时间内都保持不变 ;人耳特征不受 表情变化的影响 ;而且人耳的特定生理位置使其紧 靠的背景可以预测. 鉴于人耳独特的生理结构和生 理位置 ,人耳识别技术不仅可以单独应用于一些个 体识别场合 ,而且还可以和其他生物特征识别技术 互为补充 ,构成多模态生物特征识别技术 ,如人耳人 脸多模态融合识别 ,丰富了生物特征识别技术. 目前的人耳识别技术一定程度上对光照、姿态 等环境条件做了特定的限制 ,在实际中难以被广泛 应用. 而且现在的研究多为前视人耳图像 ,但是在实 际应用中 ,由于人耳与摄像机之间的角度会经常发 生变化 ,获取正面人耳图像存在一定难度. 此外 ,当 人耳姿态发生变化时 ,人耳形状会产生不同程度的 形变 ,现有的 2D人耳图像识别技术存在其局限性. 因此 ,为了提高人耳识别的鲁棒性 ,满足实际应用的 需要 ,必须放松对姿态条件的限制 ,研究多姿态人耳 识别技术势在必行. 1 人耳识别研究现状 近年来 ,国内外基于 22D图像的人耳识别方法 可大体分为 2类 :基于几何特征的人耳识别方法和 基于代数特征的人耳识别方法 ,如表 1所示. © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

·322· 智能系统学报 第3卷 表12D人耳识别方法 姿态变化较大时,识别率将急剧下降 Table 1 2D ear recogn ition methods 基于代数特征的人耳识别方法,从人耳图像的 特征分类 识别方法 代表研究 整体出发,提取反映人耳的特征.PCA1被认为是最 lannarelli人耳识别 12段测量法 成功的线性鉴别分析方法之一,本质上PCA方法的 N-graph曲线邻接关系 Voronoi相邻图 目的是在最小均方意义下寻找最能代表原始数据的 神经网络法 外耳轮廓点和耳形特征 投影.独立分量分析是基于高阶统计特性的分析方 几何特征 力场转换法 势能井和势能通道 法,C4的目标就是利用一种线性变换,分离出独 LABSSFEM 外耳形状和内耳结构 立主元,使得图像中的统计依赖性消失或减到最小 傅立叶方法 入耳轮廓特征 程度.但是当样本点具有非线性性质时,采用线性方 PCA 人耳识别与人脸识别的比较 法无法反映出样本点之间所隐藏的非线性性质.文 不变矩法 高阶不变矩提取特征 献【12表明,当光照、姿态变化时,人脸图像在高维 代数特征 CA 高阶统计特征 观测空间呈现出高度的非线性流形结构.同样,当光 核Fisher 核Fisher KPCA KPCA 照、姿态变化时,人耳图像也具有这种非线性性质 因此,PCA、CA等线性方法存在一定的局限性 1.1基于几何特征的人耳识别 基于核技巧的人耳识别方法的基本思想四是 最具有代表性的早期研究是A.lannarelli提出 通过一个非线性变换把输入数据映射到一个高维特 的基于I2个测量段为特征的lannarelli系统2).这 征空间,使得原本在输入空间无法线性分类的数据 种方法以人耳解剖学点作为测量系统的基础,所有 变换到特征空间来实现线性分类.这种方法虽然可 的测量都取决于原点的精确定位,因此不适用于计 以对非线性数据进行分类识别,但是需要在图像预 算机视觉;Moreno!1等分别提出了基于外耳特征点、 处理阶段对人耳图像进行角度、光照归一化,以消除 基于外耳形态学分析和基于宏观特征的压缩网络的 由于姿态、光照所带来的影响,因而在一定程度上也 识别方法,同时又通过复合分类技术将上述3种方 易受姿态、光照的影响.文献【11的实验结果表明, 法组合进行人耳识别;Burge和Burge首先构造人 当发生角度和光照变化时,在USB图像库2(带角 耳边缘曲线的Voronoil图,然后提取相邻曲线的关 度和光照变化的图像库)上的识别率急剧下降,特 系来构造特征向量进行识别,Hurley,N ixon和Carter 征空间取70维,识别率取得最大值为54% 等56)使用力场转换方法提取人耳图像的势能通道 经过上述分析可以看出,目前人耳识别所采用 和势能井,并将它们的位置作为人耳描述特征进行 的各种方法,在解决人耳姿态问题时都存在其局限 识别:刘炜杰等使用基于傅里叶系数的方法对人 性.流形学习作为一种新的基于拓扑学的非线性方 耳轮廓进行识别;M心等提出了基于外耳轮廓形状 法,从人类认知角度出发1,通过研究高维数据集 特征和内耳结构特征(long axis based shape and 的内在几何结构,发现其内在几何规律,能够更好地 structural feature extraction method,LAB SSFEM) 解决数据的非线性问题,.比起前面的各种方法, 耳识别方法,但是这种方法仅适用于正面人耳图像. 流形学习在解决姿态问题上具有明显的优势,它能 通过以上论述,可以看出,基于几何特征的人耳 够很好地发现高维数据集的结构,提供更好的数据 识别方法首先需要提取外耳边缘和内耳轮廓,这就 理解.作为流形学习谱方法中的一种,近年来提出一 决定了这些方法必定易受光照、姿态等因素的影响, 种称之为局部线性嵌入1的流形学习算法,它通过 特征提取不稳定」 非线性维数约简方式,获得高维数据的有代表性的 12基于代数特征的人耳识别 最佳低维投影 Vico等应用标准主元分析法(PCA)对人耳 2局部线性嵌入 进行识别,并与人脸识别进行比较,实验结果均为人 脸识别结果优于人耳识别:王忠礼9等采用高阶不变 21算法简介 矩方法提取人耳图像特征,并提出基于不变矩的改进 局部线性嵌入(locally linear embedding, 算法,可一定程度上克服人耳图像因为平移、缩放等 LE)167是一种非线性降维算法,其基本思想是保 因素造成的图像失真对识别结果的影响;张海军1、 持原流形中局部邻域间相互关系,将高维数据映射 袁立II等分别采用CA核Fisher与核PCA方法,在 到低维全局坐标系中,即把N个样本的数据集 USB自建人耳库上进行识别,实验结果表明当人耳 X,∈R映射到低维向量Y,1∈R.LE的 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
表 1 2D人耳识别方法 Table 1 2D ear recogn ition m ethods 特征分类 识别方法 代表研究 几何特征 Iannarelli人耳识别 N2graph曲线邻接关系 神经网络法 力场转换法 LABSSFEM 傅立叶方法 12段测量法 Voronoi相邻图 外耳轮廓点和耳形特征 势能井和势能通道 外耳形状和内耳结构 入耳轮廓特征 代数特征 PCA 不变矩法 ICA 核 Fisher KPCA 人耳识别与人脸识别的比较 高阶不变矩提取特征 高阶统计特征 核 Fisher KPCA 1. 1 基于几何特征的人耳识别 最具有代表性的早期研究是 A. Iannarelli提出 的基于 12个测量段为特征的 Iannarelli系统 [ 2 ] . 这 种方法以人耳解剖学点作为测量系统的基础 ,所有 的测量都取决于原点的精确定位 ,因此不适用于计 算机视觉 ;Moreno [ 3 ]等分别提出了基于外耳特征点、 基于外耳形态学分析和基于宏观特征的压缩网络的 识别方法 ,同时又通过复合分类技术将上述 3种方 法组合进行人耳识别 ; Burge和 Burger [ 4 ]首先构造人 耳边缘曲线的 Voronoi图 ,然后提取相邻曲线的关 系来构造特征向量进行识别 ; Hurley、N ixon和 Carter 等 [ 526 ]使用力场转换方法提取人耳图像的势能通道 和势能井 ,并将它们的位置作为人耳描述特征进行 识别 ;刘炜杰等 [ 7 ]使用基于傅里叶系数的方法对人 耳轮廓进行识别 ;Mu [ 1 ]等提出了基于外耳轮廓形状 特征和内耳结构特征 ( long axis based shape and structural feature extraction method, LABSSFEM )的人 耳识别方法 ,但是这种方法仅适用于正面人耳图像. 通过以上论述 ,可以看出 ,基于几何特征的人耳 识别方法首先需要提取外耳边缘和内耳轮廓 ,这就 决定了这些方法必定易受光照、姿态等因素的影响 , 特征提取不稳定. 1. 2 基于代数特征的人耳识别 V ictor等 [ 8 ]应用标准主元分析法 (PCA )对人耳 进行识别 ,并与人脸识别进行比较 ,实验结果均为人 脸识别结果优于人耳识别;王忠礼 [ 9 ]等采用高阶不变 矩方法提取人耳图像特征 ,并提出基于不变矩的改进 算法 ,可一定程度上克服人耳图像因为平移、缩放等 因素造成的图像失真对识别结果的影响;张海军 [ 10 ]、 袁立 [ 11 ]等分别采用 ICA、核 Fisher与核 PCA方法 ,在 USTB自建人耳库上进行识别 ,实验结果表明当人耳 姿态变化较大时 ,识别率将急剧下降. 基于代数特征的人耳识别方法 ,从人耳图像的 整体出发 ,提取反映人耳的特征. PCA [ 8 ]被认为是最 成功的线性鉴别分析方法之一 ,本质上 PCA方法的 目的是在最小均方意义下寻找最能代表原始数据的 投影. 独立分量分析是基于高阶统计特性的分析方 法 , ICA [ 10 ]的目标就是利用一种线性变换 ,分离出独 立主元 ,使得图像中的统计依赖性消失或减到最小 程度. 但是当样本点具有非线性性质时 ,采用线性方 法无法反映出样本点之间所隐藏的非线性性质. 文 献 [ 12 ]表明 ,当光照、姿态变化时 ,人脸图像在高维 观测空间呈现出高度的非线性流形结构. 同样 ,当光 照、姿态变化时 ,人耳图像也具有这种非线性性质. 因此 , PCA、ICA等线性方法存在一定的局限性. 基于核技巧的人耳识别方法的基本思想 [ 11 ]是 通过一个非线性变换把输入数据映射到一个高维特 征空间 ,使得原本在输入空间无法线性分类的数据 变换到特征空间来实现线性分类. 这种方法虽然可 以对非线性数据进行分类识别 ,但是需要在图像预 处理阶段对人耳图像进行角度、光照归一化 ,以消除 由于姿态、光照所带来的影响 ,因而在一定程度上也 易受姿态、光照的影响. 文献 [ 11 ]的实验结果表明 , 当发生角度和光照变化时 ,在 USTB图像库 2 (带角 度和光照变化的图像库 )上的识别率急剧下降 ,特 征空间取 70维 ,识别率取得最大值为 54%. 经过上述分析可以看出 ,目前人耳识别所采用 的各种方法 ,在解决人耳姿态问题时都存在其局限 性. 流形学习作为一种新的基于拓扑学的非线性方 法 ,从人类认知角度出发 [ 13 ] ,通过研究高维数据集 的内在几何结构 ,发现其内在几何规律 ,能够更好地 解决数据的非线性问题 [ 14 ] . 比起前面的各种方法 , 流形学习在解决姿态问题上具有明显的优势 ,它能 够很好地发现高维数据集的结构 ,提供更好的数据 理解. 作为流形学习谱方法中的一种 ,近年来提出一 种称之为局部线性嵌入 [ 15 ]的流形学习算法 ,它通过 非线性维数约简方式 ,获得高维数据的有代表性的 最佳低维投影. 2 局部线性嵌入 2. 1 算法简介 局 部 线 性 嵌 入 ( locally linear embedding, LLE) [ 16217 ]是一种非线性降维算法 ,其基本思想是保 持原流形中局部邻域间相互关系 ,将高维数据映射 到低维全局坐标系中 , 即把 N 个样本的数据集 { Xi } N i = 1 ∈R D 映射到低维向量 { Yi } N i = 1 ∈R d . LLE的 · 223 · 智 能 系 统 学 报 第 3卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net

第4期 谢朝霞,等:基于LE的多姿态人耳识别 ·323 具体算法分3步: 1)邻域选择:计算每个样本点X,的邻域点陬 距离最近的K个邻域点或固定半径ε的球状邻 域: 2计算重构权值矩阵W,:在X,的邻域中,计算 能最好地重构每个X,的权值矩阵W使重构误差 Ew)=∑x·∑,wgx最小其中,权值矩 阵W要满足2个约束条件:1)每一个数据点X,都 只能由它的邻近点来表示,若X,不是近邻点,则W, 为零矩阵;2)权值矩阵W的每一行的和为1这样, 求解最优权值就转化为重构误差EW)在约束条件 09 下的最小二乘问题: 0.5 3计算d维嵌入值Y,:根据权值矩阵W,重构 0 每个数据点的低维嵌入向量Y,使得重构误差 中(Y)最小: (a)S-Curve曲线 Φy=¥-∑w,Y (1) 1.5 为了保证式(1)能得到惟一解,低维嵌入Y,需 满足2个约束条件:1) ∑Y,为零矩阵: 0.5 2¥¥=1 LLE的优点在于:1)待定参数少,只有K和d -0. 2)具有整体最优解,不需要迭代,避免了局部极值 问题:3)嵌入向量的求解归结为求解稀疏矩阵的特 征向量,计算复杂度较低,容易执行」 图1给出了LE在人工合成数据上的低维嵌 20 入实例.在R空间中的S-Curve曲面上,随机选取 2000个数据点,邻域大小K=37,低维嵌入维数d= 2,采用LLE获取该数据集的最佳2维嵌入,结果如 2s-40-030010152025 图1(b)所示 2.2参数的选择 (b)二维嵌入结果 LLE算法中待定参数只有K和d然而这2个 图1LLE低维嵌入 Fig 1 Low dmensional embedding using LLE 参数的选择却对后续操作有着至关重要的影响。 221K的选择 直接影响低维嵌入映射的好坏 选择合理的K值,是LLE算法的关键问题之 222d的选择 一,K值过大1,可能会导致不能正确表示其局部 和K一样,d的选择是LE算法的另一个关键 几何关系;相反,K值过小,将会导致将连续流形分 问题.从直观角度考虑,K取值越大,说明对每个数 割为不相交的子流形 据点的描述信息越丰富,所需的自由变量的数目也 图2分别给出图1(a)中S-Cuve曲面在低维嵌 越多,参数d的取值也应增大.但是对于有限样本容 入维数相同时,即d=2,不同K值得到的低维嵌入 量,数据点在高维空间通常呈现出高度稀疏性,d取 映射 值过大显然不合理.因此,合理选择d值,是一个值 对比图1、图2可以看出,选取K=37图1)所 得考虑的问题 得到的2维嵌入结果显然要优于K取值分别为5、 图3分别给出图1(a)中S-Cuve曲面在邻域大 15、25和40时图2)的嵌入结果.这表明K取值不 小相同时,即K=37,不同d得到的低维嵌入结果 同,得到的低维嵌入结果也不同.K取值的合理与否 由于当d>3时,低维嵌入映射呈现在维数大于 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.htp://www.cnki.net
具体算法分 3步 : 1)邻域选择 :计算每个样本点 Xi 的邻域点 (取 距离最近的 K个邻域点或固定半径 ε的球状邻 域 ) ; 2)计算重构权值矩阵 W ij:在 Xi 的邻域中 ,计算 能最好地重构每个 Xi 的权值矩阵 W ij ,使重构误差 E (W ) = ∑i Xi - ∑j W ijXj 2 最小. 其中 ,权值矩 阵 W ij要满足 2个约束条件 : 1)每一个数据点 Xi 都 只能由它的邻近点来表示 ,若 Xj不是近邻点 ,则 W ij 为零矩阵; 2)权值矩阵 W ij的每一行的和为 1. 这样 , 求解最优权值就转化为重构误差 E (W )在约束条件 下的最小二乘问题; 3)计算 d维嵌入值 Yi:根据权值矩阵 W ij ,重构 每个数据点的低维嵌入向量 Yi , 使得重构误差 Φ ( Y)最小 : Φ ( Y) = ∑i Yi - ∑j W ij Yj 2 . (1) 为了保证式 (1)能得到惟一解 ,低维嵌入 Yi 需 满 足 2 个 约 束 条 件 : 1 ) ∑i Yi 为 零 矩 阵; 2) 1 N ∑ i Yi Y T i = I. LLE的优点在于 : 1)待定参数少 ,只有 K和 d; 2)具有整体最优解 ,不需要迭代 ,避免了局部极值 问题; 3)嵌入向量的求解归结为求解稀疏矩阵的特 征向量 ,计算复杂度较低 ,容易执行. 图 1给出了 LLE在人工合成数据上的低维嵌 入实例. 在 R 3 空间中的 S2Curve曲面上 ,随机选取 2 000个数据点 ,邻域大小 K = 37,低维嵌入维数 d = 2,采用 LLE获取该数据集的最佳 2维嵌入 ,结果如 图 1 ( b)所示. 2. 2 参数的选择 LLE算法中待定参数只有 K和 d,然而这 2个 参数的选择却对后续操作有着至关重要的影响. 2. 2. 1 K的选择 选择合理的 K值 , 是 LLE算法的关键问题之 一. K值过大 [ 18 ] ,可能会导致不能正确表示其局部 几何关系 ;相反 , K值过小 ,将会导致将连续流形分 割为不相交的子流形. 图 2分别给出图 1 ( a)中 S2Curve曲面在低维嵌 入维数相同时 ,即 d = 2,不同 K值得到的低维嵌入 映射. 对比图 1、图 2可以看出 ,选取 K = 37 (图 1)所 得到的 2维嵌入结果显然要优于 K取值分别为 5、 15、25和 40时 (图 2)的嵌入结果. 这表明 K取值不 同 ,得到的低维嵌入结果也不同. K取值的合理与否 ( a) S2Curve曲线 ( b)二维嵌入结果 图 1 LLE低维嵌入 Fig. 1 Low dimensional embedding using LLE 直接影响低维嵌入映射的好坏. 2. 2. 2 d的选择 和 K一样 , d的选择是 LLE算法的另一个关键 问题. 从直观角度考虑 , K取值越大 ,说明对每个数 据点的描述信息越丰富 ,所需的自由变量的数目也 越多 ,参数 d的取值也应增大. 但是对于有限样本容 量 ,数据点在高维空间通常呈现出高度稀疏性 , d取 值过大显然不合理. 因此 ,合理选择 d值 ,是一个值 得考虑的问题. 图 3分别给出图 1 ( a)中 S2Curve曲面在邻域大 小相同时 ,即 K = 37,不同 d得到的低维嵌入结果. 由于当 d > 3时 ,低维嵌入映射呈现在维数大于 第 4期 谢朝霞 ,等 :基于 LLE的多姿态人耳识别 · 323 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
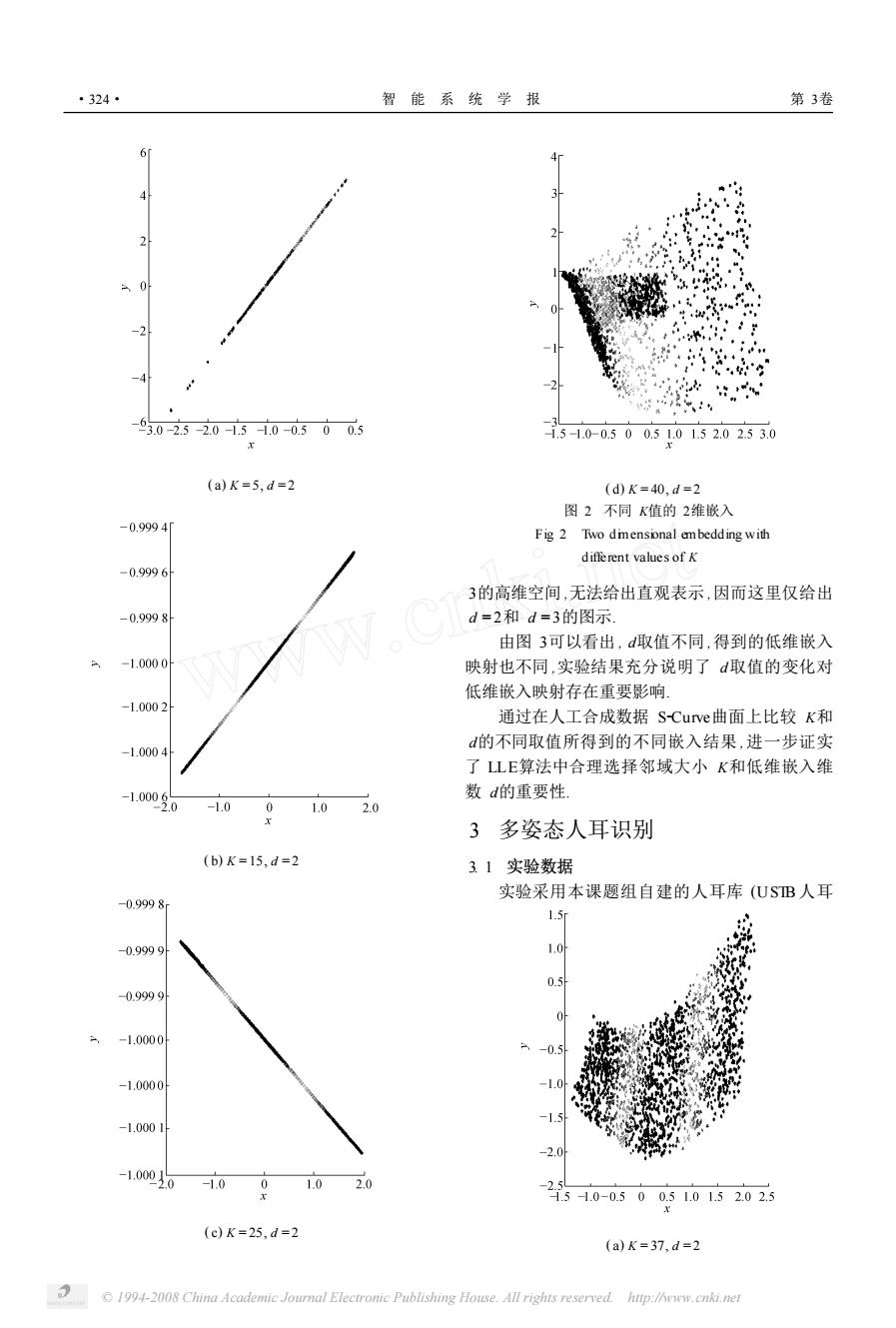
·324 智能系统学报 第3卷 6 4 2 0 -2 -4 修 -3.0=2.52.0151.0-0.500.5 1.5-1.0-0.500.51.01.52.02.53.0 文 (a)K=5,d=2 (d)K=40,d=2 图2不同K值的2维嵌入 -0.9994 Fig 2 Two dmensional embedding with different values of K -0.9996 3的高维空间,无法给出直观表示,因而这里仅给出 -0.9998 d=2和d=3的图示 由图3可以看出,d取值不同,得到的低维嵌入 -1.0000 映射也不同,实验结果充分说明了d取值的变化对 低维嵌入映射存在重要影响. -1.0002 通过在人工合成数据S-Curve曲面上比较K和 d的不同取值所得到的不同嵌入结果,进一步证实 -1.0004 了LE算法中合理选择邻域大小K和低维嵌入维 -1.0006 数d的重要性 -2.0 -1.0 01.0 2.0 3多姿态人耳识别 (b)K=15,d=2 31实验数据 实验采用本课题组自建的人耳库(USB人耳 -0.9998 1.5 0.9999 1.0 0.5 0.9999 -1.0000 -1.0000 -1.0001 -100020 -1.001.02.0 2.5 1 1.51.0-0.500.51.01.52.02.5 (c)K=25,d=2 (a)K=37,d=2 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.nei
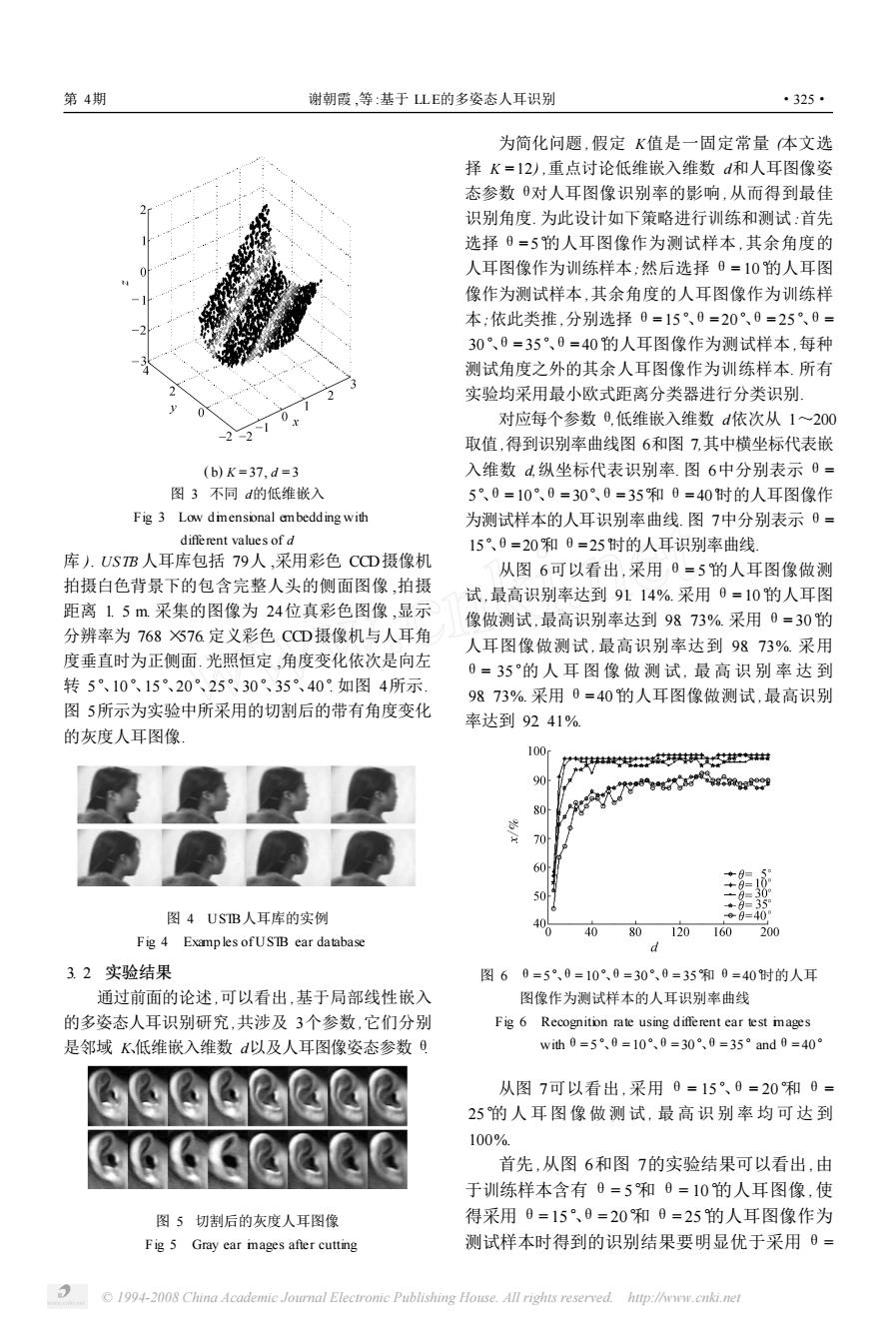
( a) K = 5, d = 2 ( b) K = 15, d = 2 ( c) K = 25, d = 2 ( d) K = 40, d = 2 图 2 不同 K值的 2维嵌入 Fig. 2 Two dimensional embedding with different values of K 3的高维空间 ,无法给出直观表示 ,因而这里仅给出 d = 2和 d = 3的图示. 由图 3可以看出 , d取值不同 ,得到的低维嵌入 映射也不同 ,实验结果充分说明了 d取值的变化对 低维嵌入映射存在重要影响. 通过在人工合成数据 S2Curve曲面上比较 K和 d的不同取值所得到的不同嵌入结果 ,进一步证实 了 LLE算法中合理选择邻域大小 K和低维嵌入维 数 d的重要性. ( a) K = 37, d = 2 3 多姿态人耳识别 3. 1 实验数据 实验采用本课题组自建的人耳库 (USTB 人耳 · 423 · 智 能 系 统 学 报 第 3卷 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net
第4期 谢朝霞,等:基于LE的多姿态人耳识别 ·325· 为简化问题,假定K值是一固定常量(本文选 择K=12),重点讨论低维嵌入维数d和人耳图像姿 态参数对人耳图像识别率的影响,从而得到最佳 识别角度.为此设计如下策略进行训练和测试:首先 选择0=5的人耳图像作为测试样本,其余角度的 人耳图像作为训练样本:然后选择0=10的人耳图 像作为测试样本,其余角度的人耳图像作为训练样 本:依此类推,分别选择0=15°、0=20°、0=25°、0= 30°、0=35°、0=40的人耳图像作为测试样本,每种 测试角度之外的其余人耳图像作为训练样本.所有 实验均采用最小欧式距离分类器进行分类识别. 0 对应每个参数0,低维嵌入维数d依次从1~200 2 取值,得到识别率曲线图6和图7,其中横坐标代表嵌 (b)K=37,d=3 入维数d纵坐标代表识别率.图6中分别表示0= 图3不同d的低维嵌入 5°、0=10°、0=30°、0=35和0=40时的人耳图像作 Fig 3 Low dmensional embedding with 为测试样本的人耳识别率曲线.图7中分别表示= different values of d 15°0=20和0-25时的人耳识别率曲线. 库人.USB人耳库包括79人,采用彩色CCD摄像机 从图6可以看出,采用0=5的人耳图像做测 拍摄白色背景下的包含完整人头的侧面图像,拍摄 试,最高识别率达到9114%.采用0=10的人耳图 距离15m采集的图像为24位真彩色图像,显示 像做测试,最高识别率达到9873%.采用日=30的 分辨率为768576定义彩色CCD摄像机与人耳角 人耳图像做测试,最高识别率达到9873%.采用 度垂直时为正侧面.光照恒定,角度变化依次是向左 0=35°的人耳图像做测试,最高识别率达到 转5°、10°、15°、20°25°、30°、35°、40°如图4所示. 9873%.采用0=40的人耳图像做测试,最高识别 图5所示为实验中所采用的切割后的带有角度变化 率达到9241% 的灰度人耳图像 100 线特转纯共代实进# 90 的pgpoo 70 60 50 08=35 图4USB人耳库的实例 60=40 Fig 4 Examples ofUSTB ear database 40640 80120160200 3.2实验结果 图60=5°、0=10°、0=30°、0=35和0=40时的人耳 通过前面的论述,可以看出,基于局部线性嵌入 图像作为测试样本的人耳识别率曲线 的多姿态人耳识别研究,共涉及3个参数,它们分别 Fig 6 Recognition rate using different ear test mages 是邻域K低维嵌入维数d以及人耳图像姿态参数日 with0=5°、0=10°、0=30°、0=35°and0=40 从图7可以看出,采用0=15°、0=20和0= 25的人耳图像做测试,最高识别率均可达到 100%. 首先,从图6和图7的实验结果可以看出,由 于训练样本含有日=5和日=10的人耳图像,使 图5切割后的灰度人耳图像 得采用0=15°、0=20和0=25的人耳图像作为 Fig 5 Gray ear mages after cutting 测试样本时得到的识别结果要明显优于采用日= 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
( b) K = 37, d = 3 图 3 不同 d的低维嵌入 Fig. 3 Low dimensional embedding with different values of d 库 ). USTB 人耳库包括 79人 ,采用彩色 CCD摄像机 拍摄白色背景下的包含完整人头的侧面图像 ,拍摄 距离 1. 5 m. 采集的图像为 24位真彩色图像 ,显示 分辨率为 768 ×576. 定义彩色 CCD摄像机与人耳角 度垂直时为正侧面. 光照恒定 ,角度变化依次是向左 转 5°、10°、15°、20°、25°、30°、35°、40°. 如图 4所示. 图 5所示为实验中所采用的切割后的带有角度变化 的灰度人耳图像. 图 4 USTB人耳库的实例 Fig. 4 Examp les of USTB ear database 图 5 切割后的灰度人耳图像 Fig. 5 Gray ear images after cutting 3. 2 实验结果 通过前面的论述,可以看出 ,基于局部线性嵌入 的多姿态人耳识别研究,共涉及 3个参数 ,它们分别 是邻域 K、低维嵌入维数 d以及人耳图像姿态参数θ. 为简化问题 ,假定 K值是一固定常量 (本文选 择 K = 12) ,重点讨论低维嵌入维数 d和人耳图像姿 态参数 θ对人耳图像识别率的影响 ,从而得到最佳 识别角度. 为此设计如下策略进行训练和测试 :首先 选择 θ= 5°的人耳图像作为测试样本 ,其余角度的 人耳图像作为训练样本;然后选择 θ= 10°的人耳图 像作为测试样本 ,其余角度的人耳图像作为训练样 本;依此类推 ,分别选择 θ= 15°、θ= 20°、θ= 25°、θ= 30°、θ= 35°、θ= 40°的人耳图像作为测试样本 ,每种 测试角度之外的其余人耳图像作为训练样本. 所有 实验均采用最小欧式距离分类器进行分类识别. 对应每个参数θ,低维嵌入维数 d依次从 1~200 取值,得到识别率曲线图 6和图 7,其中横坐标代表嵌 入维数 d,纵坐标代表识别率. 图 6中分别表示 θ= 5°、θ= 10°、θ= 30°、θ= 35°和 θ= 40°时的人耳图像作 为测试样本的人耳识别率曲线. 图 7中分别表示 θ= 15°、θ=20°和θ=25°时的人耳识别率曲线. 从图 6可以看出 ,采用 θ= 5°的人耳图像做测 试 ,最高识别率达到 91. 14%. 采用 θ= 10°的人耳图 像做测试 ,最高识别率达到 98. 73%. 采用 θ= 30°的 人耳图像做测试 , 最高识别率达到 98. 73%. 采用 θ= 35°的 人 耳 图 像 做 测 试 , 最 高 识 别 率 达 到 98. 73%. 采用 θ= 40°的人耳图像做测试 ,最高识别 率达到 92. 41%. 图 6 θ= 5°、θ= 10°、θ= 30°、θ= 35°和 θ= 40°时的人耳 图像作为测试样本的人耳识别率曲线 Fig. 6 Recognition rate using different ear test images withθ= 5°、θ= 10°、θ= 30°、θ= 35°andθ= 40° 从图 7可以看出 , 采用 θ= 15°、θ= 20°和 θ= 25°的 人 耳 图 像 做 测 试 , 最 高 识 别 率 均 可 达 到 100%. 首先 ,从图 6和图 7的实验结果可以看出 ,由 于训练样本含有 θ= 5°和 θ= 10°的人耳图像 ,使 得采用 θ= 15°、θ= 20°和 θ= 25°的人耳图像作为 测试样本时得到的识别结果要明显优于采用 θ= 第 4期 谢朝霞 ,等 :基于 LLE的多姿态人耳识别 · 523 · © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net