
JPKIC 结构设计原理 S 7.2.2 Size limits of eccentricity jhepniiplestncturedesgn Limit damage:Tensile reinforcement reached yield strain,the pressure has just reached the limit of concrete compressive strain and crushed. cu a” a 5≤56 When the hehmethehdedeataictioofof As large eccentric compression, Geometric Xb 当5>56时, axis__ ho 为小偏心受压破坏。 As e Es>Ey ec=0.002 Figure 7-5 eccentric compression strain distribution of the cross section
§7.2.2 Size limits of eccentricity Limit damage: Tensile reinforcement reached yield strain, the pressure has just reached the limit of concrete compressive strain and crushed. Figure 7-5 eccentric compression strain distribution of the cross section As As ’ a Geometric axis b r c d e f εcu εy εc = 0.002 εs>εy h0 xb a’’ a’ 为小偏心受压破坏。 b b 当 时, When the @ when the destruction of large eccentric compression, 为小偏心受压破坏。 b b 当 时, When the when the destruction of large eccentric compression

JPKIC 结构设计原理 The principle of structure design S7.2.3 Eccentric structure of the correlation curve 1)When the (M-N)on the curve or curve aba falls outside the occurrence of damage to the cross section. 2) e-M-1ge,bigeer,emore bieger. 3)Three feature points(a、b、c)
1) When the on the curve or curve falls outside the occurrence of damage to the cross section. (M − N) abd tg, N 2) e = M = bigger, e more bigger。 3) Three feature points(a、b、c) §7.2.3 Eccentric structure of the correlation curve

JPKIC 结构设计原理 Tfeprniipledistnctiredesign 4)M-N curves Ab segment (tensile failure above):An increase in axial pressure to increase their flexural capacity N d(Mu,Nu) 受压 坏 Cb section(compression failure section):An increase in axial pressure to reduce the bending capacity. 破 M
4) M-N curves Cb section (compression failure section): An increase in axial pressure to reduce the bending capacity. Ab segment (tensile failure above): An increase in axial pressure to increase their flexural capacity

JIPKIC 结构设计原理 The principle of structure design S7.3 Vertical Eccentric Compression Bending Reinforced concrete compression members under eccentric loads in,it will have a vertical bending,which will produce lateral deflection.Because the impact of lateral deflection,the cross section is no longer the moment suffered,and become a N(eo+u) that is, l/2 Neo M=N(e+w)=N(eo+四 eo =nNeo eo Known as the additional momene) /2 The impact of the additional bending moment for different slenderness ratio of eccentric compression, damage type is also different. N Figure 7-7 eccentric compression of the type sought
Reinforced concrete compression members under eccentric loads in, it will have a vertical bending, which will produce lateral deflection. Because the impact of lateral deflection, the cross section is no longer the moment suffered, and become a , that is,: Ne0 ( ) 0 N e +u 0 0 0 0 0 ( ) ( ) e Ne e e u M N e u N = + = + = Nu Known as the additional moment (M ) The impact of the additional bending moment for different slenderness ratio of eccentric compression, damage type is also different. N Figure 7-7 eccentric compression of the type sought y y u l/2 l/2 x N §7.3 Vertical Eccentric Compression Bending
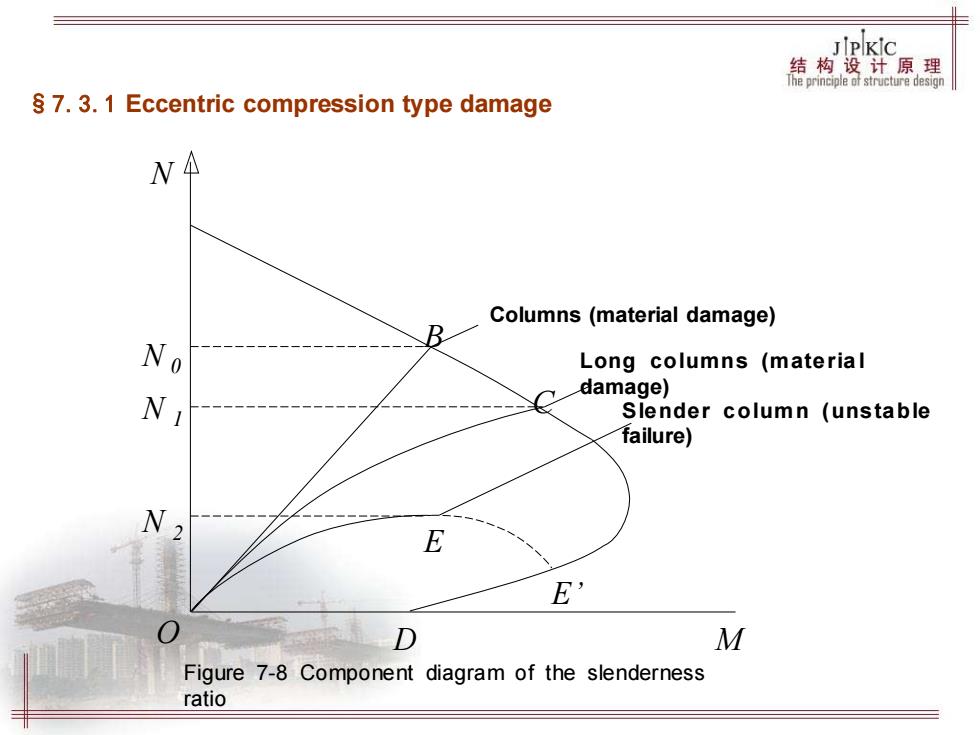
JPKIC 结构设计原理 hepniiplestncturedesgn $7.3.1 Eccentric compression type damage Columns(material damage) No Long columns (material damage) Slender column (unstable failure) E E D M Figure 7-8 Component diagram of the slenderness ratio
B C Columns (material damage) Long columns (materia l damage) Slender column (unstable failure) N 0 N 1 N 2 E O D M E’ Figure 7-8 Component diagram of the slenderness ratio N §7.3.1 Eccentric compression type damage