效绵 So far... some language {anbn|n≥0} decidable all languages regular languages context free languages RE {abcn|n≥0} We will show a natural undecidable L next
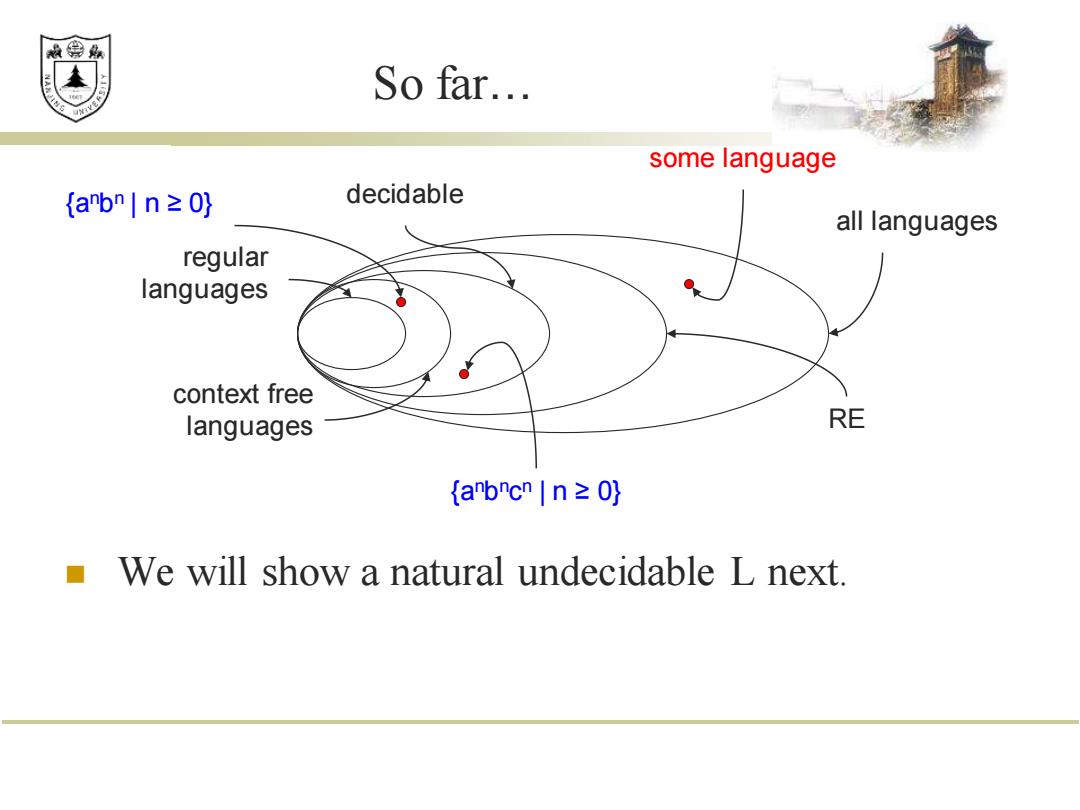
So far… ◼ We will show a natural undecidable L next. regular languages context free languages all languages decidable RE {a nb n | n ≥ 0} {a nb nc n | n ≥ 0} some language

效绵鼎 The Halting Problem Definition of the“Halting Problem”: HALT ={<M,x>TM M halts on input x ■Is HALT decidable?
The Halting Problem ◼ Definition of the “Halting Problem” : HALT = { <M, x> | TM M halts on input x } ◼ Is HALT decidable?

效绵鼎 The Halting Problem Theorem:HALT is not decidable (undecidable). Proof: o Suppose TM H decides HALT if M halts on x,H accept if M does not halt on x,H reject o Define new TM H':on input <M> if H accepts <M,<M>>,then loop if H rejects <M,<M>>,then halt consider H'on input <H'>: if it halts,then H rejects <H',<H'>>,which implies it cannot halt if it loops,then H accepts <H',<H'>>,which implies it must halt contradiction.Thus neither H nor H'can exist
The Halting Problem Theorem: HALT is not decidable (undecidable). Proof: Suppose TM H decides HALT ◼ if M halts on x, H accept ◼ if M does not halt on x, H reject Define new TM H’: on input <M> ◼ if H accepts <M, <M>>, then loop ◼ if H rejects <M, <M>>, then halt consider H’ on input <H’>: ◼ if it halts, then H rejects <H’, <H’>>, which implies it cannot halt ◼ if it loops, then H accepts <H’, <H’>>, which implies it must halt contradiction. Thus neither H nor H’ can exist

效绵鼎 Where's the Diagonalization? Entry ij is the value of H on input <Mi,<M> A=Accept,R=Reject <M1><M2><M3><M4> MI A R A R M2 A A A A M3 R R R R M4 A A R R
Where’s the Diagonalization? ◼ Entry i,j is the value of H on input <Mi , <Mj>> <M1> <M2> <M3> <M4> … M1 A R A R M2 A A A A M3 R R R R M4 A A R R … A = Accept, R = Reject

戏绵鼎 H'is the opposite of the diagonals Entry i,j is the value of H on input <Mi,<M> <M1><M2><M3><M4>..<H'> MI A R A R M2 A A A A M3 R R R R M4 A A R R H R R A A ?
H’ is the opposite of the diagonals: ◼ Entry i,j is the value of H on input <Mi , <Mj>> <M1> <M2> <M3> <M4> … <H’> M1 A R A R M2 A A A A M3 R R R R M4 A A R R … H’ R R A A ?