有向图的邻接表和逆邻接表 data adi dest link A 0 A dest link 1 B 0 2 B 2 C 邻接表(出边表) C data adj dest link A 1 B 2 C 逆邻接表(入边表) 26
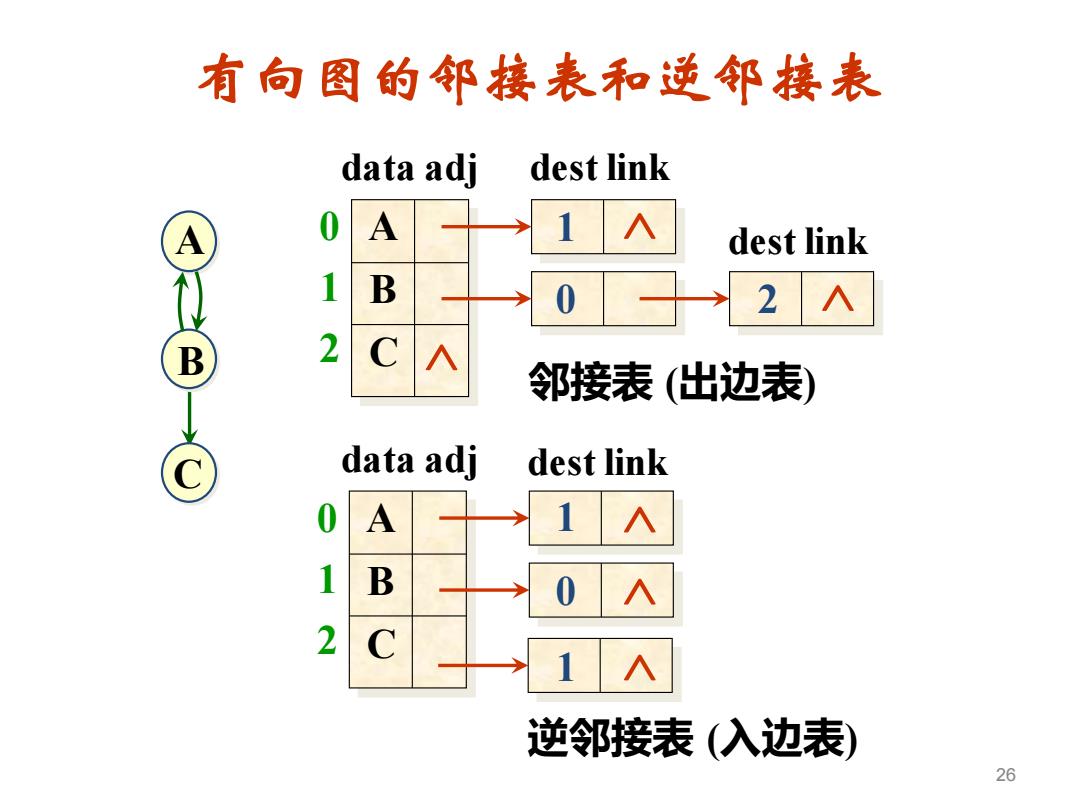
有向图的邻接表和逆邻接表 26 data adj A B C 0 1 2 dest link dest link 邻接表 (出边表) data adj A B C 0 1 2 dest link 逆邻接表 (入边表) 1 0 2 0 1 1 A B C
网络(带权图)的邻接表 data adj dest cost link A >15→36Λ 28 2 32 3 1 顶点表) (出边表) 统计出边表中结点个数,得到该顶点的出度; ·统计入边表中结点个数,得到该顶点的入度。 27
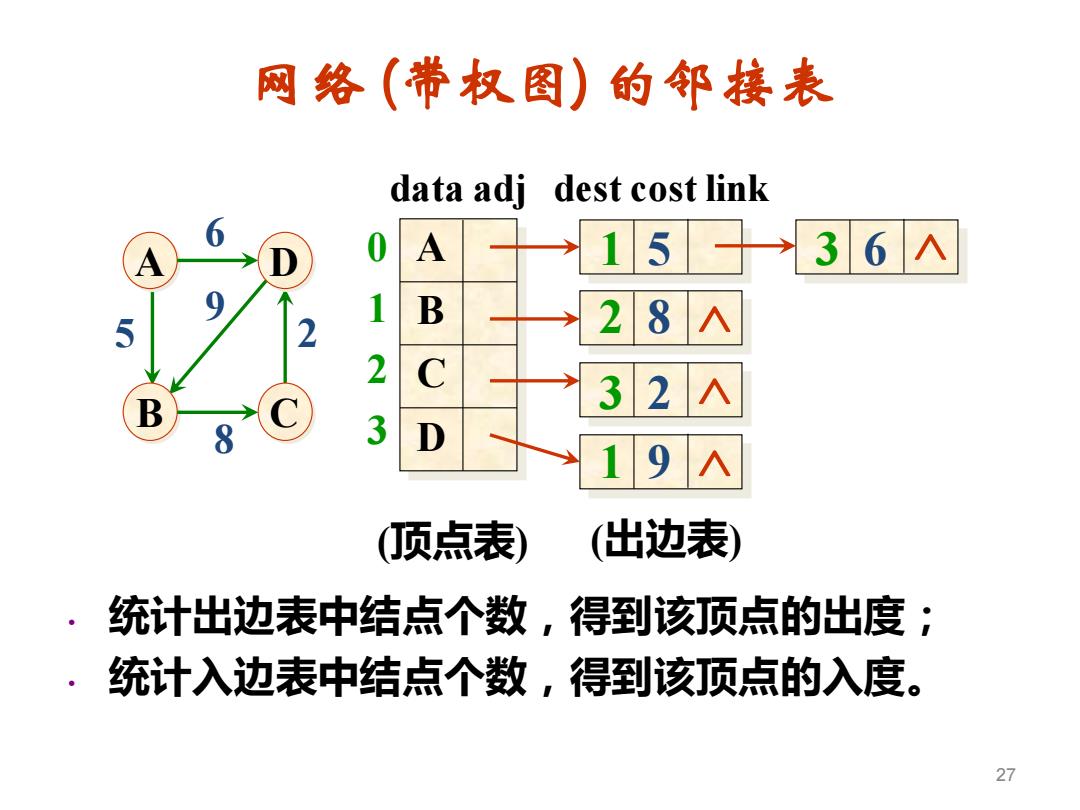
网络 (带权图) 的邻接表 • 统计出边表中结点个数,得到该顶点的出度; • 统计入边表中结点个数,得到该顶点的入度。 27 B A C D 6 9 5 2 8 data adj A B C D 0 1 2 3 dest cost link 1 5 3 6 2 8 3 2 1 9 (顶点表) (出边表)

用邻接表表示的图的类定义 template <class T,class E> struct Edge 川边结点的定义 int dest; 川边的另一顶点位置 E cost; /川边上的权值 Edge<T,E>*link; /下一条边链指针 Edge ( /构造函数 Edge (int num,E c) /构造函数 dest (num),cost (c),link (NULL) bool operator!=(Edge<T,E>&R)const {return dest!=R.dest?true:false;}l/判边等否 }; 28
用邻接表表示的图的类定义 template <class T, class E> struct Edge { //边结点的定义 int dest; //边的另一顶点位置 E cost; //边上的权值 Edge<T, E> *link; //下一条边链指针 Edge () {} //构造函数 Edge (int num, E c) //构造函数 : dest (num), cost (c), link (NULL) { } bool operator != (Edge<T, E>& R) const { return dest != R.dest ? true:false; } //判边等否 }; 28

template <class T,class E> struct Vertex 川顶点的定义 T data; /顶点的名字 Edge<T,E>*adj; /川边链表的头指针 }; template <class T,class E> class Graphlnk:public Graph<T,E>{/图的 类定义 friend istream&operator >(istream&in, Graphlnk<T,E>&G); /输入 friend ostream&operator <(ostream&out, Graphlnk<T,E>&G); /输出 29
template <class T, class E> struct Vertex { //顶点的定义 T data; //顶点的名字 Edge<T, E> *adj; //边链表的头指针 }; template <class T, class E> class Graphlnk : public Graph<T, E> { //图的 类定义 friend istream& operator >> (istream& in, Graphlnk<T, E>& G); //输入 friend ostream& operator << (ostream& out, Graphlnk<T, E>& G); //输出 29

private: Vertex<T,E>*Node Table; /顶点表(各边连表的头结点) int get VertexPos (const T vertex) /给出顶点vertex在图中的位置 for (int i=0;i<num Vertices;i+) if (NodeTablei].data =vertex)return i; return -1; public: Graphlnk(int sz=Default Vertices);/构造函 数 GraphlnkO; /析构数 30
private: Vertex<T, E> *NodeTable; //顶点表 (各边链表的头结点) int getVertexPos (const T vertex) { //给出顶点vertex在图中的位置 for (int i = 0; i < numVertices; i++) if (NodeTable[i].data == vertex) return i; return -1; } public: Graphlnk (int sz = DefaultVertices); //构造函 数 ~Graphlnk(); //析构函数 30