
第五章树 树和森林的概念 二叉树 二叉树遍历 线索化二叉树 树与森林 堆 Huffman树 1
第五章 树 • 树和森林的概念 • 二叉树 • 二叉树遍历 • 线索化二叉树 • 树与森林 • 堆• Huffman树 1

树和森林的概念 ·有根树: ◆一棵有根树T,简称为树,它是n(n≥0)个结点 的有限集合。当n=0时,T称为空树:否则,T 是非空树。记作 n=0 fI,T,Tar,Tm,n>0 ◆r是一个特定的称为根(roo)的结点,它只有直 接后继,没有直接前驱 ◆根以外的其他结点划分为m(m≥0)个互不相交 的有限集合T1,T2,,Tm,每个集合又是一棵树, 并且称为根的子树 2
树和森林的概念 • 有根树: ◆ 一棵有根树T,简称为树,它是n (n ≥ 0) 个结点 的有限集合。当n = 0时,T 称为空树;否则,T 是非空树。记作 ◆ r 是一个特定的称为根 (root) 的结点,它只有直 接后继,没有直接前驱 ◆ 根以外的其他结点划分为 m (m 0) 个互不相交 的有限集合T1 , T2 , …, Tm,每个集合又是一棵树, 并且称为根的子树 = = 0 0 r,T ,T ,...,T , n , n T 1 2 m { } Φ 2
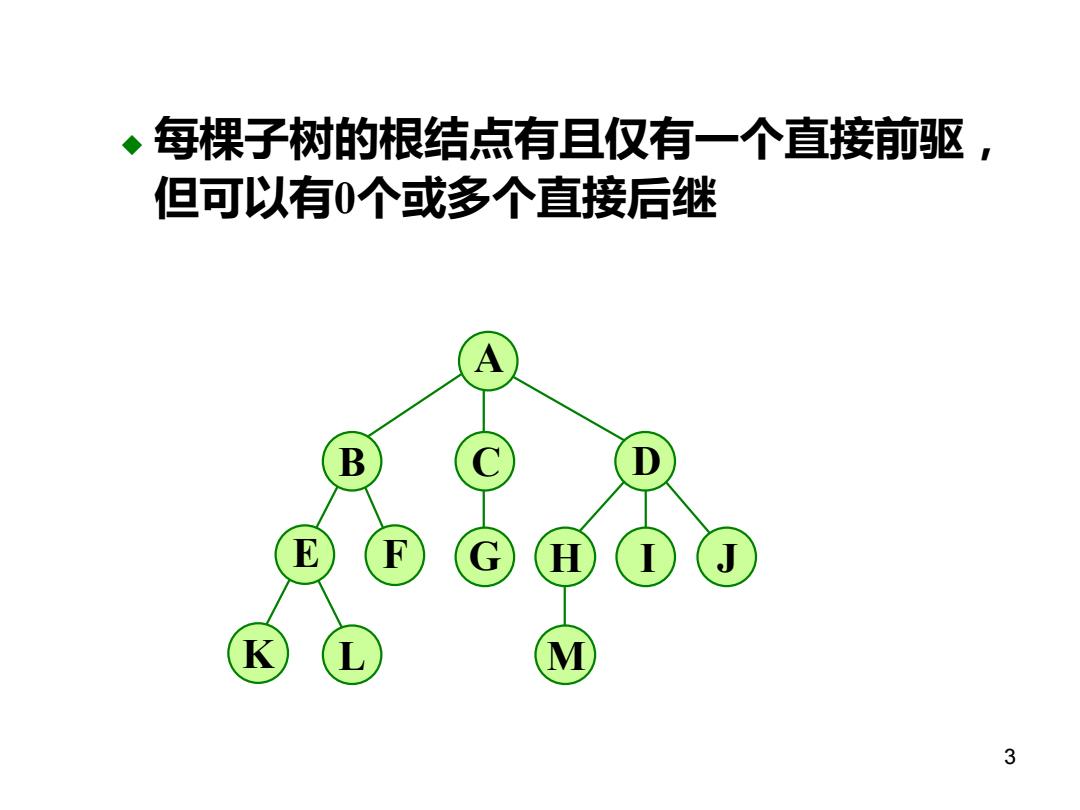
每棵子树的根结点有且仅有一个直接前驱, 但可以有0个或多个直接后继 A B D E F G H J K M 3
◆ 每棵子树的根结点有且仅有一个直接前驱, 但可以有0个或多个直接后继 3 D A B C E F G H I J K L M

树的基本术语 ·子女:若结点的子树非空,结点子树的根即 为该结点的子女。 .双亲(父亲):若结点有子女,该结点是子 女的双亲(父亲)。 兄弟:同一结点的子女互称为兄弟。 . 度:结点的子女个数即为该结点的度;树中 各个结点的度的最大值称为树的度。 4
树的基本术语 • 子女:若结点的子树非空,结点子树的根即 为该结点的子女。 • 双亲(父亲):若结点有子女,该结点是子 女的双亲(父亲)。 • 兄弟:同一结点的子女互称为兄弟。 • 度:结点的子女个数即为该结点的度;树中 各个结点的度的最大值称为树的度。 4

分支结点:度不为0的结点即为分支结点, 亦称为非终端结点。 叶结点:度为0的结点即为叶结点,亦称为 终端结点。 祖先:根结点到该结点的路径上的各个结点 都是该结点的祖先。 ·子孙:某结点的所有下属结点,都是该结点 的子孙。 5
• 分支结点:度不为0的结点即为分支结点, 亦称为非终端结点。 • 叶结点:度为0的结点即为叶结点,亦称为 终端结点。 • 祖先:根结点到该结点的路径上的各个结点 都是该结点的祖先。 • 子孙:某结点的所有下属结点,都是该结点 的子孙。 5