
第八章 图 图的基本概念 图的存储结构 图的遍历与连通性 最小生成树 最短路径 活动网络 1
第八章 图 • 图的基本概念 • 图的存储结构 • 图的遍历与连通性 • 最小生成树 • 最短路径 • 活动网络 1

图的基本概念 图定义图是由顶点vertex)集合以及顶点 之间的关系集合组成的一种数据结构: G=(E) 其中V={xx∈某个数据对象} 是顶点的有穷非空集合: E={c,y)x,y∈V 或E={x,Jy>|x,Jy∈V&&Pth(化,y)} 是顶点之间关系的有穷集合,也叫做边 (edge)集合。Path (x,y)表示从x到y的一 条单向通路,它是有方向的。 2
图的基本概念 • 图定义 图是由顶点(vertex)集合以及顶点 之间的关系集合组成的一种数据结构: G=( V, E ) 其中 V = { x | x 某个数据对象} 是顶点的有穷非空集合; E = {(x, y) | x, y V } 或 E = {<x, y> | x, y V && Path (x, y)} 是顶点之间关系的有穷集合,也叫做边 (edge)集合。Path (x, y)表示从 x 到 y 的一 条单向通路, 它是有方向的。 2
有向图与无向图; 在有向图中,顶点对<x, y>是有序的。在无向图中,顶点对(x,y)是 无序的。 完全图若有n个顶点的无向图有nn-1)/2 条边,则此图为无向完全图。若有n个顶点 的有向图有nn-)条边,则此图为有向完全 图。 0 1 2 2 3
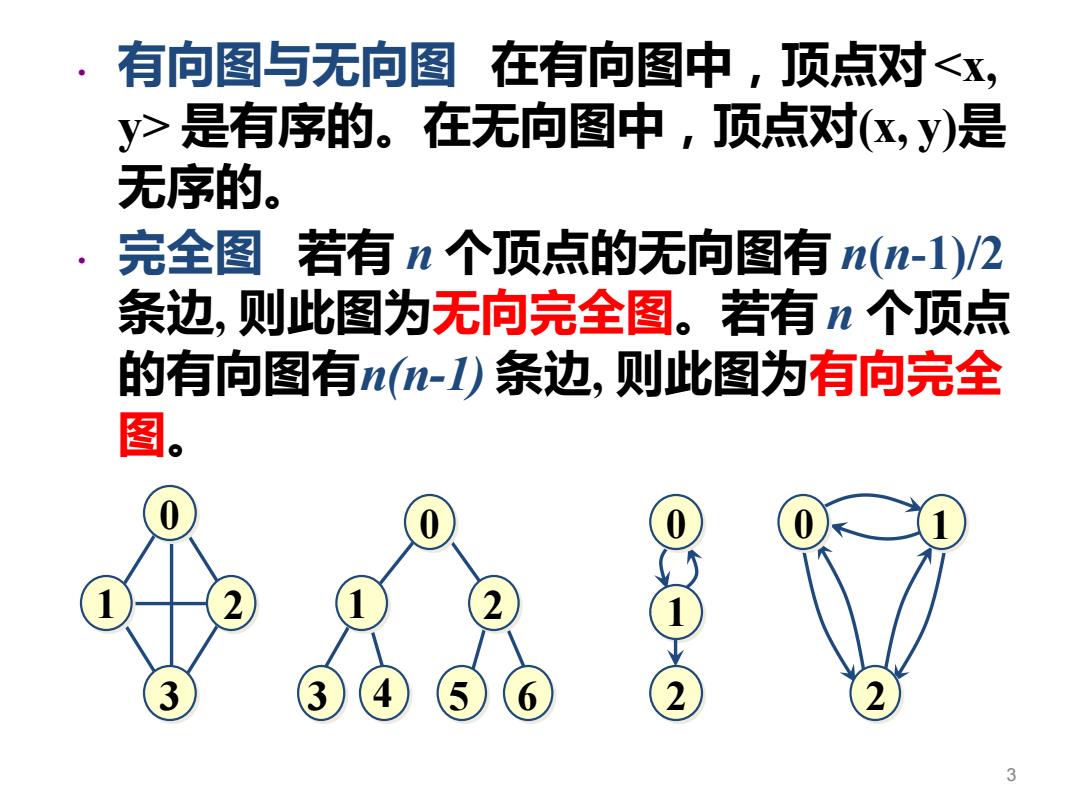
• 有向图与无向图 在有向图中,顶点对<x, y> 是有序的。在无向图中,顶点对(x, y)是 无序的。 • 完全图 若有 n 个顶点的无向图有 n(n-1)/2 条边, 则此图为无向完全图。若有n 个顶点 的有向图有n(n-1) 条边, 则此图为有向完全 图。 3 0 0 0 0 1 1 1 2 1 2 3 3 4 5 6 2 2
邻接顶点 如果(w,y)是E(G)中的一条边, 则称u与v互为邻接顶点。 子图设有两个图G=(V,E)和G=(八,E)。 若V'sV且EcE,则称图G'是图G的子图。 子图 2 2 2 .权或权重(weigh)在某些图中,边具有与 它相关的数值,称为权重。带权图也叫作网 络(network)。 4
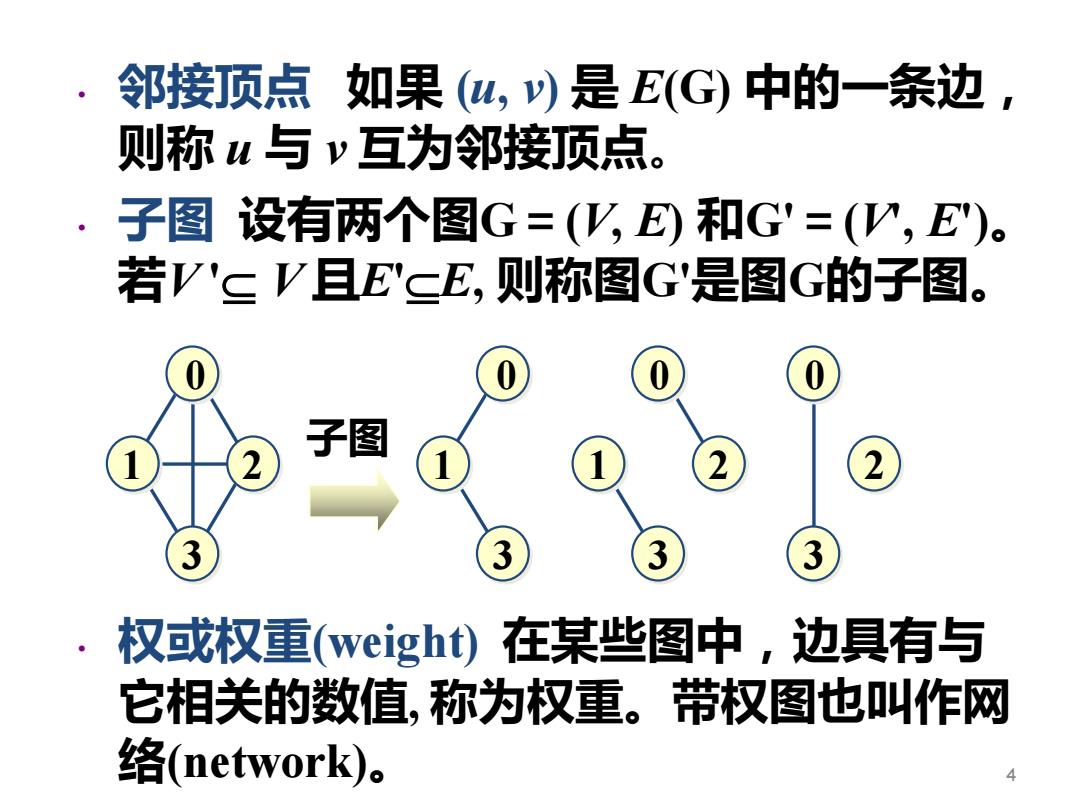
• 邻接顶点 如果 (u, v) 是 E(G) 中的一条边, 则称 u 与 v 互为邻接顶点。 • 子图 设有两个图G=(V, E) 和G'=(V', E')。 若V ' V 且E'E, 则称图G'是图G的子图。 • 权或权重(weight) 在某些图中,边具有与 它相关的数值, 称为权重。带权图也叫作网 络(network)。 4 子图 0 1 2 3 0 1 3 0 1 2 3 0 2 3

J顶点的度(degree) 一个顶点的度是与它相关联 的边的条数,记作deg(y)。 。 在有向图中,顶点v的入度是以v为终点的有向边 的条数,记作indeg(少;顶点v的出度是以v为始 点的有向边的条数,记作outdeg(y)。在有向图中, 顶点的度等于该顶点的入度与出度之和。 路径 在图G=(V,E)中,若从顶点y:出发,沿一 些边经过若干顶点%1,2,,pm,到达顶点, 则称顶点序列(,p1,p2,…,m,》为从顶点 到顶点y的一条路径。它经过的边(y%”1小、(, y2以小、、(ypm)都是来自于E的边。 5
• 顶点的度 (degree) 一个顶点v的度是与它相关联 的边的条数, 记作deg(v)。 • 在有向图中, 顶点 v 的入度是以 v 为终点的有向边 的条数, 记作 indeg(v); 顶点 v 的出度是以 v 为始 点的有向边的条数, 记作 outdeg(v)。在有向图中, 顶点的度等于该顶点的入度与出度之和。 • 路径 在图 G=(V, E) 中, 若从顶点 vi出发, 沿一 些边经过若干顶点 vp1 , vp2 , …, vpm,到达顶点vj, 则称顶点序列 (vi , vp1 , vp2 , ... , vpm , vj ) 为从顶点vi 到顶点 vj 的一条路径。它经过的边(vi , vp1 )、(vp1 , vp2 )、...、(vpm, vj ) 都是来自于E的边。 5