
2、伯努利方程 数学表述: P+Pgh+2m2=常数 物理表述: 同一流线,能量密度之和守恒 适用条件: (1)理想流体 (2)定常流动 (3)同一流线
2、伯努利方程 适用条件: (1)理想流体 (2)定常流动 (3)同一流线 + + 2 =常数 2 1 数学表述: P gh v 物理表述: 同一流线,能量密度之和守恒
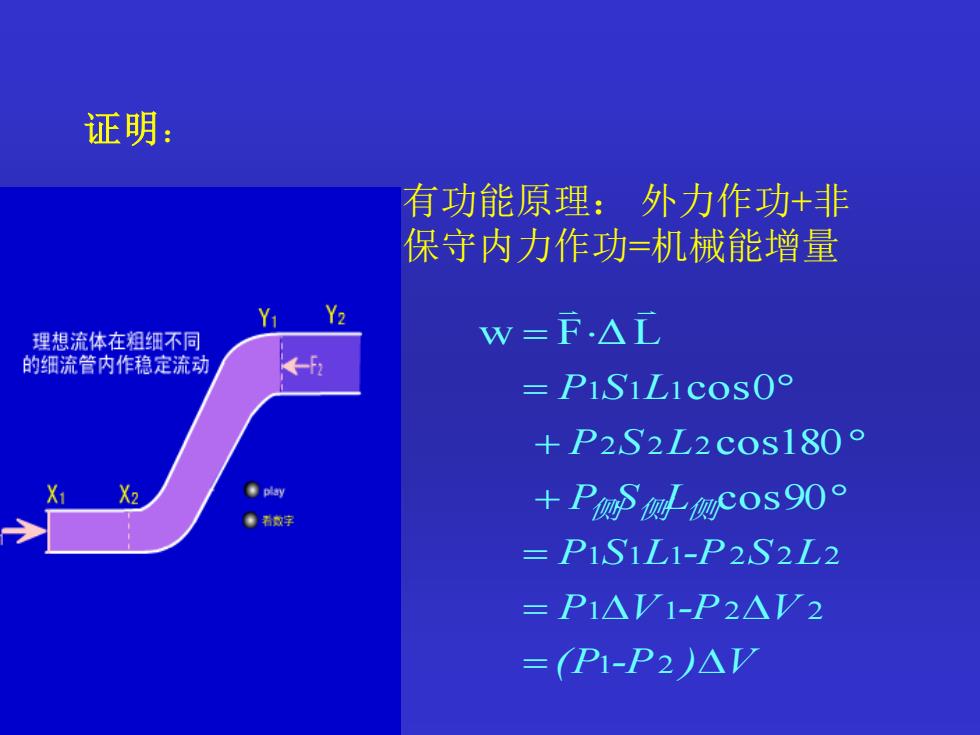
证明: 有功能原理:外力作功+非 保守内力作功=机械能增量 Y Y2 理想流体在粗细不同 w=F△ 的细流管内作稳定流动 ←f =P1S1Licos0 +P2S2L2cos180° ● ●看数字 +PRScos90 =P1S1L1-P2S2L2 =P1△V1-P2△V2 =P1-P2)△☑
证明 : 有功能原理: 外力作功 + 非 保守内力作功 =机械能增量 ( P -P ) V P V -P V P S L -P S L P S L P S L P S L 侧 侧 侧 = = =+ + = = 1 2 1 1 2 2 1 1 1 2 2 2 2 2 2 1 1 1 cos90 cos180 cos 0 w F Δ L

机械能增量: △E=E+E2)-(E+E2 =E3-E1 =(△mi+△mgh:》 (△m+△mgh) 根据功能原理:W=E
机械能增量: -( mv mgh ) ( mv mgh ) E -E E ( E E )-(E E ) 1 2 1 2 2 2 2 1 2 1 3 1 3 2 1 2 + = + = = + + 根据功能原理:W=ΔE

(RAngshAmmgh 等式两边同除△y利用P=会有 月-月-5m:2+g-2m2-g% 移项:R+Pm+P8h=B+2,+Pgh 由于1点、2点的任意性,可得到伯努力方程 P+P+gh=常数
1 2 2 1 2 1 2 2 2 1 2 1 ( P − P )V = mv +mgh − mv −mgh 1 2 2 1 2 1 2 2 2 1 2 1 P −P = v + gh − v − gh 移项: 2 2 1 2 2 2 1 1 2 1 2 1 P + v + gh = P + v + gh 由于1点、2点的任意性,可得到伯努力方程 V 利用 V m 等式两边同除 = 有 P+ V 2 + gh =常数 2 1

其中: P一压强能密度 动能密度 P3h一重力势能密度 ,能量密度之和不变 证毕!
其中: P — 压强能密度 2 2 1 v — 动能密度 gh — 重力势能密度 ∴能量密度之和不变 证毕!