吉林大学：《医用物理学》课程电子教案（PPT课件）第二章 血液的流动

例：水在下图装置内做定常流动。若压强计用水银做测量液体 求：P1P2=?(忽略1点与2点的高度差) 水流 解：当定常流动时，U形压强 计中的流体是静止的，符 合静压强的有关规律。 P:=P P3=P1+pxgh+pxgAh P,P+Pgh+P怒h p水=10kgm 联立求解得： P-P2(p银P水）g4h P银13.6X103kgm 即：P银>P水 ≈p8h

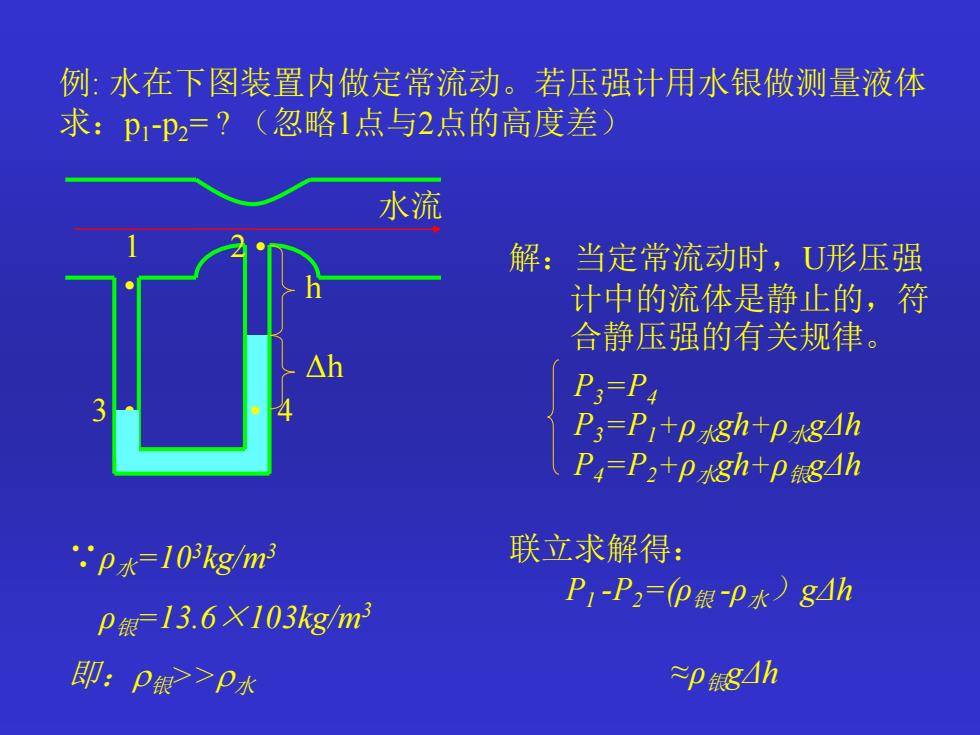
例: 水在下图装置内做定常流动。若压强计用水银做测量液体 求：p1 -p2= ? （忽略1点与2点的高度差） 解：当定常流动时，U形压强 计中的流体是静止的，符 合静压强的有关规律。 ∵ρ水=103kg/m3 ρ银=13.6×103kg/m3 即：银>>水 P3=P4 P3=P1+ρ水gh+ρ水gΔh P4=P2+ρ水gh+ρ银gΔh 联立求解得： P1 -P2=(ρ银 -ρ水）gΔh ≈ρ银gΔh 水流 1 2 • • 3 • • 4 h Δh

2 水流 P1-P2p水gAh 水流 Ah P银 水流 P1-P2P水gAh P1-P2P银gAh

P1 – P2=ρ水gΔh P1 – P2=ρ水gΔh P1 – P2=ρ银gΔh h 1 • 2 • 水流 1 • 水流 2 • Δh 1 ρ银 • 2 • Δh 水流

二、运动规律 1、连续性原理 (Contiunity Equation) 数学表述： Sv=常数 物理表述： 同一流管流量守恒。 适用条件： (1)不可压缩流体 (2)定常流动 (3)在同一流管

二、运动规律 适用条件： （1）不可压缩流体 （2）定常流动 （3）在同一流管 1、连续性原理（Contiunity Equation） 数学表述： S=常数 物理表述： 同一流管流量守恒

证明： 流进流管的体积=流出流管的体积 △V=△V2 (不可压缩性) S1V1△t=S2V2△t 理想流体在粗细不同 的细流管内作稳定流动 ←f2 .SIVI=S2V2 1点与2点是任选的，则 ●ply Sv=常数 ●看数字 若流管中某截面上的流速不是定 值，则速度应用平均值： Sv=常数 证毕！

证明： ΔV1=ΔV2 （不可压缩性） S11Δt=S22 Δt ∴ S11=S22 1点与2点是任选的，则 S =常数 流进流管的体积=流出流管的体积 若流管中某截面上的流速不是定 值，则速度应用平均值： Sv =常数 证毕！

例：请你列出下面2种流管分布的连续性原理方程 SV=S2V2 S2变小V变大 SVI=S2V2+S3V3+S4V4 截面积小的地方流速大

例：请你列出下面2种流管分布的连续性原理方程 S11=S22 S2 变小  2变大 S11=S22+S33+S44 1 • • 2 1• 2 • 3 • 4 • 截面积小的地方流速大