十进制异步减法计数器 /0 /0/0 10 排列顺序: 0000←-0001-0010←-0011←-0100 态图 0:0"0"O3 /1↓ ↑/0 1001→1000→0111→0110→0101 0 10 /0 /0 选用4个CP上升沿触发 02' 的JK触发器,分别用FFo、 2"2 00 01 11 10 FF1、FF2、FF3表示。 00 0 0 输出方程: 01 0 0 × 0 B=Q"⑨"g"⑨" 11 0 0 10 0 0 X B的卡诺图
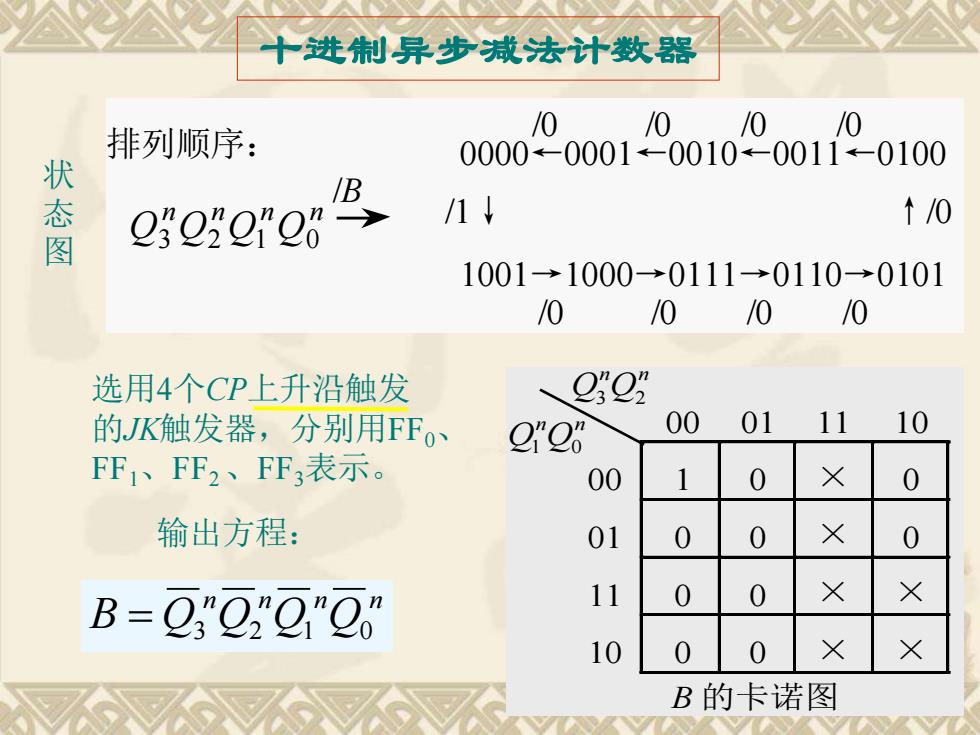
十进制异步减法计数器 选用4个CP上升沿触发 的JK触发器,分别用FF0、 FF1、FF2 、FF3表示。 /0 /0 /0 /0 0000←0001←0010←0011←0100 /1↓ ↑/0 1001→1000→0111→0110→0101 /0 /0 /0 /0 排列顺序: /B n n n n Q3 Q2 Q1 Q0 状 态 图 输出方程: n n n n B = Q3 Q2 Q1 Q0 B 的卡诺图 00 01 11 10 00 1 0 × 0 01 0 0 × 0 11 0 0 × × 10 0 0 × × n n Q3 Q2 n n Q1 Q0

CP 时序图 4 2 选择时钟脉冲的一个基本原则:在满足 翻转要求的条件下,触发沿越少越好。 时 FF,每输入一个CP翻转一次,只能选CP。 CP =CP 钟 FF,在t2、t4、t6、g时刻翻转,可选Qo。 CP=C0 FF2在t4、t时刻翻转,可选Q1。 程 FF3在tg、to时刻翻转,可选Q0。 CP=Q
CP Q0 Q1 Q2 Q3 t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 1 0 时 序 图 时 钟 方 程 CP0 = CP CP1 = Q0 CP2 = Q1 FF0每输入一个CP翻转一次,只能选CP。 选择时钟脉冲的一个基本原则:在满足 翻转要求的条件下,触发沿越少越好。 FF1在t2、t4、t6、t8时刻翻转,可选Q0。 FF2在t4、t8时刻翻转,可选Q1。 FF3在t8、t10时刻翻转,可选Q0。 CP3 = Q0
t10 44 OO: 2"26 00 01 10 状态方程 00 01 O"=0r0"0"O" 11 O=0" 10 Q+1=2"0"g1 (d) Q的卡诺图
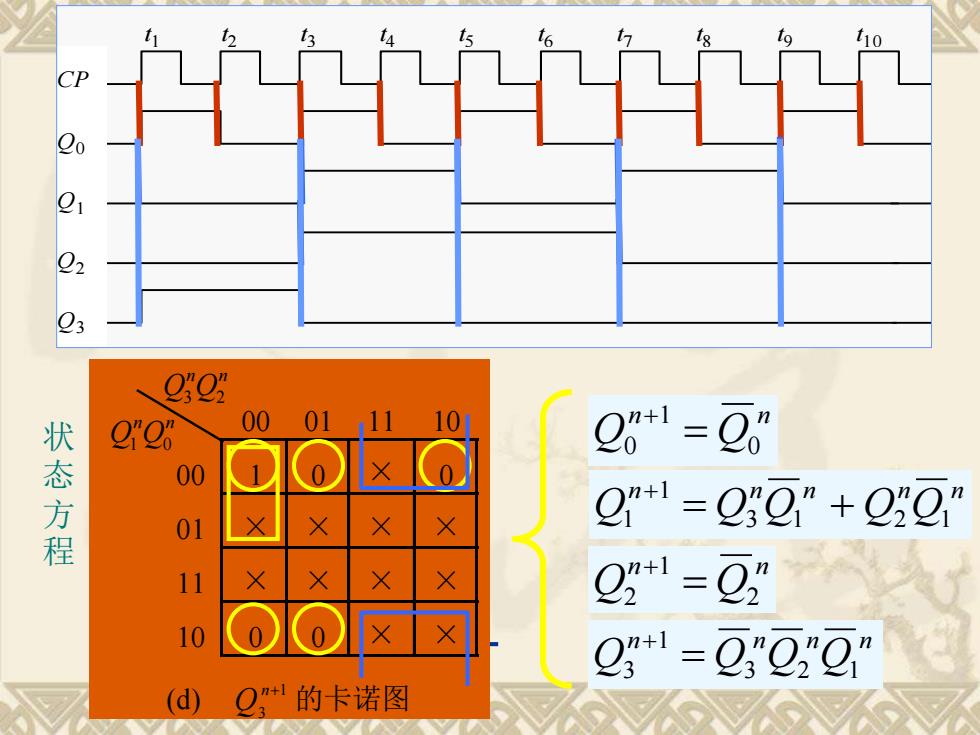
CPQ0 Q1 Q2 Q3 t1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 1 0 (a) 1 0n + Q 的卡诺图 00 01 11 10 00 1 1 × 1 01 0 0 × 0 11 0 0 × × 10 1 1 × × n n Q3 Q2 n n 状 Q1 Q0 态方程 n n Q Q0 1 0 = + (b) 1 1n + Q 的卡诺图 00 01 11 10 00 0 1 × 1 01 × × × × 11 × × × × 10 0 0 × × n n Q3 Q2 n n Q1 Q0 n n n n n Q Q3 Q1 Q2 Q1 1 1 = + + 00 01 11 10 00 × 0 × 1 01 × × × × 11 × × × × 10 × × × × n n Q3 Q2 n n Q1 Q0 (c) 1 2n + Q 的卡诺图 n n Q Q2 1 2 = + 00 01 11 10 00 1 0 × 0 01 × × × × 11 × × × × 10 0 0 × × n n Q3 Q2 n n Q1 Q0 (d) 1 3n + Q 的卡诺图 n n n n Q Q3 Q2 Q1 1 3 = +
Q+=19”+1·Q6 比较,得驱动纺程: 2"+1=(Q+Q2)·g”+1·Q” J0=K0=1 Q2+1=10”+1·Q J1=Q3+Q,K=1 Q1=Q"g”.Q”+1·Q J2=K2=1 Q+1=J0”+KQ” J3=0"⑨”,K3=1 电路图 S7 FFo FF FF2 FF3 & 1J B & 将无效状态1010~1111分别代入状态方程进行计算,可以验证 在CP脉冲作用下都能回到有效状态,电路能够自启动
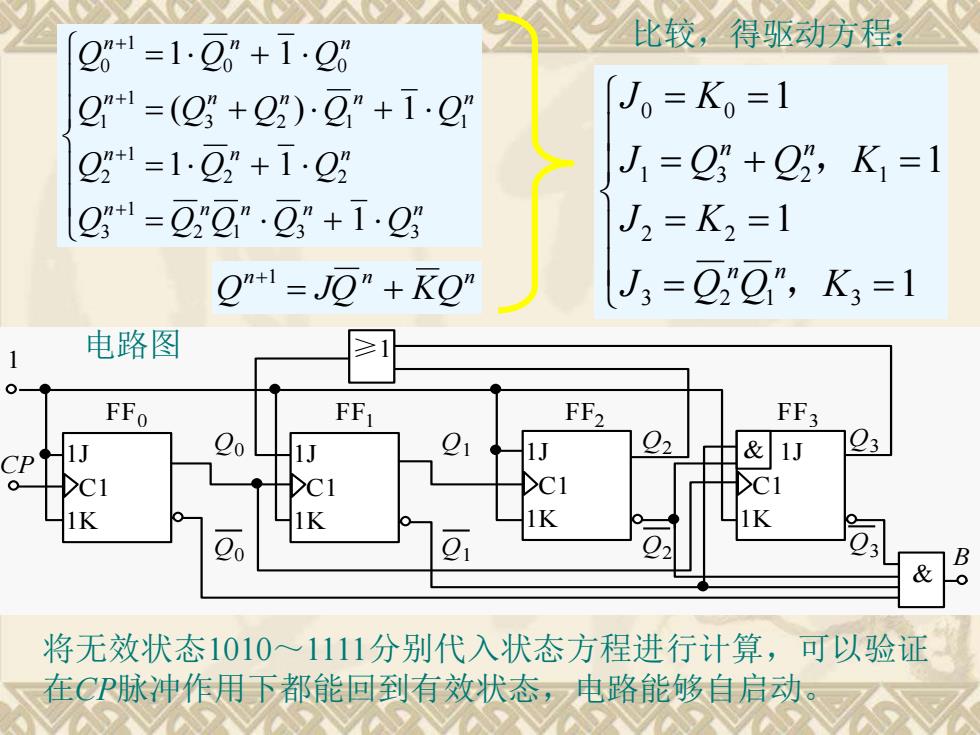
Q0 Q0 B F F0 FF1 FF2 F F3 Q2 Q2 Q1 Q1 Q3 Q3 1J C1 1K 1J C1 1K & CP 1J & C1 1K 1J C1 1K ≥1 1 比较,得驱动方程: 电路图 将无效状态1010~1111分别代入状态方程进行计算,可以验证 在CP脉冲作用下都能回到有效状态,电路能够自启动。 = = = = = + = = = 1 1 1 1 3 2 1 3 2 2 1 3 2 1 0 0 J Q Q K J K J Q Q K J K n n n n , , = + = + = + + = + + + + + n n n n n n n n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 2 1 3 3 1 3 2 2 1 2 3 2 1 1 1 1 0 0 1 0 1 1 1 ( ) 1 1 1 n n n Q = JQ + KQ +1
CPo NC 2o 03 GND 122 Co 03 21 02 999991 9 9 14 131211109 8 成十进 CPo 74LS90 74LS90 CP 2 3 45 制 CPI ROA ROB NC VCC SOA SOB SOA SOB ROA RoB (a) 引脚排列图 (b) 逻辑功能示意图 异步计数器45 输 入 输 出 RoA RoB SoB CPo CP Q"+ Q"1Q+1Qg+ 1 1 0 × × 0 0 0 0(清零) 1 1 0 × × 0 0 0(清零) × 1 × X 0 0 1(置9) × 0 0 ↓ 0 二进制计数 0 0 五进制计数 0 0 90 20 8421码十进制计数 0 × ↓ 5421码十进制计数
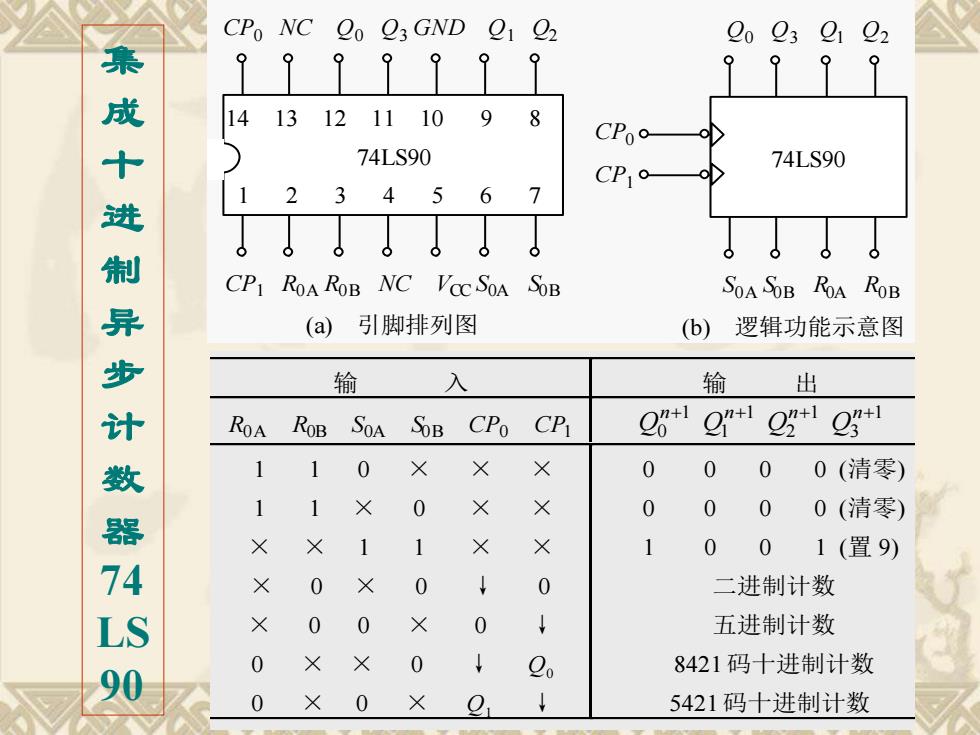
CP1 R0 A R0B NC VCC S0A S0 B 14 13 12 11 10 9 8 74LS90 1 2 3 4 5 6 7 CP0 NC Q0 Q3 GND Q1 Q2 74LS90 S0A S0B R0A R0 B Q0 Q 3 Q1 Q 2 CP0 CP1 (a) 引脚排列图 (b) 逻辑功能示意图 集成十进制异步计数器 74 LS 90 输 入 输 出 R0 A R0B S0A S0 B CP0 CP1 1 3 1 2 1 1 1 0 n+ n+ n+ n + Q Q Q Q 1 1 0 × × × 1 1 × 0 × × × × 1 1 × × × 0 × 0 ↓ 0 × 0 0 × 0 ↓ 0 × × 0 ↓ Q 0 0 × 0 × Q1 ↓ 0 0 0 0 (清零) 0 0 0 0 (清零) 1 0 0 1 ( 置 9) 二进制计数 五进制计数 8421 码十进制计数 5421 码十进制计数