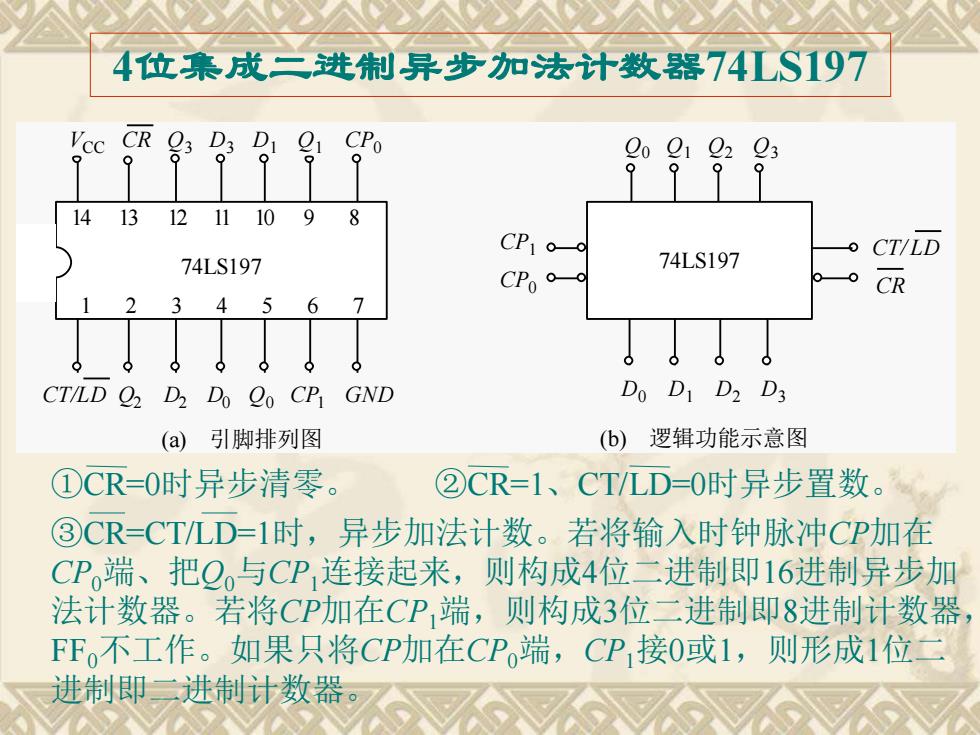
4位集成二进制异步加法计数器74LS197 VcC CR 23 D3 D1 1 CPo C0 01 02 03 141312111098 。CT/LD 74LS197 74LS197 CPo 0 CR 2 3 4 6 CT/LD Q2 D2 Do Qo CP GND Do D D2 D3 (a)引脚排列图 (b)逻辑功能示意图 ①CR=O时异步清零。 ②CR=1、CT/LD=O时异步置数。 ③CR=CTLD=1时,异步加法计数。若将输入时钟脉冲CP加在 CP端、把Q,与CP连接起来,则构成4位二进制即16进制异步加 法计数器。若将CP加在CP端,则构成3位二进制即8进制计数器 FFo不工作。如果只将CP加在CP端,CP接0或1,则形成1位二 进制即三进制计数器
4位集成二进制异步加法计数器74LS197 CP1 CP0 74LS197 Q0 Q1 Q2 Q3 (a) 引脚排列图 (b) 逻辑功能示意图 14 13 12 11 10 9 8 74LS197 1 2 3 4 5 6 7 VCC CR Q3 D3 D1 Q1 CP0 CT/L D Q2 D2 D0 Q0 CP1 GND D0 D1 D2 D3 CT/L D CR ①CR=0时异步清零。 ②CR=1、CT/LD=0时异步置数。 ③CR=CT/LD=1时,异步加法计数。若将输入时钟脉冲CP加在 CP0端、把Q0与CP1连接起来,则构成4位二进制即16进制异步加 法计数器。若将CP加在CP1端,则构成3位二进制即8进制计数器, FF0不工作。如果只将CP加在CP0端,CP1接0或1,则形成1位二 进制即二进制计数器

2、异步十进制计数器 十进制异步加法计数器 /010 /0/0 排列顺序: 00000001→0010→0011-→0100 态 Q3'QQ”Q8 /1↑ ↓/0 1001←1000←-0111←-0110←-0101 10 /10 /0 /0 OO" 选用4个CP上升沿触发 的D触发器,分别用FFo Q"O' 00 01 11 10 00 0 0 FF1、FF2、FF3表示。 0 0 输出方程: 01 11 0 0 × × C=Q06 10 0 0 × × C的卡诺图
选用4个CP上升沿触发 的D触发器,分别用FF0、 FF1、FF2 、FF3表示。 0000→0001→0010→0011→0100 /1↑ ↓/0 1001←1000←0111←0110←0101 /0 /0 /0 /0 /0 /0 /0 /0 排列顺序: /C n n n n Q3 Q2 Q1 Q0 2、异步十进制计数器 状 态 图 输出方程: n n C = Q3 Q0 C 的卡诺图 00 01 11 10 00 0 0 × 0 01 0 0 × 1 11 0 0 × × 10 0 0 × × n n Q3 Q2 n n Q1 Q0 十进制异步加法计数器
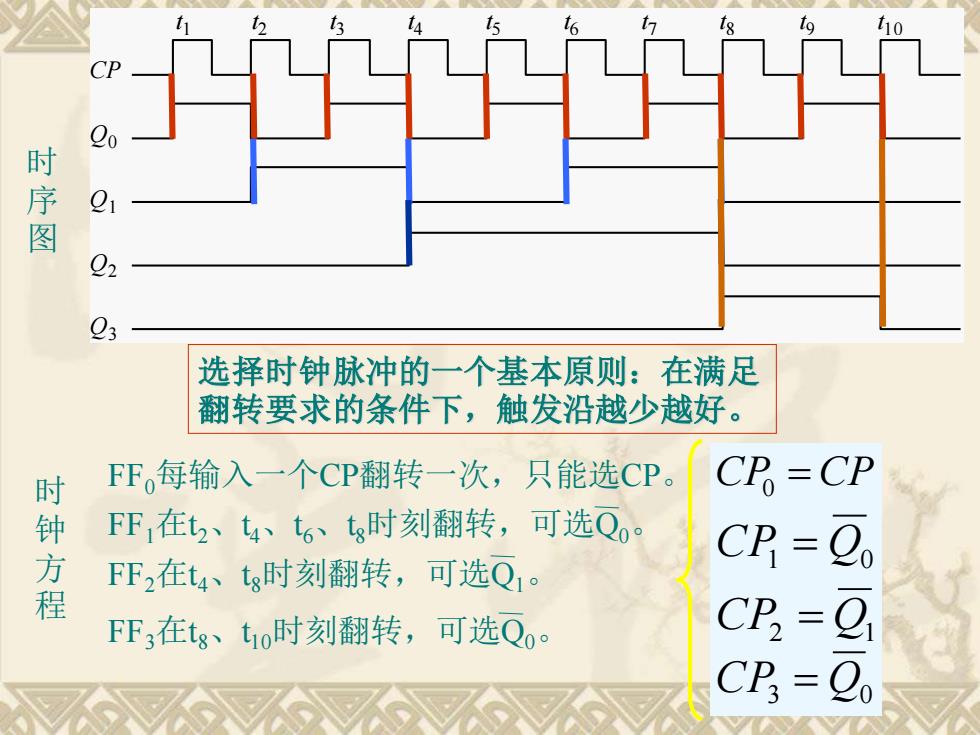
10 时序图 93 选择时钟脉冲的一个基本原则:在满足 翻转要求的条件下,触发沿越少越好。 时 FF,每输入一个CP翻转一次,只能选CP。 C =CP FF1在2、t4、t6、g时刻翻转,可选Qo FF2在t4、tg时刻翻转,可选Q1。 CP =Q 方程 FF3在tg、to时刻翻转,可选Qo。 = CP =
CP Q0 Q1 Q2 Q3 t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 1 0 时 序 图 时 钟 方 程 CP0 = CP CP1 = Q0 CP2 = Q1 FF0每输入一个CP翻转一次,只能选CP。 选择时钟脉冲的一个基本原则:在满足 翻转要求的条件下,触发沿越少越好。 FF1在t2、t4、t6、t8时刻翻转,可选Q0。 FF2在t4、t8时刻翻转,可选Q1。 FF3在t8、t10时刻翻转,可选Q0。 CP3 = Q0
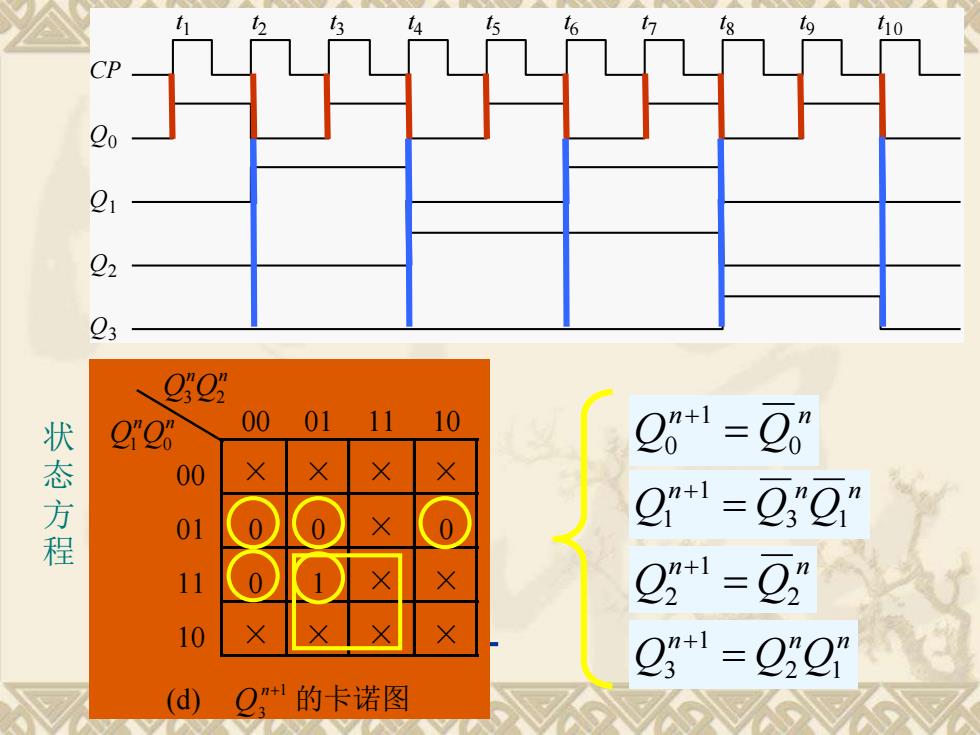
10 02 23 QO: 2"26 00 01 11 10 状态方程 Q8+1=0 00 01 0 g"1=Q"g” 11 O3=0" 10 O-orom (d) 2的卡诺图
(a) 1 0n + Q 的卡诺图 00 01 11 10 00 1 1 × 1 01 0 0 × 0 11 0 0 × × 10 1 1 × × n n Q3 Q2 n n Q1 Q0 CPQ0 Q1 Q2 Q3 t1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 1 0 状态方程 n n Q Q0 1 0 = + (b) 1 1n + Q 的卡诺图 00 01 11 10 00 × × × × 01 1 1 × 0 11 0 0 × × 10 × × × × n n Q3 Q2 n n Q1 Q0 n n n Q Q3 Q1 1 1 = + 00 01 11 10 00 × × × × 01 × × × × 11 1 0 × × 10 × × × × n n Q3 Q2 n n Q1 Q0 (c) 1 2n + Q 的卡诺图 n n Q Q2 1 2 = + 00 01 11 10 00 × × × × 01 0 0 × 0 11 0 1 × × 10 × × × × n n Q3 Q2 n n Q1 Q0 (d) 1 3n + Q 的卡诺图 n n n Q Q2 Q1 1 3 = +

比较,得驱动方程: g"+1="” D。=②” ox=0 D =0"0" Q*1=Q0” D2=O” Q”+1=D D,=Q"Q" 电路图 & FFo FF FF2 FF3 & 0, &1D 0 >C1 将无效状态1010~1111分别代入状态方程进行计算,可以验证 在CP脉冲作用下都能回到有效状态,电路能够自启动
= = = = n n n n n n D Q Q D Q D Q Q D Q 3 2 1 2 2 1 3 1 0 0 = = = = + + + + n n n n n n n n n n Q Q Q Q Q Q Q Q Q Q 2 1 1 3 2 1 2 3 1 1 1 0 1 0 Q D n = +1 比较,得驱动方程: Q0 Q0 Y F F0 FF1 FF2 F F3 Q2 Q2 Q1 Q1 Q3 Q3 1D C1 1D C1 & CP 1D & C1 1D & C1 电路图 将无效状态1010~1111分别代入状态方程进行计算,可以验证 在CP脉冲作用下都能回到有效状态,电路能够自启动