
Chapter4数据链路层 ■4.1数据链路层的基本概念与功能 ■4.2差错检测与校正 ■4.3基本数据链路协议 ■4.4滑动窗口(S1 ide Windows)协议 ■4.5面向位的协议HDLC ■4.6面向字节的数据链路层协议-PPP 16
16 Chapter 4 数据链路层 ◼ 4.1数据链路层的基本概念与功能 ◼ 4.2差错检测与校正 ◼ 4.3基本数据链路协议 ◼ 4.4滑动窗口(Slide Windows)协议 ◼ 4.5面向位的协议HDLC ◼ 4.6面向字节的数据链路层协议-PPP

4.2差错检测与校正 信号在任何信道上传输都存在着传输差错,这 些差错由多种物理现象引起,解决差错问题的 方法有两种: 一 种是在要发送的数据中加入一定的冗余位 使接收方能知道数据是否出错,但不知道是哪 里出错,这种编码方法叫差错检测码,或简称 检错码 。 另一种是在要发送的数据中加入足够多的冗余 位,使接收方能纠正出错的位,这种编码方法 叫差错校正码,或简称纠错码。 17
17 4.2差错检测与校正 ◼ 信号在任何信道上传输都存在着传输差错,这 些差错由多种物理现象引起,解决差错问题的 方法有两种: ◼ 一种是在要发送的数据中加入一定的冗余位, 使接收方能知道数据是否出错,但不知道是哪 里出错,这种编码方法叫差错检测码,或简称 检错码。 ◼ 另一种是在要发送的数据中加入足够多的冗余 位,使接收方能纠正出错的位,这种编码方法 叫差错校正码,或简称纠错码

4.2.1纠错码 定义:一帧由m个数据位(即报文)和r个冗余位(即 校验位)组成,设总长度为n(n=m+r),此长度为n的 单元常称为n位码字。 ■海明距离:两个码字对应位上不相同位的数目称为 例如,10001001与10110001它们的海明距离为3。 ■对于n位码字的集合,只有2m个码字是有效的。 码字集合的海明距离:码字集合中任意两个有效码字 间的最小海明距离,便是该集合的海明距离。 18
18 4.2.1纠错码 ◼ 定义:一帧由m个数据位(即报文)和r个冗余位(即 校验位)组成,设总长度为n(n=m+r),此长度为n的 单元常称为n位码字。 ◼ 海明距离:两个码字对应位上不相同位的数目称为 例如,10001001 与10110001它们的海明距离为3。 ◼ 对于n位码字的集合,只有2 m个码字是有效的。 ◼ 码字集合的海明距离:码字集合中任意两个有效码字 间的最小海明距离,便是该集合的海明距离

一种编码的检错和纠错能力取决于编码后码 字的海明距离的大小。 为了检测出d个比特的错,需要使用距离为 d+1的编码。 例如:数据后加奇偶校验位,编码后的海明距离为2,能检 测1比特错。 ■为了纠正d个比特的错,必须用距离为2d+1 的编码。 例如有4个有效码字:它们的海明距离为5,能纠正2比特错。 0000000000, 0011000000 0000000000 0000011111, 0111000000 1111100000 1111100000, 1111111111, 19
19 ◼ 一种编码的检错和纠错能力取决于编码后码 字的海明距离的大小。 ◼ 为了检测出d个比特的错,需要使用距离为 d+1的编码。 例如:数据后加奇偶校验位,编码后的海明距离为2,能检 测1比特错。 ◼ 为了纠正d个比特的错,必须用距离为2d+1 的编码。 例如有4个有效码字:它们的海明距离为5,能纠正2比特错。 0000000000, 0011000000 0000000000 0000011111, 0111000000 1111100000 1111100000, 1111111111
纠正单比特错的校验位下界 命题:设计一种编码,它有m个信息位和个校验位,当r满 足什么条件时,能纠正所有单比特错? 码字长度n=m+r,总共有2n个种组合,其中有效码字数为2m 每一个有效码字X, 对其某一位取反 有n个与其距离为1的无效码字 例如X=10101010 X1=00101010,X2=11101010 X3=10001010, X4=10111010 X8 2 X5=10100010, X6=10101110 X70 X7=10101000,X8=10101011 2X4 (n+1)2m<=2n,n=m+r代入 X6 得到:2r>=n+1 X5 要纠正单比特错,需采 纠正单比特误码的校验位下界 用距离至少为3的编码 20
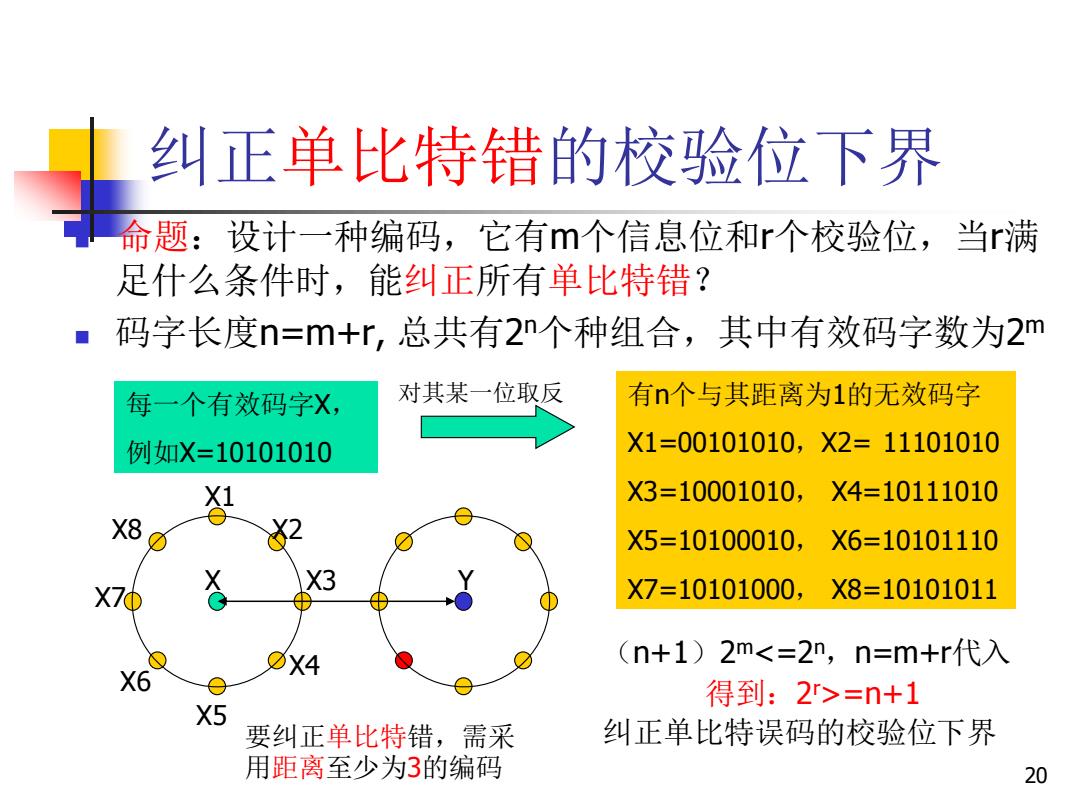
20 纠正单比特错的校验位下界 ◼ 命题:设计一种编码,它有m个信息位和r个校验位,当r满 足什么条件时,能纠正所有单比特错? ◼ 码字长度n=m+r, 总共有2 n个种组合,其中有效码字数为2 m 每一个有效码字X, 例如X=10101010 有n个与其距离为1的无效码字 X1=00101010,X2= 11101010 X3=10001010, X4=10111010 X5=10100010, X6=10101110 X7=10101000, X8=10101011 对其某一位取反 (n+1)2 m<=2n ,n=m+r代入 得到:2 r>=n+1 要纠正单比特错,需采 纠正单比特误码的校验位下界 用距离至少为3的编码 X Y X1 X2 X3 X4 X5 X6 X7 X8