
第十章 重积分
重积分 第十章 重 积 分

第一讲 二重积分的概念
重积分 第一讲 二重积分的概念

重积分 1.二重积分的概念 一、引例 之=fXy) 1.曲顶柱体的体积 给定曲顶柱体: 底:Xoy面上的闭区域D 顶:连续曲面z=fxy)≥0 侧面:以D的边界为准线,母线平行于 z轴的柱面,求其体积. 解法:类似定积分解决问题的思想: “大化小,常代变,近似和,求极限
重积分 1.二重积分的概念 解法: 类似定积分解决问题的思想: 一、引例 1.曲顶柱体的体积 给定曲顶柱体: ᵉ = ᵈ(ᵉ ,ᵉ ) ≥ ᵼ 底: xoy 面上的闭区域 D 顶: 连续曲面 求其体积. “大化小, 常代变, 近似和, 求 极限” ᵆ = ᵅ(ᵆ ,ᵆ )

重积分 1)“大化小” 用任意曲线网分D为n个区域 z=f(xy) △0A02,.,△0 以它们为底把曲顶柱体分为n个 fn) 小曲顶柱体 2)“常代变” Nk 在每个A0专中任取一点传,刀, 则 △Vk≈f5,n)△ok(k=12,.n) 3)“近似和” v=∑4ve-∑f5,0aox k=1
重积分 ᵆ = ᵅ(ᵆ ,ᵆ ) 1)“大化小” ᵱ ᵴ ᵼ ,ᵱ ᵴ ᵽ , ⋯ , ᵱ ᵴ ᵈ 以它们为底把曲顶柱体分为 n 个 2)“常代变” 在每个ᵱ ᵴ ᵈ ( ᵴ ᵈ , ᵳ ᵈ ), 3)“近似和” ᵈ( ᵴ ᵈ , ᵳ ᵈ ) ᵱ ᵇ ᵈ ≈ ᵈ( ᵴ ᵈ , ᵳ ᵈ )ᵱ ᵴ ᵈ (ᵈ = ᵼ ,ᵽ , ⋯ ,ᵈ ) 中任取一点 则 小曲顶柱体 ᵱ ᵴ ᵈ ( ᵴ ᵈ , ᵳ ᵈ )
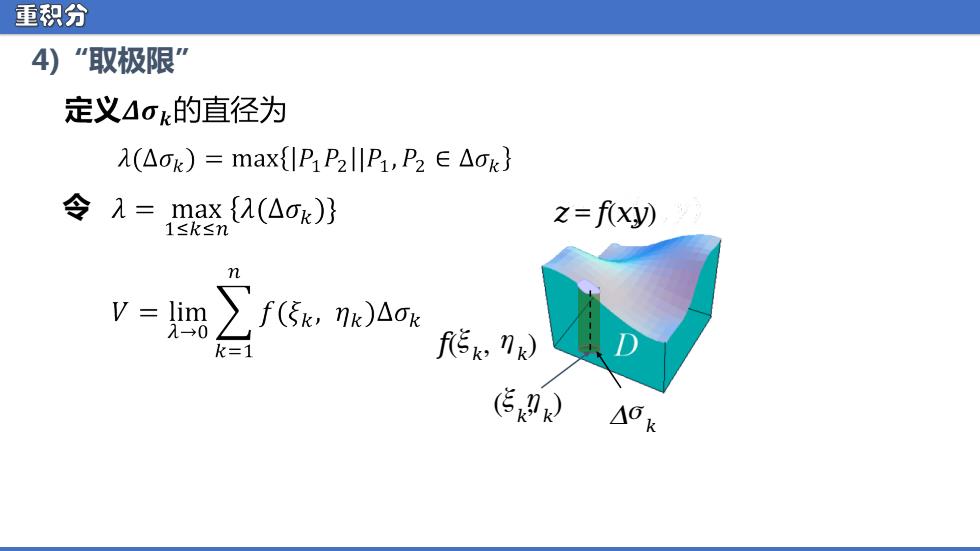
重积分 4)“取极限” 定义Aok的直径为 λ(△ok)=max{P1P2llP1,P2∈△ok} 令λ=max{(△ok)} z=f(xy) 1≤k≤m v(n) 传 )△0k
重积分 4)“取极限” 令 ᵆ = ᵅ(ᵆ ,ᵆ ) ᵅ( ᵰ ᵅ , ᵰ ᵅ ) ᵮ ᵰ ᵅ ( ᵰ ᵅ , ᵰ ᵅ )