
例 单相半波可控整流电路,电阻负载,由220V交流电源直接 供电。负载要求的最高平均电压为60V,相应有效值电流为15.7A,试 计算最大输出时的控制角α,并选择晶闸管元件。 解:(1)先求出最大输出时的控制角α,根据式3-1可得: 2×60 cos a= 2Ud-1= -1=0.212 0.45U2 0.45×220 0=77.8 (2)求晶闸管两端承受的正、反向峰值电压Um: UTM =2U2 =311 机械电气工程学院电气教研室 电力电子技术 3-11
3-11

通子 (3)选择晶闸管: 晶闸管通态平均电流,可按下式计算与选择: 1m=05-2多7=05-21715-204 、15.7 取IT(A)=20A 晶闸管电压定额可按下式计算与选择: Um=(2~3)UM=622~933V 取 Um=1000V 可选用KP20-10型晶闸管。 机械电气工程学院电气教研室 电力电子技术 3-12
3-12
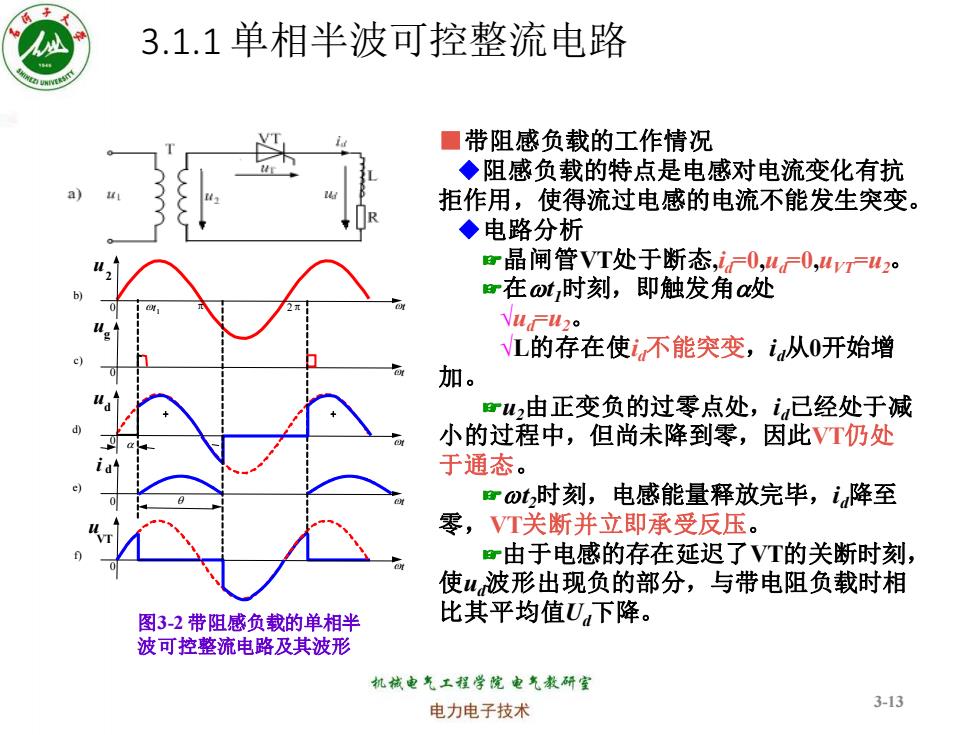
3.1.1单相半波可控整流电路 ■带阻感负载的工作情况 ◆阻感负载的特点是电感对电流变化有抗 拒作用,使得流过电感的电流不能发生突变。 ◆电路分析 晶闸管VT处于断态,i0,40,4v广42o r在ot,时刻,即触发角a处 NuFu2o VL的存在使i不能突变,i从0开始增 加。 ru2由正变负的过零点处,i已经处于减 小的过程中,但尚未降到零,因此VT仍处 于通态。 rωt时刻,电感能量释放完毕,i降至 零,VT关断并立即承受反压。 r由于电感的存在延迟了VT的关断时刻, 使u,波形出现负的部分,与带电阻负载时相 图3-2带阻感负载的单相半 比其平均值U下降。 波可控整流电路及其波形 机械电气工程学院电气教研室 电力电子技术 3-13
3.1.1 单相半波可控整流电路 3-13 u wt wt wt wt w 2 0 wt 1 p 2 p t u g 0 ud 0 i d 0 u VT 0 q a b) c) d) e) f) + + 图3-2 带阻感负载的单相半 波可控整流电路及其波形 ■带阻感负载的工作情况 ◆阻感负载的特点是电感对电流变化有抗 拒作用,使得流过电感的电流不能发生突变。 ◆电路分析 ☞晶闸管VT处于断态,id=0,ud=0,uVT=u2。 ☞在wt1时刻,即触发角a处 √ud=u2。 √L的存在使id不能突变,id从0开始增 加。 ☞u2由正变负的过零点处,id已经处于减 小的过程中,但尚未降到零,因此VT仍处 于通态。 ☞wt2时刻,电感能量释放完毕,id降至 零,VT关断并立即承受反压。 ☞由于电感的存在延迟了VT的关断时刻, 使ud波形出现负的部分,与带电阻负载时相 比其平均值Ud下降
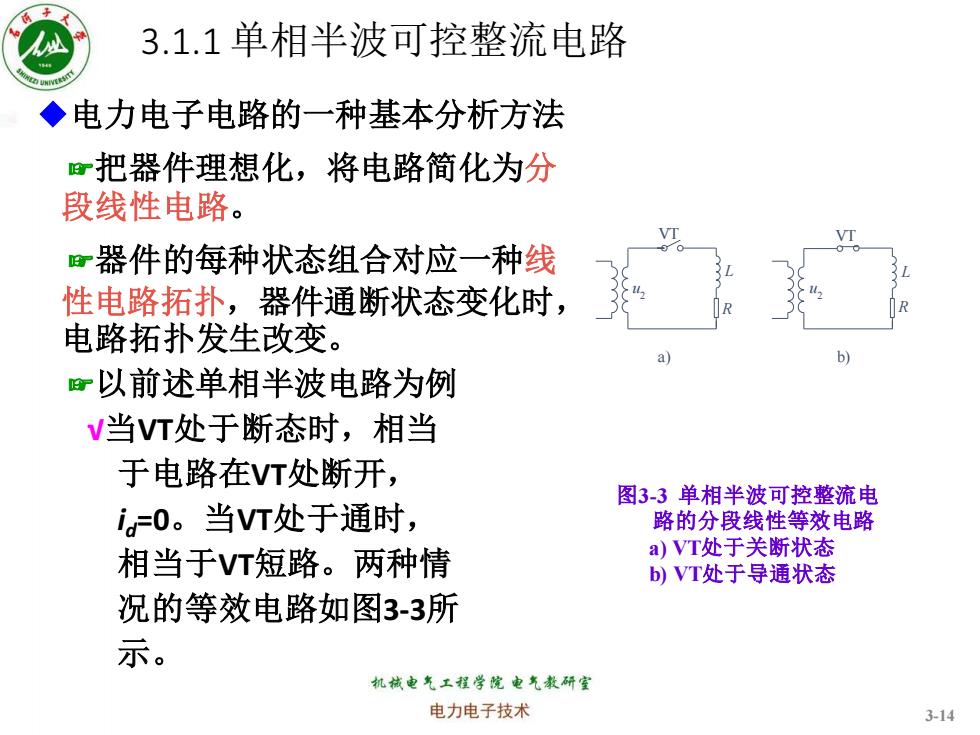
3.1.1单相半波可控整流电路 ◆电力电子电路的一种基本分析方法 r把器件理想化,将电路简化为分 段线性电路。 旷器件的每种状态组合对应一种线 性电路拓扑,器件通断状态变化时, 电路拓扑发生改变。 6 以前述单相半波电路为例 V当VT处于断态时,相当 于电路在VT处断开, 图3-3单相半波可控整流电 i=0。当VT处于通时, 路的分段线性等效电路 相当于VT短路。两种情 a)VT处于关断状态 b)VT处于导通状态 况的等效电路如图33所 示。 机械电气工程学院电气教研室 电力电子技术 3-14
3.1.1 单相半波可控整流电路 ◆电力电子电路的一种基本分析方法 ☞把器件理想化,将电路简化为分 段线性电路。 ☞器件的每种状态组合对应一种线 性电路拓扑,器件通断状态变化时, 电路拓扑发生改变。 ☞以前述单相半波电路为例 √当VT处于断态时,相当 于电路在VT处断开, id=0。当VT处于通时, 相当于VT短路。两种情 况的等效电路如图3-3所 示。 a) b) VT R L VT R L u2 u2 3-14 图3-3 单相半波可控整流电 路的分段线性等效电路 a) VT处于关断状态 b) VT处于导通状态
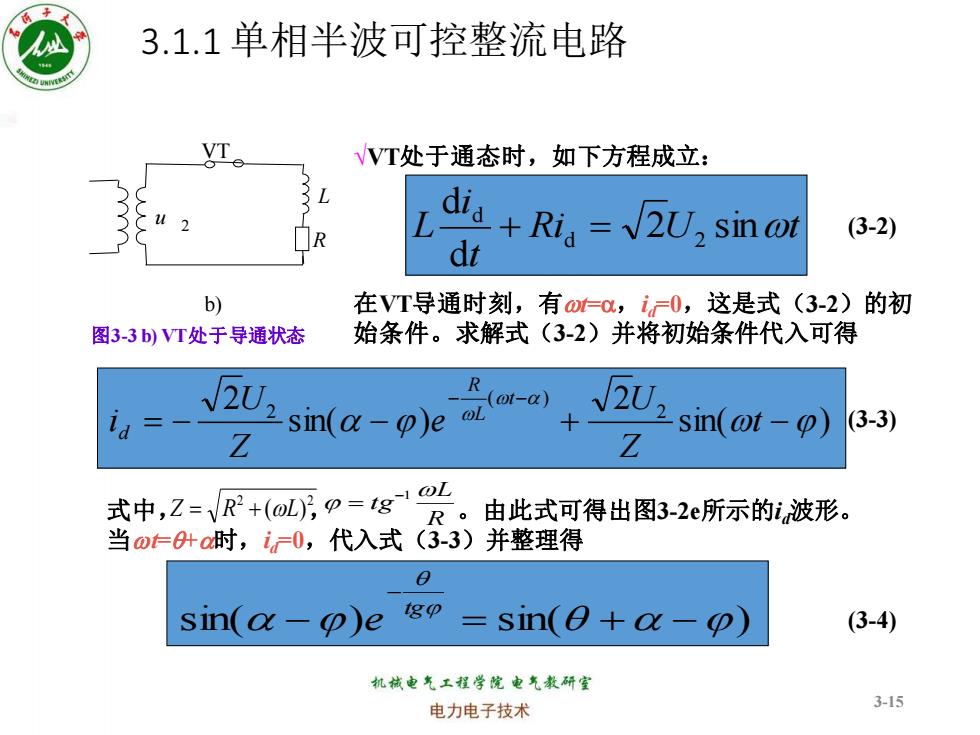
3.1.1单相半波可控整流电路 VVT处于通态时,如下方程成立: di (3-2) dt +Rig=U2 sin @t b) 在VT导通时刻,有o-c,i0,这是式(3-2) 的初 图3-3b)VT处于导通状态 始条件。求解式(3-2)并将初始条件代入可得 √2U2 R Z sin(a-)e oi (ot-a) sin(o-)-3) Z 式中,Z=VR2+(olp=g1 R。 由此式可得出图3-2e所示的i,波形。 当o什o时,0,代入式(3-3)并整理得 a sin(a-p)e =sin(0+a -p) (3-4) 机械电气工程学院电气教研室 电力电子技术 3-15
3.1.1 单相半波可控整流电路 3-15 VT b) R L u 2 √VT处于通态时,如下方程成立: 在VT导通时刻,有wt=a,id=0,这是式(3-2)的初 始条件。求解式(3-2)并将初始条件代入可得 Ri U t t i L 2 sinw d d d 2 d + = sin( ) 2 sin( ) 2 2 ( ) 2 a w w a w = − − + − − − t Z U e Z U i t L R d 式中, , 。由此式可得出图3-2e所示的id波形。 当wt=q+a时,id=0,代入式(3-3)并整理得 2 2 Z = R + (wL) R L tg w −1 = sin(a ) sin(q a ) q − = + − − tg e 图3-3 b) VT处于导通状态 (3-2) (3-3) (3-4)