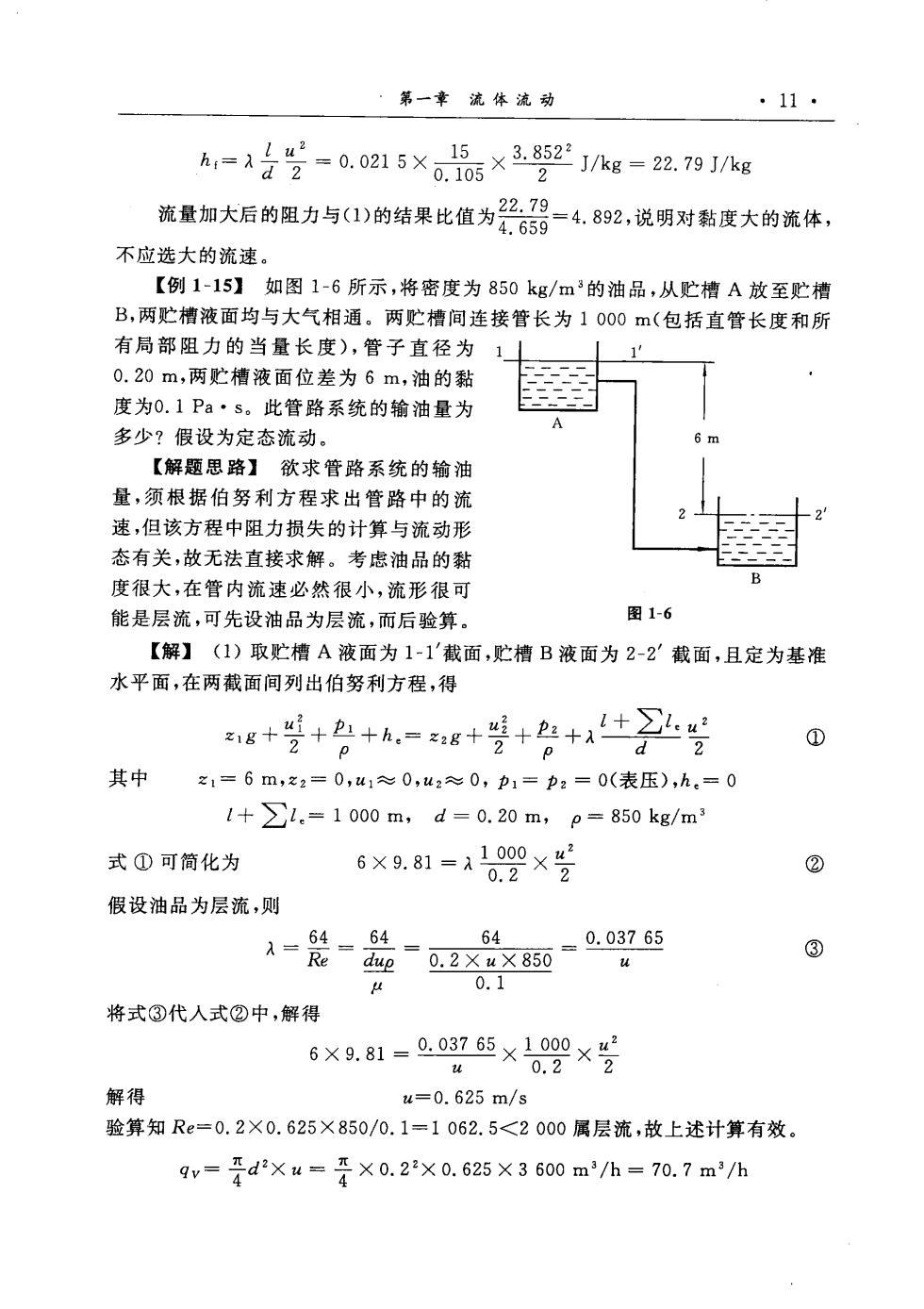
第一章流体流动 ·11· =-0.0215s×3852kg=2791e 放量加大后的阻为与1)的结果比值为器。器=4.892,说明对黏度大的流体。 不应选大的流速。 【例1-15】如图1-6所示,将密度为850kg/m3的油品,从贮槽A放至贮槽 B,两贮槽液面均与大气相通。两贮槽间连接管长为1000m(包括直管长度和所 有局部阻力的当量长度),管子直径为 1 0.20m,两贮槽液面位差为6m,油的黏 度为0.1Pa·s。此管路系统的输油量为 多少?假设为定态流动。 【解题思路】欲求管路系统的输油 量,须根据伯努利方程求出管路中的流 速,但该方程中阻力损失的计算与流动形 态有关,故无法直接求解。考虑油品的黏 度很大,在管内流速必然很小,流形很可 能是层流,可先设油品为层流,而后验算。 图1-6 【解】(1)取贮槽A液面为1-1'截面,贮槽B液面为2-2截面,且定为基准 水平面,在两截面间列出伯努利方程,得 g+号+色+.=g+盟+g++☒写 ⊙ 其中21=6m,之2=0,41≈0,u2≈0,p1=p2=0(表压),h.=0 1+l.=1000m,d=0.20m,p=850kg/m 式①可简化为 6×9.81=2×号 ② 假设油品为层流,则 A- 64 ③ 0.1 将式③代人式②中,解 6x9.81-008765×62×号 赵 解得 u=0.625m/s 验算知Re=0.2×0.625×850/0.1=1062.5<2000属层流,故上述计算有效。 9v=年d2Xu=平×0.22×0.625×3600m'/h=70.7m/h

·12· 化工原理学习辅导与习随解答 【例1-16】散口容器的侧壁装有 内径为25mm的短管,用以排水。水 以4.5m2/h的流量连续加入容器内, 以维持液面恒定,如图1-7所示。试求 容器中的水位高度。 【解题思路】本题属于定态流动, 根据水的体积流量可求得短管中的流 图1-7 速,再由伯努利方程即可求得容器的水 位高度。 【解】短管中的流速 4.5 3600 m/s=2.55m/s 工×0.0252 在容器的恒定液面1-1'及侧壁短管出口外侧2-2截面间列伯努利方程(以短 管中心线为基准面),得 g++色+h.=g++色+∑h, 0 其中 p1=0(表压),p2=0(表压),u1≈0,h.=0,z2=0,42=0 故 z1g=∑h 因放水管很短,可以忽略直管阻力,即 ∑h≈(G+5)=1+0.5)× 故 z21g=1.5×5-1.5×2.55 2 解得 21=0.497m 【例1-17】如图1-8所示,将减压条件下的水蒸气送入冷凝器中,与由上方 进人的怜水相遇而冷凝,因水处于减压状态,必须靠重力作用才能自动通过气压管 排出。气压管插在水封槽中,在排出冷凝水的同时,又可防止外界空气漏入设备 内。已知真空表上的读数为7.8×10Pa,图中p,为冷凝管内的绝对压力。试求 气压管中水上升的高度h。 【解题思路】本题可根据静力学方程求得气压管中的液封高度。 【解】以水封槽的水面为参考面。于其上取点2及点2。点2取在水封槽水 面上,点2取在气压管内与水封槽水面等高处,则:=2 又 p2=p。,p2=p1十0*gh 故 p.=p1+P*gh=(p,-7.8×10)+1000×9.81×h
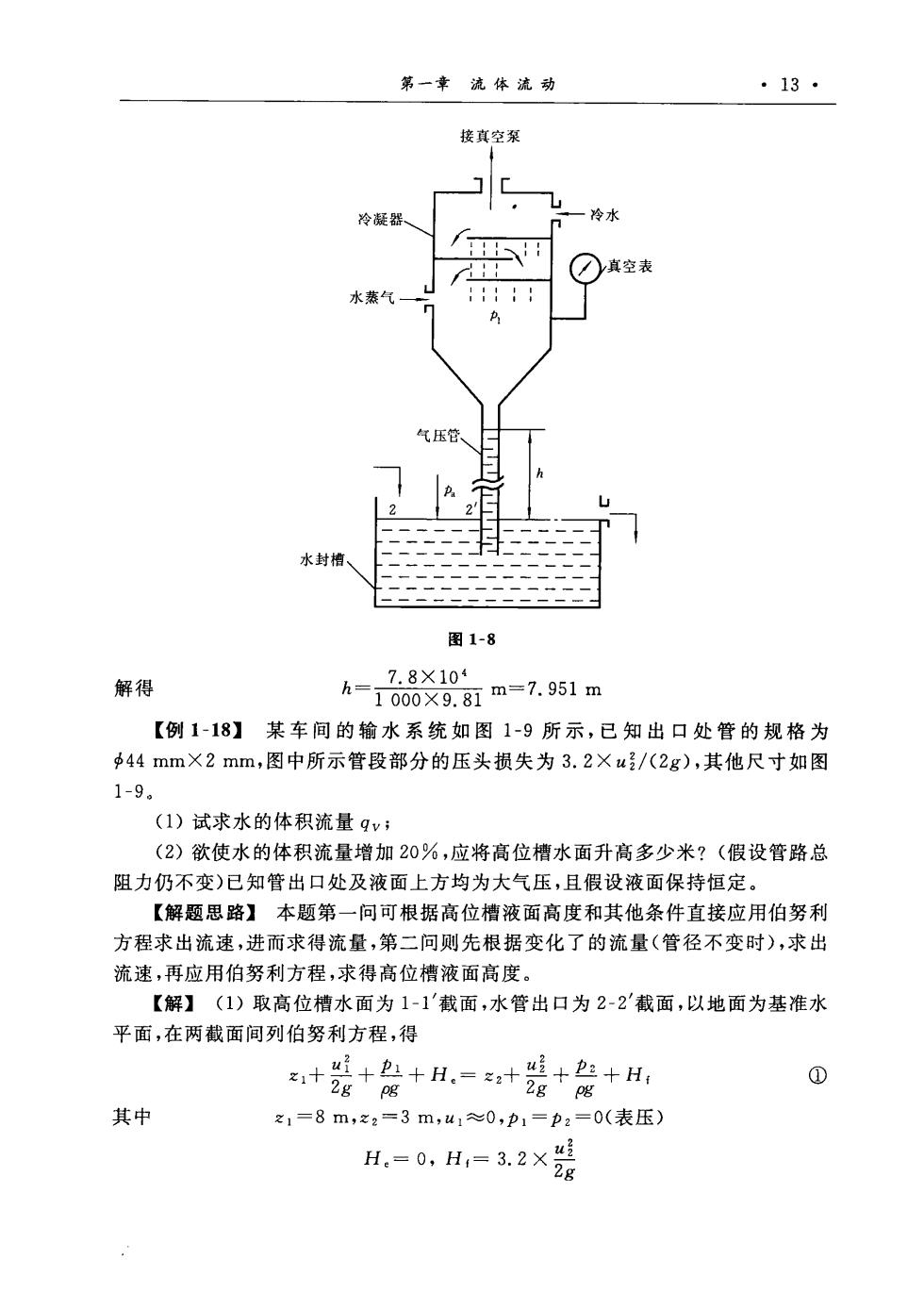
第一章流体流动 ·13· 接真空泵 空表 水蒸气 气压管 水封植 图1-8 解得 A18X1a=7,951m 【例1-18】某车间的输水系统如图1-9所示,已知出口处管的规格为 44mm×2mm,图中所示管段部分的压头损失为3.2×u/(2g),其他尺寸如图 1-9。 (1)试求水的体积流量qv; (2)欲使水的体积流量增加20%,应将高位槽水面升高多少米?(假设管路总 阻力仍不变)已知管出口处及液面上方均为大气压,且假设液面保持恒定。 【解题思路】本题第一问可根据高位槽液面高度和其他条件直接应用伯努利 方程求出流速,进而求得流量,第二问则先根据变化了的流量(管径不变时),求出 流速,再应用伯努利方程,求得高位槽液面高度。 【解】(1)取高位槽水面为1-1'截面,水管出口为2-2截面,以地面为基准水 平面,在两截面间列伯努利方程,得 +装+是+,=+是+是+H, 0 其中 21=8m,2:=3m,41≈0,p1=p:=0(表压) H.=0.H=32x装
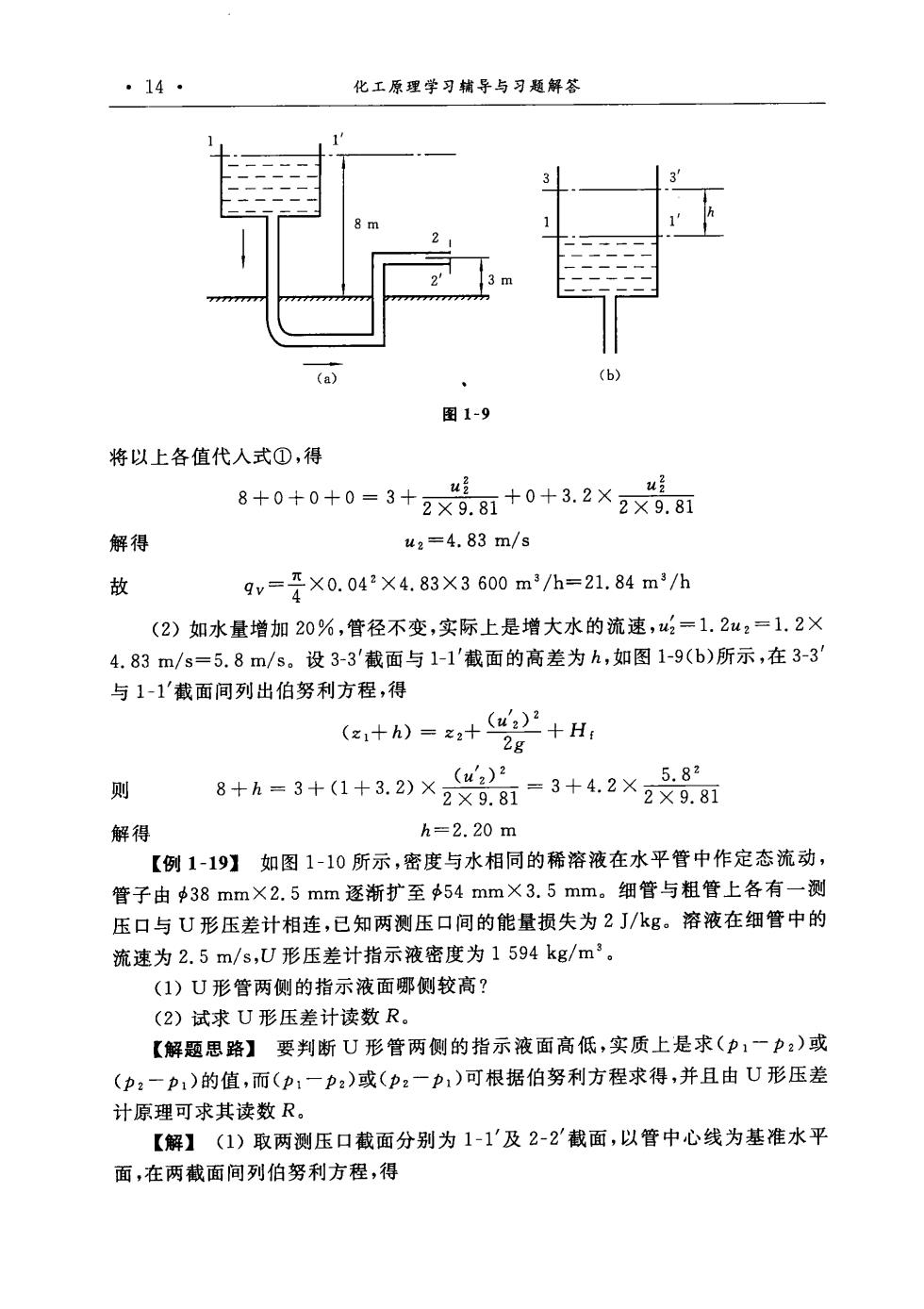
·14- 化工原理学习辅导与习题解答 图1-9 将以上各值代人式①,得 8+0+0+0=3+2x号.+0+3.2×2x. 解得 u2=4.83m/s 故 9v=×0.042×4.83X3600m/h=21.84m3/h (2)如水量增加20%,管径不变,实际上是增大水的流速,=1.2u2=1.2× 4.83m/s=5.8m/s。设3-3截面与1-1'截面的高差为h,如图1-9(b)所示,在3-3 与1-1'截面间列出伯努利方程,得 (+)=4t)2+H 2g 8+A=3++32×-3+42X3装8 解得 h=2.20m 【例1-19】如图1-10所示,密度与水相同的稀溶液在水平管中作定态流动, 管子由38mm×2.5mm逐渐扩至54mm×3.5mm。细管与粗管上各有一测 压口与U形压差计相连,已知两测压口间的能量损失为2J/kg。溶液在细管中的 流速为2.5m/s,U形压差计指示液密度为1594kg/m’。 (1)U形管两侧的指示液面哪侧较高? (2)试求U形压差计读数R。 【解题思路】要判断U形管两侧的指示液面高低,实质上是求(p1一p:)或 (p,一p1)的值,而(p1一p:)或(p:一p1)可根据伯努利方程求得,并且由U形压差 计原理可求其读数R。 【解】(1)取两测压口截面分别为1-1'及2-2截面,以管中心线为基准水平 面,在两截面间列伯努利方程,得
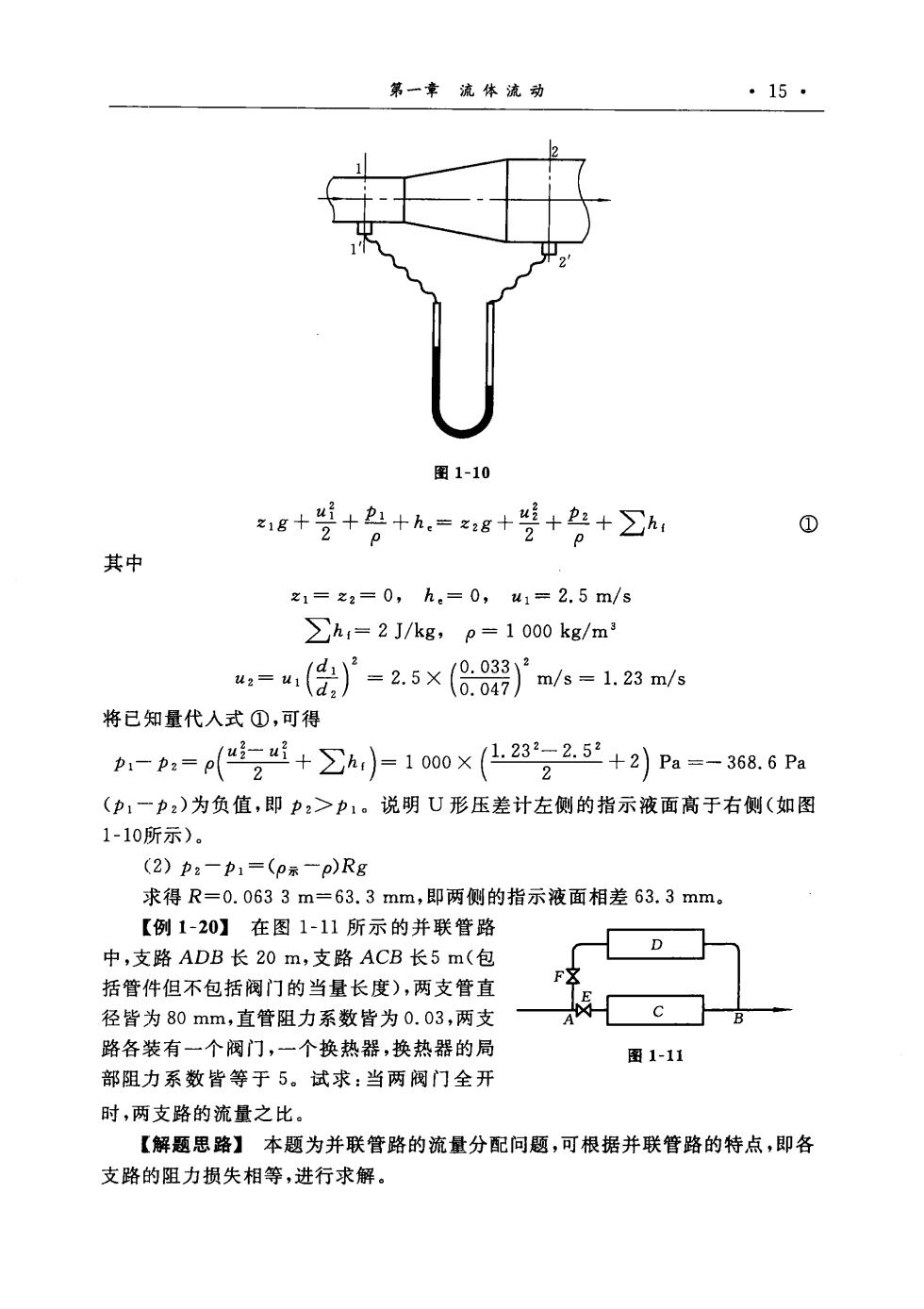
第一章流体流动 ·15. 图1-10 1g++色+h,=g+盟+色+∑, 其中 z1=z2=0,h,=0,u1=2.5m/s ∑h=2J/kg,p=1000kg/m :=(经}-2.5×(8}ms=1.23a/6 将已知量代入式①,可得 p-p:=p34+∑)=100×(2322.5+2)P=-36.6Pa 2 (p1一p2)为负值,即p2>p1。说明U形压差计左侧的指示液面高于右侧(如图 1-10所示)。 (2)p2一p1=(p示-p)Rg 求得R=0.0633m=63.3mm,即两侧的指示液面相差63.3mm。 【例1-20】在图1-11所示的并联管路 中,支路ADB长20m,支路ACB长5m(包 括管件但不包括阀门的当量长度),两支管直 径皆为80mm,直管阻力系数皆为0.03,两支 路各装有一个阀门,一个换热器,换热器的局 图1-11 部阻力系数皆等于5。试求:当两阀门全开 时,两支路的流量之比。 【解题思路】本题为并联管路的流量分配问题,可根据并联管路的特点,即各 支路的阻力损失相等,进行求解