
§7.1无损介质中的均匀平面波 写成分量: (+z方向传播)/应=7 , /H=-n (-z方向传播)E/H,=-n E./H.=n (1)对复数值和瞬时值均成立 +2,- (2)仅对每个行波成立,对合 行+,i 成场不一定成立
§ 7.1 无损介质中的均匀平面波 写成分量 z EH 写成分量: ( 方向传播) E E x y y x z EH E H ( 方向传播) E E, x y z EH ( 方向传播) 1 E y x H (1)对复数值和瞬时值均成立 z z ˆ ˆ 2 ()对复数值和瞬时值均成立 ( )仅对每个行波成立,对合 H H z z , 成场不一定成立 H H

§7.1无损介质中的均匀平面波 ③每个行波的电场能量密度等于磁场能量密度(瞬时, 平均),能量的传播方向即为波的传播方向 w=(e,0=e7i(e,0x±到 oio时- 5*=Ex=×(±金×E) =±{(E)(e》=±=切7f:
§ 7.1 无损介质中的均匀平面波 ③每个行波的电场能量密度等于磁场能量密度(瞬时, 1 1 平均),能量的传播方向即为波的传播方向 2 2 (,) (,) ( )ˆ 2 2 w E zt H zt z e 2 2 1 1 2 H zt H zt w (,) (,) (,) (,) 2 2 1 ˆ H zt H zt wm S E H E zE 1 1 2 2 S E H E zE 1 1 2 2 zˆ ˆ ˆˆ E E E zE E z H z

§7.1无损介质中的均匀平面波 例:已知自由空间中B=106c0s(6π×103t-2πz)(父+), 试求:(1)f,,B以及传播方向;(2)E的表达式 (3)S的表达式;( 4)若在yoz平面放置一半径为R的 圆环,P为多少? 解:) 波沿+Z轴方向传播;B=2π(rad/m) 2=2π/B=1(m,f=o/2π=3×10°(m/s) (2疗=1元=10e(G+) 6 46 no-Hy H
§ 7.1 无损介质中的均匀平面波 6 8 B 10 cos(6 10 2 t zx )( ) ˆ yˆ 例:已知自由空间中 ( )( ), 1 ,, 2 y f E 例 知自由空间中 , 试求:() 以及传播方向;( ) 的表达式 S R P (3) 的表达式;(4)若在yoz平面放置一半径为 的 圆环,P为多少? 解:()波沿 轴方向传播; ( 1 2/ Z rad m ) 8 ) 2 / 1( ), / 2 3 10 ( / ) m f ms 6 2 0 10 (2) () ˆ ˆ j Z Ex Ey HB ex y 1 0 0 () ( ) y x y H H 0

§7.1无损介质中的均匀平面波 E,=-H=-V4/8o(B/4,)=-vB=-300e2 Ex=7立,=vB,=300e2: E=300cos(6π×108t-2πz)(父-)(V/m) (3)S=ExH= 300×106 4rx107c0s'(6zx10 =477.4cos2(6π×103t-2πz)2(0 (④P=f(E×面S=0 x
§ 7.1 无损介质中的均匀平面波 2 0 00 0 ( ) 300 j z Eyx x x H B vB e 0 00 0 2 0 ( ) 300 yx x x j z E H vB e x yy 8 E t zx 300cos(6 10 2 ) ( ˆ yˆ) ( / V m) 6 2 8 7 300 10 (3) cos (6 10 2 ) ( ) ( ) ˆˆ ˆˆ 4 10 S EH t z x y x y 2 8 2 477.4cos (6 1 0 2) t z zˆ (W m/ ) (4) ( ) 0 s P E H dS
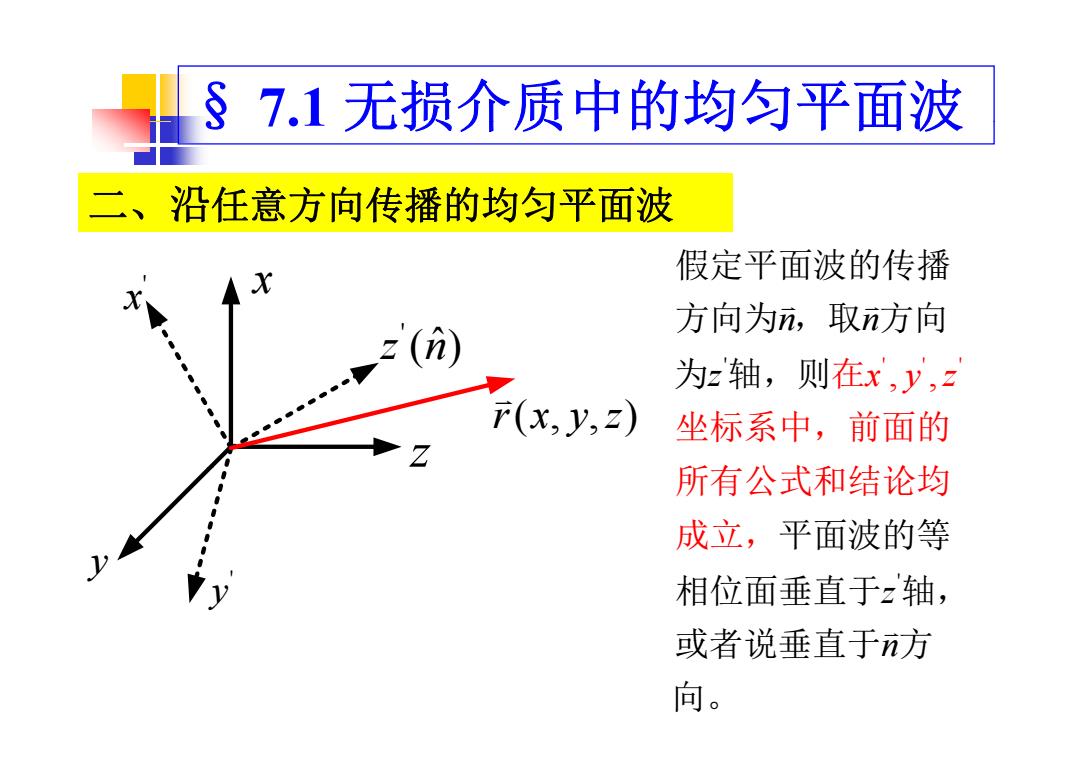
§7.1无损介质中的均匀平面波 二、沿任意方向传播的均匀平面波 假定平面波的传播 方向为n,取n方向 为z轴,则在x,y,z F(x,y,z) 坐标系中,前面的 所有公式和结论均 成立,平面波的等 相位面垂直于z轴, 或者说垂直于n方 向
§ 7.1 无损介质中的均匀平面波 二、沿任意方向传播的均匀平面波 ' x x 假定平面波的传播 ' z n( )ˆ ' ' ' ' n n z xyz 在 方向为 ,取 方向 为 轴,则 z rxyz (, ,) z 在xyz , , 坐标系中,前面的 所有公式和结论均 为 轴,则 所有公式和结论均 成立,平面波的等 y ' y ' z n 相位面垂直于 轴, 或者说垂直于n方 向