
同步电机的空间坐标系统 三8 磁极相对电枢旋转并依次 经过ABC相相轴为正相序 空间轴线的定义 D 相轴ABC 相绕组输入正电流时产生气隙 B C定子 磁势基波幅值空间位置。 ABC系统 2) 直轴d 磁极N极磁场基波幅值位置。 3) 交轴q 沿转子转向且超前直轴90电角 度的位置。 转子 q系 2022-3-12 11
2022-3-12 11 同步电机的空间坐标系统 磁极相对电枢旋转并依次 经过ABC相相轴为正相序 空间轴线的定义 1) 相轴ABC 相绕组输入正电流时产生气隙 磁势基波幅值空间位置。 2) 直轴d 磁极N极磁场基波幅值位置。 3) 交轴q 沿转子转向且超前直轴900电角 度的位置。 N S d q A 定子 ABC系统 转子 dq系统 N S B C A
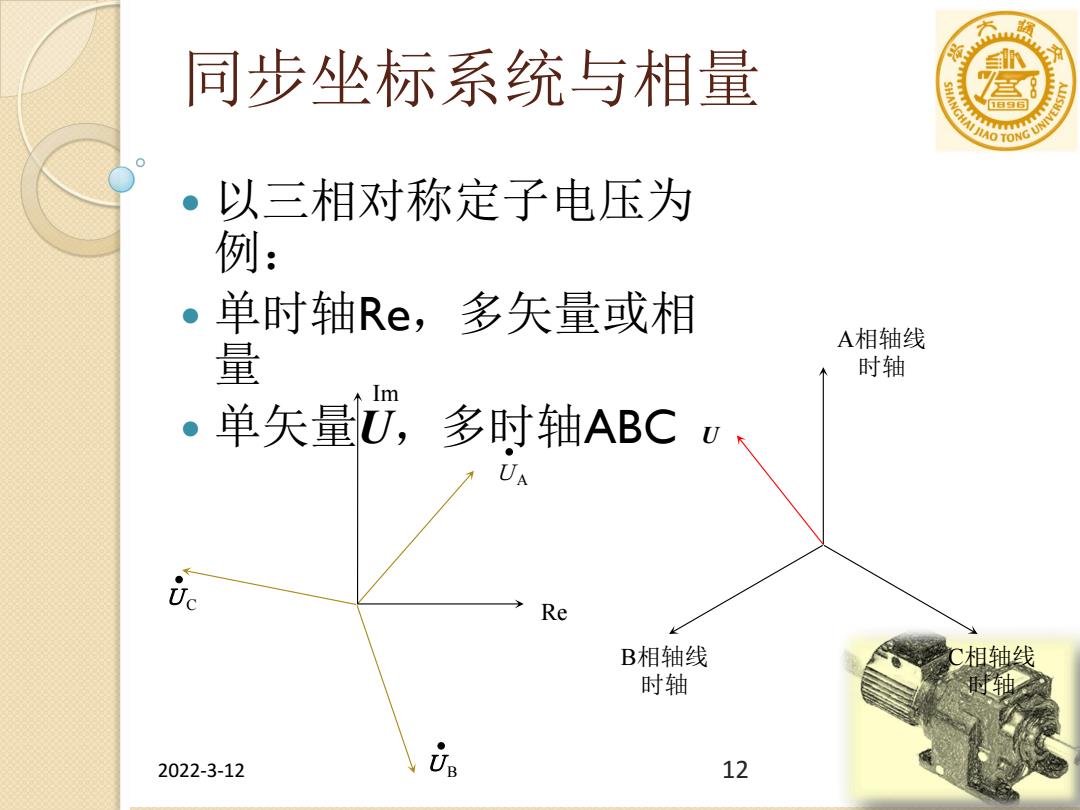
同步坐标系统与相量 宫8 0 以三相对称定子电压为 例: 0 单时轴Re,多矢量或相 A相轴线 量 时轴 m ·单矢量U,多时轴ABC Uc Re B相轴线 C相轴线 时轴 时轴 2022-3-12 12
2022-3-12 12 同步坐标系统与相量 以三相对称定子电压为 例: 单时轴Re,多矢量或相 量 单矢量U,多时轴ABC A相轴线 时轴 B相轴线 时轴 C相轴线 时轴 U Re Im UA UB UC
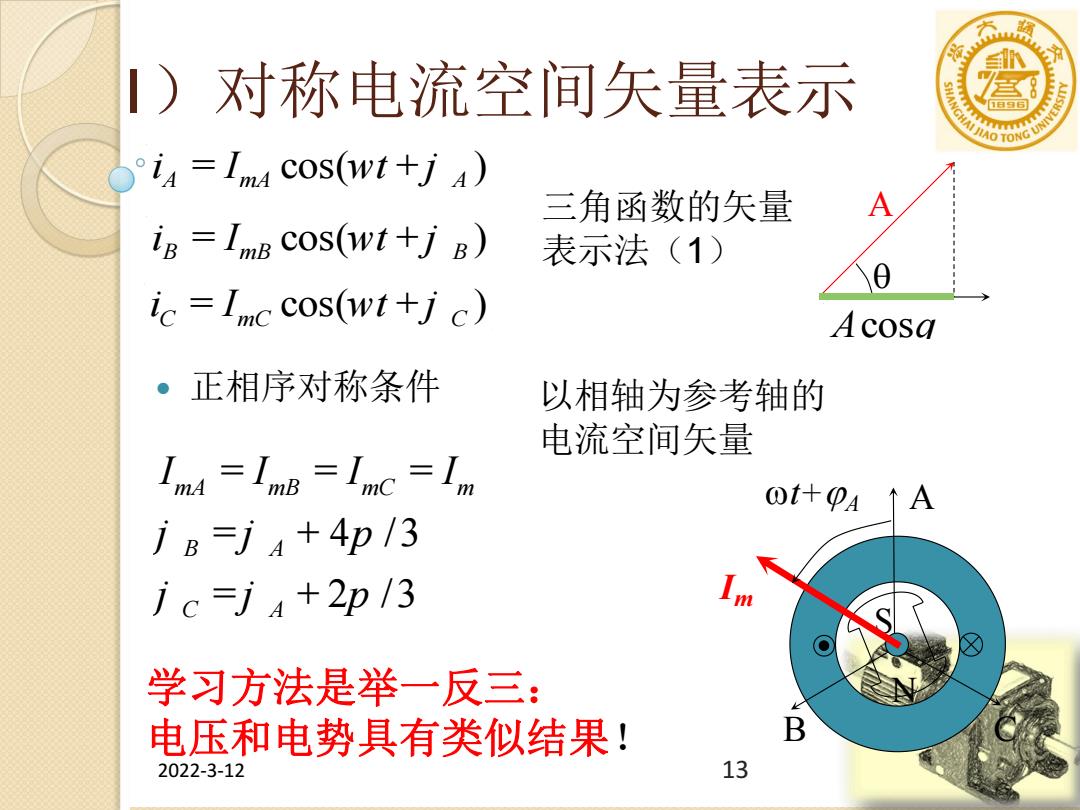
!)对称电流空间矢量表示 8 °iA=Imd cos(wt+jA) 三角函数的矢量 A ig ImB cos(wt+j B) 表示法(1) ic lmc cos(wt+j c) Acosa 。正相序对称条件 以相轴为参考轴的 电流空间矢量 Im4 =Ime Imc Im Ot什pA↑A j&=j+4p/3 jc=j4+2p/3 m 学习方法是举一反三: 电压和电势具有类似结果! B 2022-3-12 13
2022-3-12 13 1)对称电流空间矢量表示 正相序对称条件 iA = ImA cos(wt + j A ) iB = ImB cos(wt + j B ) iC = ImC cos(wt + j C ) Acosq A ImA = ImB = ImC = Im j B = j A + 4p /3 j C = j A + 2p /3 三角函数的矢量 表示法(1) N S B C A Im t+A 以相轴为参考轴的 电流空间矢量 学习方法是举一反三: 电压和电势具有类似结果!

2)双旋转磁场理论 宫8 每相轴线上的磁势最大: 三角函数的矢量 表示法(2) F=F cos(wt+j) FB =Fmg cos(wt+j B) cosq =ie+e Fc=Fc cos(wt+j c) A=A/2 ·对称条件 Acosq Fm4 FmB Fuc=Fm jB=j4+4p/3 A=A/2 jc=j4+2p13 双旋转磁场理论 2022-3-12 14
2022-3-12 14 2)双旋转磁场理论 对称条件 FA = FmA cos(wt + j A ) FB = FmB cos(wt + j B ) Acosq A+ =A/2 A-=A/2 FmA = FmB = FmC = Fm j B = j A + 4p /3 j C = j A + 2p /3 三角函数的矢量 表示法(2) FC = FmC cos(wt + j C ) cosq = 1 2 e jq + 1 2 e - jq 每相轴线上的磁势最大: 双旋转磁场理论
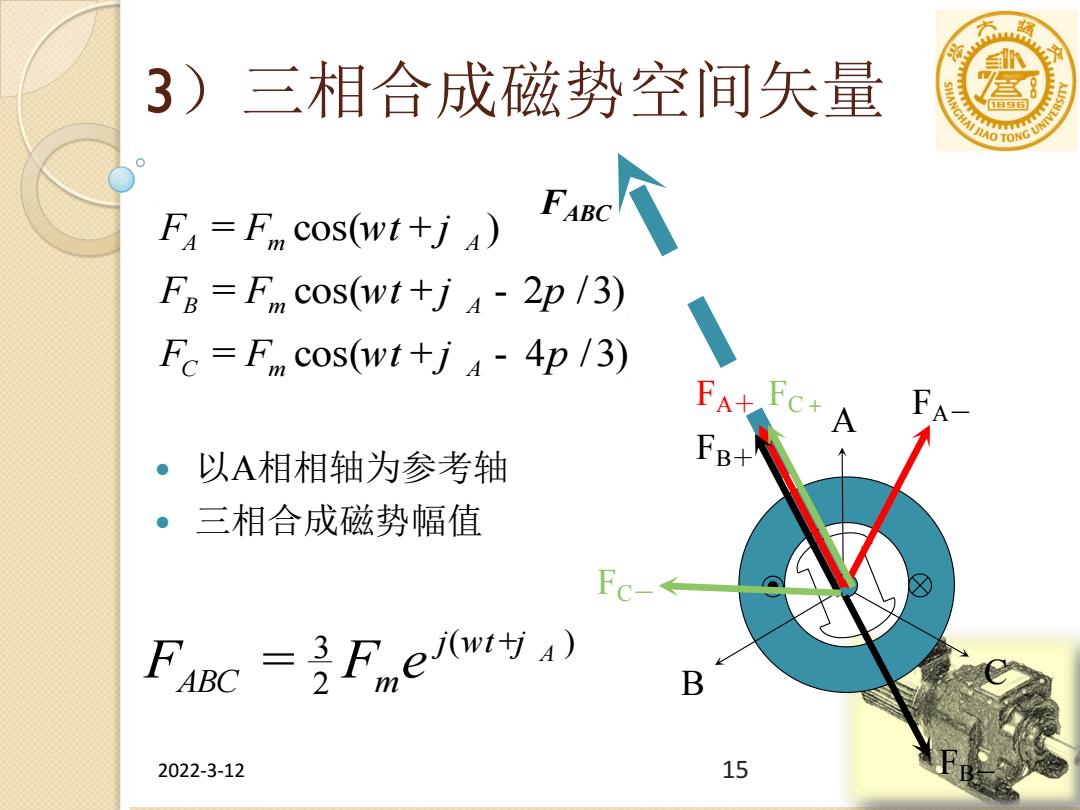
3)三相合成磁势空间矢量 宫8 F=F cos(wt+j) FB F cos(wt+j a-2p /3) Fc=F cos(wt+j-4p /3) F 以A相相轴为参考轴 三相合成磁势幅值 Fc- FANC=3Fe/ B 2022-3-12 15
2022-3-12 15 3)三相合成磁势空间矢量 FA = Fm cos(wt + j A ) FB = Fm cos(wt + j A - 2p /3) FC = Fm cos(wt + j A - 4p /3) FABC = 3 2 Fme j(wt +j A ) 以A相相轴为参考轴 三相合成磁势幅值 B C A FA+ FA- FB+ FC+ FB- FC- FABC