§3.2费马原理(Fermat'sPrinciple) 1.光程定义: L=ns 因此,光在介质中走过的光程,等于以相同的时 间在真空中走过的距离. B nds
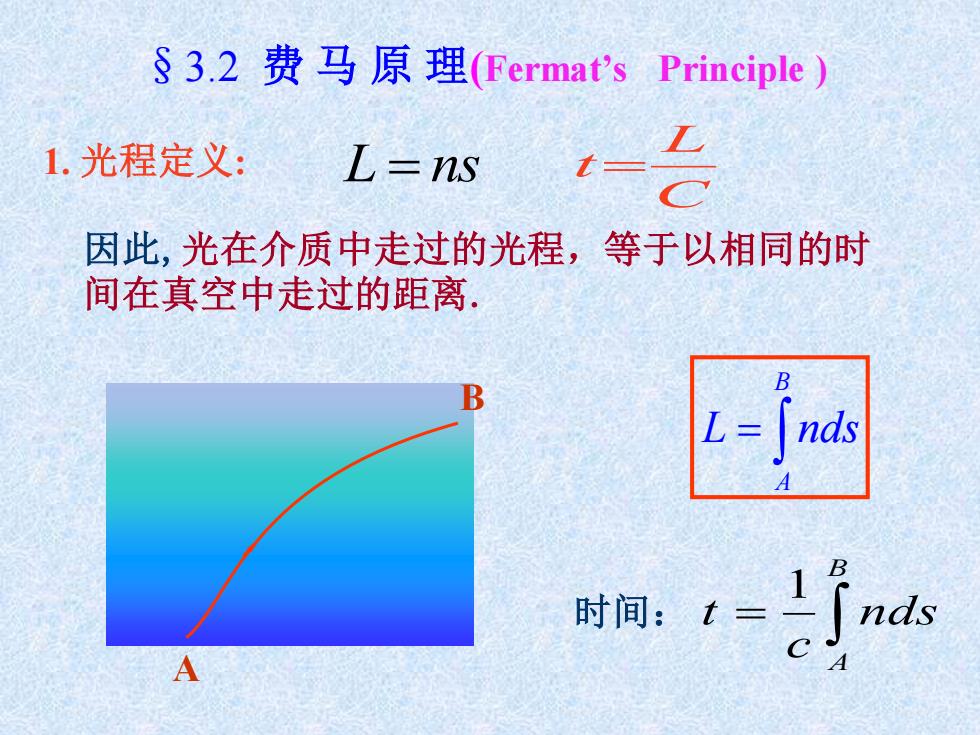
§3.2 费 马 原 理(Fermat’s Principle ) 1. 光程定义: 因此,光在介质中走过的光程,等于以相同的时 间在真空中走过的距离. L = ns C L t= B A = B A L nds 时间: = B A nds c t 1

2.费马原理 光在指定的两点间传播,实际的光程总是一个极值 ∫ndk=极值 数学描述 =jn=0 (1)光程为极小值
2. 费马原理 光在指定的两点间传播,实际的光程总是一个极值 = B A nds 极值 数学描述 = = B A L nds 0 (1) 光程为极小值 B C D A E B
(2)等光程的例子 回转椭球凹面镜 (3)光程为极大值
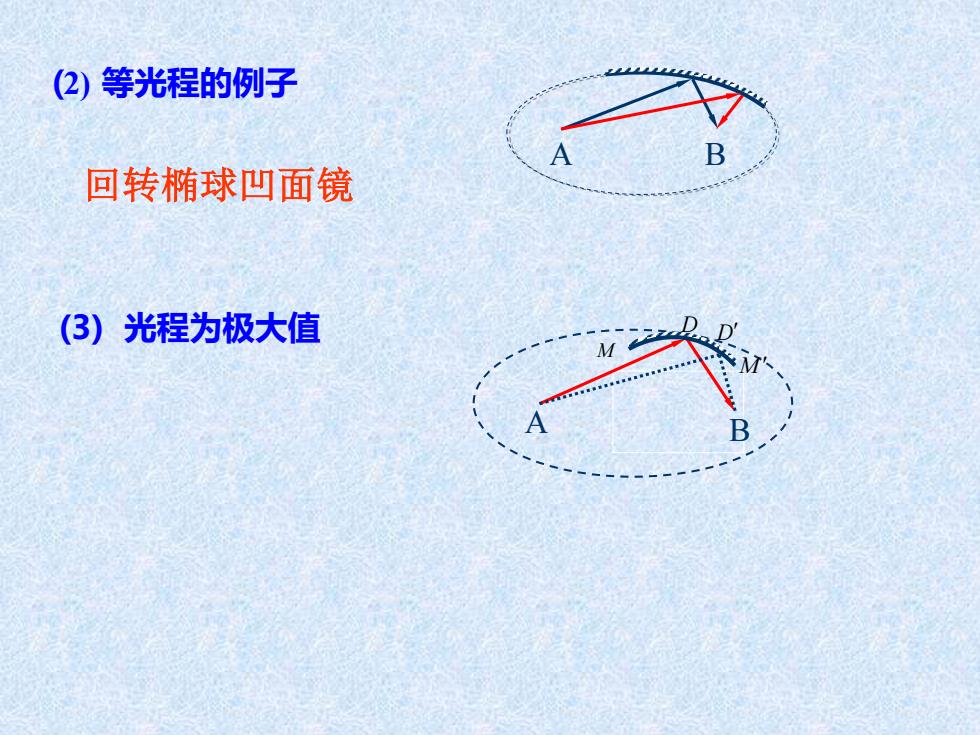
(2) 等光程的例子 A B (3) 光程为极大值 A B M M D D 回转椭球凹面镜
由费马原理证明折射定律: 设A点的坐标为(x,0,z1) B点的坐标为(x2,0,2) P点为入射光线与界面的交点, 其坐标为(x,y,0) n 令AP=L1,PB=L2 B 由A点到B点的光程为: L=nL+nL
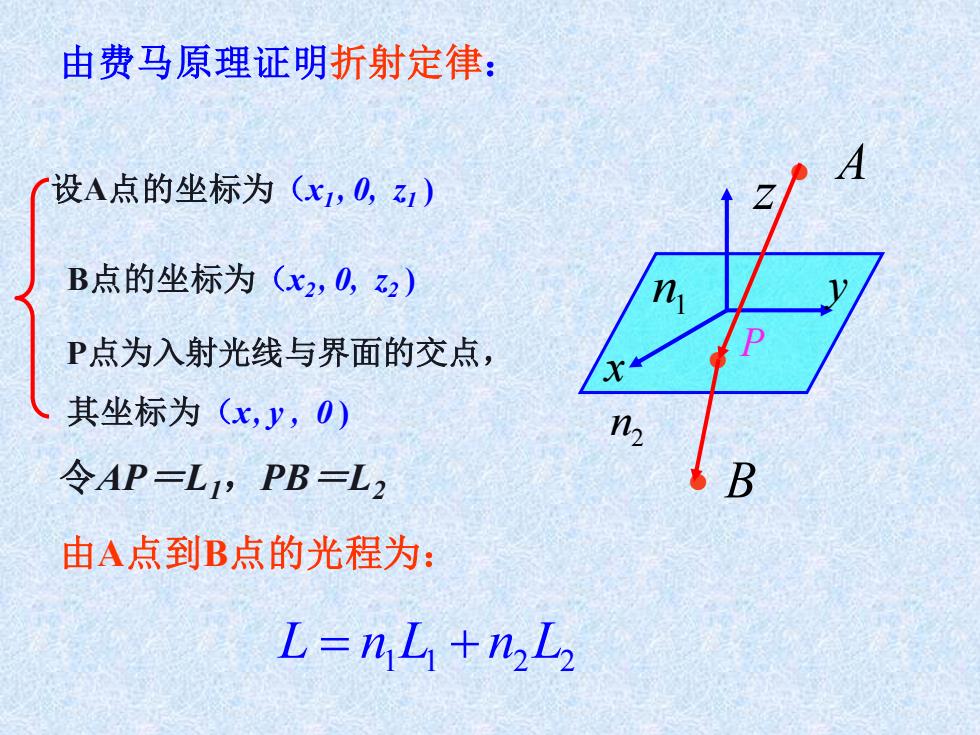
由费马原理证明折射定律: x y z n1 n2 • A • B • P 设A点的坐标为(x1 , 0, z1 ) B点的坐标为(x2 , 0, z2 ) P点为入射光线与界面的交点, 其坐标为(x, y , 0 ) 令AP=L1,PB=L2 由A点到B点的光程为: L = n1 L1 + n2 L2

凸=(x-x)}+y2+ L2=0-x)+y2+ 根据费马原理 δL=0 即 8(nL+nl)=0 8 (m,4+nm,)=0 ay 分别将L和L2代入上式可得: 急w+w小-+ 2-0 (1) LL
2 1 2 2 1 1 L = (x − x ) + y + z 2 2 2 2 2 2 L = (x − x ) + y + z 根据费马原理 L = 0 即 ( ) 0 1 1 + 2 2 = n L n L x ( 1 1 + 2 2 ) = 0 n L n L y 分别将L1和L2代入上式可得: ( ) 0 (1) 2 2 1 1 1 1 + 2 2 = + = L n y L n y n L n L y